INVOEGING IN EEN AVL-BOOM

AVL-boom:

AVL-boom is een zelfbalancerende binaire zoekboom ( BST ) waarbij het verschil tussen de hoogten van de linker- en rechtersubboom niet groter kan zijn dan een voor alle knooppunten.

Voorbeeld van AVL-boom:

De bovenstaande boom is AVL omdat de verschillen tussen de hoogten van de linker en rechter subboom voor elk knooppunt kleiner dan of gelijk zijn aan 1.

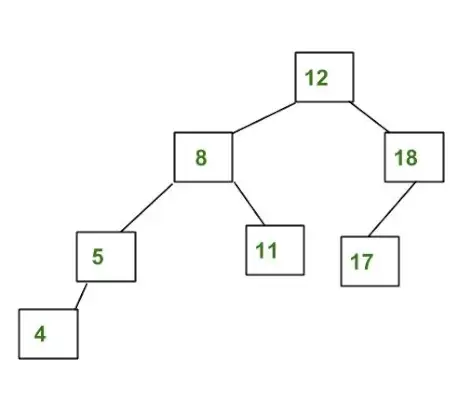
Voorbeeld van een boom die GEEN AVL-boom is:

De bovenstaande boom is geen AVL omdat de verschillen tussen de hoogten van de linker en rechter deelboom voor 8 en 12 groter zijn dan 1.

Waarom AVL-bomen?

De meeste BST-bewerkingen (bijvoorbeeld zoeken, max, min, invoegen, verwijderen.. enz.) duren Oh) tijd waar H is de hoogte van de BST. De kosten van deze operaties kunnen stijgen Op) voor een scheve binaire boom . Als we ervoor zorgen dat de hoogte van de boom behouden blijft O(logboek(n)) na elke invoeging en verwijdering, dan kunnen we een bovengrens garanderen van O(logboek(n)) voor al deze operaties. De hoogte van een AVL-boom is altijd O(logboek(n)) waar N is het aantal knooppunten in de boom.

Plaatsing in AVL-boom:

Om ervoor te zorgen dat de gegeven boom na elke invoeging AVL blijft, moeten we de standaard BST-invoegbewerking uitbreiden om wat herbalancering uit te voeren.
Hieronder volgen twee basisbewerkingen die kunnen worden uitgevoerd om een BST in evenwicht te brengen zonder de BST-eigenschap te schenden (toetsen (links)

Linksom draaien
Rechtse rotatie

T1, T2 and T3 are subtrees of the tree, rooted with y (on the left side) or x (on the right side) y x /  Right Rotation /  x T3 - - - - - - ->T1 en / <- - - - - - - /  T1 T2 Left Rotation T2 T3 Keys in both of the above trees follow the following order keys(T1) < key(x) < keys(T2) < key(y) < keys(T3) So BST property is not violated anywhere.>

Aanbevolen praktijk AVL-boom inbrengen Probeer het!

Te volgen stappen voor het inbrengen:

Laat het nieuw ingevoegde knooppunt dat zijn In

Standaard uitvoeren BST invoegen voor In .
Beginnend vanaf In , reis naar boven en vind de eerste ongebalanceerd knooppunt . Laten Met wees het eerste ongebalanceerde knooppunt, En wees de kind van Met die op het pad vandaan komt In naar Met En X wees de kleinkind van Met die op het pad vandaan komt In naar Met .
Breng de boom opnieuw in evenwicht door de juiste rotaties uit te voeren op de subboom waarmee hij is geworteld Met. Er kunnen vier mogelijke gevallen zijn die moeten worden afgehandeld x,y En Met kan op 4 manieren worden gerangschikt.
Hieronder volgen de mogelijke 4 arrangementen:
- y is het linkerkind van z en x is het linkerkind van y (linker linkergeval)
- y is het linkerkind van z en x is het rechterkind van y (linker-rechtsgeval)
- y is het rechterkind van z en x is het rechterkind van y (Right Right Case)
- y is het rechterkind van z en x is het linkerkind van y (rechts-links geval)

Hieronder volgen de handelingen die in de bovengenoemde vier gevallen moeten worden uitgevoerd. In alle gevallen hoeven we dat alleen maar te doen opnieuw in evenwicht brengen de subboom waarmee geworteld is Met en de volledige boom wordt in evenwicht naarmate de hoogte van de deelboom (na de juiste rotaties) verankerd is Met wordt hetzelfde als vóór het inbrengen.

1. Linker linkerbehuizing

T1, T2, T3 and T4 are subtrees. z y /  /  y T4 Right Rotate (z) x z /  - - - - - - - - ->/  /  x T3 T1 T2 T3 T4 /  T1 T2>

2. Links-rechts behuizing

 z z x /  /  /  y T4 Left Rotate (y) x T4 Right Rotate(z) y z /  - - - - - - - - ->/  - - - - - - - -> /  /  T1 x y T3 T1 T2 T3 T4 /  /  T2 T3 T1 T2>

3. Rechts Rechts hoesje

 z y /  /  T1 y Left Rotate(z) z x /  - - - - - - - ->/  /  T2 x T1 T2 T3 T4 /  T3 T4>

4. Rechts-links behuizing

 z z x /  /  /  T1 y Right Rotate (y) T1 x Left Rotate(z) z y /  - - - - - - - - ->/  - - - - - - - -> /  /  x T4 T2 y T1 T2 T3 T4 /  /  T2 T3 T3 T4>

Illustratie van invoeging bij AVL-boom

ontlensd1

avlinsert2-jpg

avlinsert3

avlinsert4

avlinsert5

Benadering:

Het idee is om recursieve BST-invoeging te gebruiken. Na het invoegen krijgen we één voor één verwijzingen naar alle voorouders op een bottom-up manier. We hebben dus geen ouderwijzer nodig om naar boven te reizen. De recursieve code zelf reist omhoog en bezoekt alle voorouders van het nieuw ingevoegde knooppunt.

Volg de onderstaande stappen om het idee te implementeren:

Voer het normale uit BST-invoeging.
Het huidige knooppunt moet een van de voorouders zijn van het nieuw ingevoegde knooppunt. Update de hoogte van het huidige knooppunt.
Verkrijg de balansfactor (hoogte linker subboom – hoogte rechter subboom) van het huidige knooppunt.
Als de balansfactor groter is dan 1, dan is het huidige knooppunt uit balans en bevinden we ons in de Links Links geval of links Rechts geval . Om te controleren of dat zo is linker linker geval of niet, vergelijk de nieuw ingestoken sleutel met de sleutel in de linker subboomwortel .
Als de balansfactor kleiner is dan -1 , dan is het huidige knooppunt uit balans en bevinden we ons in het geval Rechts-Rechts of Rechts-Links. Om te controleren of dit het juiste geval is of niet, vergelijkt u de nieuw ingevoegde sleutel met de sleutel in de rechter subboomwortel.

Hieronder vindt u de implementatie van de bovenstaande aanpak:

C++14

// C++ program to insert a node in AVL tree> #include> using> namespace> std;> > // An AVL tree node> class> Node> {> >public>:> >int> key;> >Node *left;> >Node *right;> >int> height;> };> > // A utility function to get the> // height of the tree> int> height(Node *N)> {> >if> (N == NULL)> >return> 0;> >return> N->hoogte;> }> > // A utility function to get maximum> // of two integers> int> max(>int> a,>int> b)> {> >return> (a>B)? a: b;> }> > /* Helper function that allocates a> >new node with the given key and> >NULL left and right pointers. */> Node* newNode(>int> key)> {> >Node* node =>new> Node();> >node->sleutel = sleutel;> >node->links = NULL;> >node->rechts = NULL;> >node->hoogte = 1;>// new node is initially> >// added at leaf> >return>(node);> }> > // A utility function to right> // rotate subtree rooted with y> // See the diagram given above.> Node *rightRotate(Node *y)> {> >Node *x = y->links;> >Node *T2 = x->rechts;> > >// Perform rotation> >x->rechts = y;> >y->links = T2;> > >// Update heights> >y->hoogte = max(hoogte(y->links),> >height(y->rechts)) + 1;> >x->hoogte = max(hoogte(x->links),> >height(x->rechts)) + 1;> > >// Return new root> >return> x;> }> > // A utility function to left> // rotate subtree rooted with x> // See the diagram given above.> Node *leftRotate(Node *x)> {> >Node *y = x->rechts;> >Node *T2 = y->links;> > >// Perform rotation> >y->links = x;> >x->rechts = T2;> > >// Update heights> >x->hoogte = max(hoogte(x->links),> >height(x->rechts)) + 1;> >y->hoogte = max(hoogte(y->links),> >height(y->rechts)) + 1;> > >// Return new root> >return> y;> }> > // Get Balance factor of node N> int> getBalance(Node *N)> {> >if> (N == NULL)> >return> 0;> >return> height(N->links) - hoogte(N->rechts);> }> > // Recursive function to insert a key> // in the subtree rooted with node and> // returns the new root of the subtree.> Node* insert(Node* node,>int> key)> {> >/* 1. Perform the normal BST insertion */> >if> (node == NULL)> >return>(newNode(key));> > >if> (key key)> >node->links = invoegen(knooppunt->links, sleutel);> >else> if> (key>knooppunt->sleutel)> >node->rechts = invoegen(knooppunt->rechts, sleutel);> >else> // Equal keys are not allowed in BST> >return> node;> > >/* 2. Update height of this ancestor node */> >node->hoogte = 1 + max(hoogte(knooppunt->links),> >height(node->rechts));> > >/* 3. Get the balance factor of this ancestor> >node to check whether this node became> >unbalanced */> >int> balance = getBalance(node);> > >// If this node becomes unbalanced, then> >// there are 4 cases> > >// Left Left Case> >if> (balance>1 &&-toets links->toets)> >return> rightRotate(node);> > >// Right Right Case> >if> (balance node->rechter->toets)> >return> leftRotate(node);> > >// Left Right Case> >if> (balance>1 && toets> knooppunt->links->toets)> >{> >node->links = linksRoteren(knooppunt->links);> >return> rightRotate(node);> >}> > >// Right Left Case> >if> (balance <-1 && key right->toets)> >{> >node->rechts = rechtsRoteren(knooppunt->rechts);> >return> leftRotate(node);> >}> > >/* return the (unchanged) node pointer */> >return> node;> }> > // A utility function to print preorder> // traversal of the tree.> // The function also prints height> // of every node> void> preOrder(Node *root)> {> >if>(root != NULL)> >{> >

cout ' ';   preOrder(root->links);   preOrder(root->rechts);   } } // Stuurprogrammacode int main() { Knooppunt *root = NULL;     /* Boom construeren zoals weergegeven in de bovenstaande afbeelding */ root = insert(root, 10);   wortel = invoegen(wortel, 20);   wortel = invoegen(wortel, 30);   wortel = invoegen(wortel, 40);   wortel = invoegen(wortel, 50);   wortel = invoegen(wortel, 25);     /* De geconstrueerde AVL-boom zou 30 /  20 40 /   10 25 50 */ cout zijn<< 'Preorder traversal of the '  'constructed AVL tree is 
';   preOrder(root);     return 0;  }    // This code is contributed by  // rathbhupendra>

C

// C program to insert a node in AVL tree> #include> #include> > // An AVL tree node> struct> Node> {> >int> key;> >struct> Node *left;> >struct> Node *right;> >int> height;> };> > // A utility function to get the height of the tree> int> height(>struct> Node *N)> {> >if> (N == NULL)> >return> 0;> >return> N->hoogte;> }> > // A utility function to get maximum of two integers> int> max(>int> a,>int> b)> {> >return> (a>B)? a: b;> }> > /* Helper function that allocates a new node with the given key and> >NULL left and right pointers. */> struct> Node* newNode(>int> key)> {> >struct> Node* node = (>struct> Node*)> >malloc>(>sizeof>(>struct> Node));> >node->sleutel = sleutel;> >node->links = NULL;> >node->rechts = NULL;> >node->hoogte = 1;>// new node is initially added at leaf> >return>(node);> }> > // A utility function to right rotate subtree rooted with y> // See the diagram given above.> struct> Node *rightRotate(>struct> Node *y)> {> >struct> Node *x = y->links;> >struct> Node *T2 = x->rechts;> > >// Perform rotation> >x->rechts = y;> >y->links = T2;> > >// Update heights> >y->hoogte = max(hoogte(y->links),> >height(y->rechts)) + 1;> >x->hoogte = max(hoogte(x->links),> >height(x->rechts)) + 1;> > >// Return new root> >return> x;> }> > // A utility function to left rotate subtree rooted with x> // See the diagram given above.> struct> Node *leftRotate(>struct> Node *x)> {> >struct> Node *y = x->rechts;> >struct> Node *T2 = y->links;> > >// Perform rotation> >y->links = x;> >x->rechts = T2;> > >// Update heights> >x->hoogte = max(hoogte(x->links),> >height(x->rechts)) + 1;> >y->hoogte = max(hoogte(y->links),> >height(y->rechts)) + 1;> > >// Return new root> >return> y;> }> > // Get Balance factor of node N> int> getBalance(>struct> Node *N)> {> >if> (N == NULL)> >return> 0;> >return> height(N->links) - hoogte(N->rechts);> }> > // Recursive function to insert a key in the subtree rooted> // with node and returns the new root of the subtree.> struct> Node* insert(>struct> Node* node,>int> key)> {> >/* 1. Perform the normal BST insertion */> >if> (node == NULL)> >return>(newNode(key));> > >if> (key key)> >node->links = invoegen(knooppunt->links, sleutel);> >else> if> (key>knooppunt->sleutel)> >node->rechts = invoegen(knooppunt->rechts, sleutel);> >else> // Equal keys are not allowed in BST> >return> node;> > >/* 2. Update height of this ancestor node */> >node->hoogte = 1 + max(hoogte(knooppunt->links),> >height(node->rechts));> > >/* 3. Get the balance factor of this ancestor> >node to check whether this node became> >unbalanced */> >int> balance = getBalance(node);> > >// If this node becomes unbalanced, then> >// there are 4 cases> > >// Left Left Case> >if> (balance>1 &&-toets links->toets)> >return> rightRotate(node);> > >// Right Right Case> >if> (balance node->rechter->toets)> >return> leftRotate(node);> > >// Left Right Case> >if> (balance>1 && toets> knooppunt->links->toets)> >{> >node->links = linksRoteren(knooppunt->links);> >return> rightRotate(node);> >}> > >// Right Left Case> >if> (balance <-1 && key right->toets)> >{> >node->rechts = rechtsRoteren(knooppunt->rechts);> >return> leftRotate(node);> >}> > >/* return the (unchanged) node pointer */> >return> node;> }> > // A utility function to print preorder traversal> // of the tree.> // The function also prints height of every node> void> preOrder(>struct> Node *root)> {> >if>(root != NULL)> >{> >printf>(>'%d '>, root->sleutel);> >preOrder(root->links);> >preOrder(root->rechts);> >}> }> > /* Driver program to test above function*/> int> main()> {> >struct> Node *root = NULL;> > >/* Constructing tree given in the above figure */> >root = insert(root, 10);> >root = insert(root, 20);> >root = insert(root, 30);> >root = insert(root, 40);> >root = insert(root, 50);> >root = insert(root, 25);> > >/* The constructed AVL Tree would be> >30> >/> >20 40> >/> >10 25 50> >*/> > >printf>(>'Preorder traversal of the constructed AVL'> >

' tree is 
'>

);> >preOrder(root);> > >return> 0;> }>

Java

// Java program for insertion in AVL Tree> class> Node {> >int> key, height;> >Node left, right;> > >Node(>int> d) {> >key = d;> >height =>1>;> >}> }> > class> AVLTree {> > >Node root;> > >// A utility function to get the height of the tree> >int> height(Node N) {> >if> (N ==>null>)> >return> 0>;> > >return> N.height;> >}> > >// A utility function to get maximum of two integers> >int> max(>int> a,>int> b) {> >return> (a>B) ? a: b;> >}> > >// A utility function to right rotate subtree rooted with y> >// See the diagram given above.> >Node rightRotate(Node y) {> >Node x = y.left;> >Node T2 = x.right;> > >// Perform rotation> >x.right = y;> >y.left = T2;> > >// Update heights> >y.height = max(height(y.left), height(y.right)) +>1>;> >x.height = max(height(x.left), height(x.right)) +>1>;> > >// Return new root> >return> x;> >}> > >// A utility function to left rotate subtree rooted with x> >// See the diagram given above.> >Node leftRotate(Node x) {> >Node y = x.right;> >Node T2 = y.left;> > >// Perform rotation> >y.left = x;> >x.right = T2;> > >// Update heights> >x.height = max(height(x.left), height(x.right)) +>1>;> >y.height = max(height(y.left), height(y.right)) +>1>;> > >// Return new root> >return> y;> >}> > >// Get Balance factor of node N> >int> getBalance(Node N) {> >if> (N ==>null>)> >return> 0>;> > >return> height(N.left) - height(N.right);> >}> > >Node insert(Node node,>int> key) {> > >/* 1. Perform the normal BST insertion */> >if> (node ==>null>)> >return> (>new> Node(key));> > >if>

(key   node.left = insert(node.left, key);   else if (key>knooppunt.sleutel) knooppunt.rechts = invoegen(knooppunt.rechts, sleutel);   else // Dubbele sleutels niet toegestaan retourknooppunt;     /* 2. Hoogte van dit bovenliggende knooppunt bijwerken */ node.height = 1 + max(height(node.left), height(node.right));     /* 3. Haal de balansfactor van dit bovenliggende knooppunt op om te controleren of dit knooppunt uit balans is geraakt */ int balance = getBalance(node);     // Als dit knooppunt uit balans raakt, zijn er 4 gevallen. Left Left Case if (saldo> 1 && key return rightRotate(node); // Right Right Case if (saldo<-1 && key>knooppunt.right.key) return leftRotate(knooppunt);     // Links Rechts Case if (saldo> 1 && sleutel> node.left.key) { node.left = leftRotate(node.left);   retour rechtsRoteren(knooppunt);   } // Rechts Links Case if (balance<-1 && key   node.right = rightRotate(node.right);   return leftRotate(node);   }     /* return the (unchanged) node pointer */  return node;   }     // A utility function to print preorder traversal   // of the tree.   // The function also prints height of every node   void preOrder(Node node) {   if (node != null) {   System.out.print(node.key + ' ');   preOrder(node.left);   preOrder(node.right);   }   }     public static void main(String[] args) {   AVLTree tree = new AVLTree();     /* Constructing tree given in the above figure */  tree.root = tree.insert(tree.root, 10);   tree.root = tree.insert(tree.root, 20);   tree.root = tree.insert(tree.root, 30);   tree.root = tree.insert(tree.root, 40);   tree.root = tree.insert(tree.root, 50);   tree.root = tree.insert(tree.root, 25);     /* The constructed AVL Tree would be   30   /    20 40   /     10 25 50   */  System.out.println('Preorder traversal' +   ' of constructed tree is : ');   tree.preOrder(tree.root);   }  }  // This code has been contributed by Mayank Jaiswal>

Python3

# Python code to insert a node in AVL tree> > # Generic tree node class> class> TreeNode(>object>):> >def> __init__(>self>, val):> >self>.val>=> val> >self>.left>=> None> >self>.right>=> None> >self>.height>=> 1> > # AVL tree class which supports the> # Insert operation> class> AVL_Tree(>object>):> > ># Recursive function to insert key in> ># subtree rooted with node and returns> ># new root of subtree.> >def> insert(>self>, root, key):> > ># Step 1 - Perform normal BST> >if> not> root:> >return> TreeNode(key)> >elif>

key   root.left = self.insert(root.left, key)   else:   root.right = self.insert(root.right, key)     # Step 2 - Update the height of the   # ancestor node   root.height = 1 + max(self.getHeight(root.left),   self.getHeight(root.right))     # Step 3 - Get the balance factor   balance = self.getBalance(root)     # Step 4 - If the node is unbalanced,   # then try out the 4 cases   # Case 1 - Left Left   if balance>1 en sleutel return self.rightRotate(root) # Geval 2 - Rechts Rechts als evenwicht<-1 and key>root.right.val: return self.leftRotate(root) # Geval 3 - Links Rechts als balans> 1 en sleutel> root.left.val: root.left = self.leftRotate(root.left) retourneert self.rightRotate(root ) # Geval 4 - Rechts Links als evenwicht<-1 and key   root.right = self.rightRotate(root.right)   return self.leftRotate(root)     return root     def leftRotate(self, z):     y = z.right   T2 = y.left     # Perform rotation   y.left = z   z.right = T2     # Update heights   z.height = 1 + max(self.getHeight(z.left),   self.getHeight(z.right))   y.height = 1 + max(self.getHeight(y.left),   self.getHeight(y.right))     # Return the new root   return y     def rightRotate(self, z):     y = z.left   T3 = y.right     # Perform rotation   y.right = z   z.left = T3     # Update heights   z.height = 1 + max(self.getHeight(z.left),   self.getHeight(z.right))   y.height = 1 + max(self.getHeight(y.left),   self.getHeight(y.right))     # Return the new root   return y     def getHeight(self, root):   if not root:   return 0    return root.height     def getBalance(self, root):   if not root:   return 0    return self.getHeight(root.left) - self.getHeight(root.right)     def preOrder(self, root):     if not root:   return    print('{0} '.format(root.val), end='')   self.preOrder(root.left)   self.preOrder(root.right)      # Driver program to test above function  myTree = AVL_Tree()  root = None   root = myTree.insert(root, 10)  root = myTree.insert(root, 20)  root = myTree.insert(root, 30)  root = myTree.insert(root, 40)  root = myTree.insert(root, 50)  root = myTree.insert(root, 25)    '''The constructed AVL Tree would be   30   /    20 40   /     10 25 50'''   # Preorder Traversal  print('Preorder traversal of the',   'constructed AVL tree is')  myTree.preOrder(root)  print()    # This code is contributed by Ajitesh Pathak>

C#

// C# program for insertion in AVL Tree> using> System;> > class> Node> {> >public> int> key, height;> >public> Node left, right;> > >public> Node(>int> d)> >{> >key = d;> >height = 1;> >}> }> > public> class> AVLTree> {> > >Node root;> > >// A utility function to get> >// the height of the tree> >int> height(Node N)> >{> >if> (N ==>null>)> >return> 0;> > >return> N.height;> >}> > >// A utility function to get> >// maximum of two integers> >int> max(>int> a,>int> b)> >{> >return> (a>B) ? a: b;> >}> > >// A utility function to right> >// rotate subtree rooted with y> >// See the diagram given above.> >Node rightRotate(Node y)> >{> >Node x = y.left;> >Node T2 = x.right;> > >// Perform rotation> >x.right = y;> >y.left = T2;> > >// Update heights> >y.height = max(height(y.left),> >height(y.right)) + 1;> >x.height = max(height(x.left),> >height(x.right)) + 1;> > >// Return new root> >return> x;> >}> > >// A utility function to left> >// rotate subtree rooted with x> >// See the diagram given above.> >Node leftRotate(Node x)> >{> >Node y = x.right;> >Node T2 = y.left;> > >// Perform rotation> >y.left = x;> >x.right = T2;> > >// Update heights> >x.height = max(height(x.left),> >height(x.right)) + 1;> >y.height = max(height(y.left),> >height(y.right)) + 1;> > >// Return new root> >return> y;> >}> > >// Get Balance factor of node N> >int> getBalance(Node N)> >{> >if> (N ==>null>)> >return> 0;> > >return> height(N.left) - height(N.right);> >}> > >Node insert(Node node,>int> key)> >{> > >/* 1. Perform the normal BST insertion */> >if> (node ==>null>)> >return> (>new> Node(key));> > >if>

(key   node.left = insert(node.left, key);   else if (key>knooppunt.sleutel) knooppunt.rechts = invoegen(knooppunt.rechts, sleutel);   else // Dubbele sleutels niet toegestaan retourknooppunt;     /* 2. Hoogte van dit bovenliggende knooppunt bijwerken */ node.height = 1 + max(height(node.left), height(node.right));     /* 3. Haal de balansfactor van dit bovenliggende knooppunt op om te controleren of dit knooppunt uit balans is geraakt */ int balance = getBalance(node);     // Als dit knooppunt uit balans raakt, zijn er 4 gevallen Left Left Case if (saldo> 1 && key return rightRotate(node); // Right Right Case if (balance node.right.key) return leftRotate(node) ; // Links Rechts Case if (saldo> 1 && sleutel> node.left.key) { node.left = leftRotate(node.left); return rightRotate(node } // Rechts Links Case if (saldo);<-1 && key < node.right.key)   {   node.right = rightRotate(node.right);   return leftRotate(node);   }     /* return the (unchanged) node pointer */  return node;   }     // A utility function to print preorder traversal   // of the tree.   // The function also prints height of every node   void preOrder(Node node)   {   if (node != null)   {   Console.Write(node.key + ' ');   preOrder(node.left);   preOrder(node.right);   }   }     // Driver code   public static void Main(String[] args)   {   AVLTree tree = new AVLTree();     /* Constructing tree given in the above figure */  tree.root = tree.insert(tree.root, 10);   tree.root = tree.insert(tree.root, 20);   tree.root = tree.insert(tree.root, 30);   tree.root = tree.insert(tree.root, 40);   tree.root = tree.insert(tree.root, 50);   tree.root = tree.insert(tree.root, 25);     /* The constructed AVL Tree would be   30   /    20 40   /     10 25 50   */  Console.Write('Preorder traversal' +   ' of constructed tree is : ');   tree.preOrder(tree.root);   }  }    // This code has been contributed  // by PrinciRaj1992>

Javascript

> > >// JavaScript program for insertion in AVL Tree> >class Node {> >constructor(d) {> >this>.key = d;> >this>.height = 1;> >this>.left =>null>;> >this>.right =>null>;> >}> >}> > >class AVLTree {> >constructor() {> >this>.root =>null>;> >}> > >// A utility function to get> >// the height of the tree> >height(N) {> >if> (N ==>null>)>return> 0;> > >return> N.height;> >}> > >// A utility function to get> >// maximum of two integers> >max(a, b) {> >return> a>B ? a: b;> >}> > >// A utility function to right> >// rotate subtree rooted with y> >// See the diagram given above.> >rightRotate(y) {> >var> x = y.left;> >var> T2 = x.right;> > >// Perform rotation> >x.right = y;> >y.left = T2;> > >// Update heights> >y.height =>this>.max(>this>.height(y.left),> >this>.height(y.right)) + 1;> >x.height =>this>.max(>this>.height(x.left),> >this>.height(x.right)) + 1;> > >// Return new root> >return> x;> >}> > >// A utility function to left> >// rotate subtree rooted with x> >// See the diagram given above.> >leftRotate(x) {> >var> y = x.right;> >var> T2 = y.left;> > >// Perform rotation> >y.left = x;> >x.right = T2;> > >// Update heights> >x.height =>this>.max(>this>.height(x.left),> >this>.height(x.right)) + 1;> >y.height =>this>.max(>this>.height(y.left),> >this>.height(y.right)) + 1;> > >// Return new root> >return> y;> >}> > >// Get Balance factor of node N> >getBalance(N) {> >if> (N ==>null>)>return> 0;> > >return> this>.height(N.left) ->this>.height(N.right);> >}> > >insert(node, key) {> >/* 1. Perform the normal BST insertion */> >if> (node ==>null>)>return> new> Node(key);> > >if>

(key   node.left = this.insert(node.left, key);   else if (key>knooppunt.sleutel) knooppunt.rechts = dit.insert(knooppunt.rechts, sleutel);   // Dubbele sleutels niet toegestaan, anders retourknooppunt;     /* 2. Hoogte van dit bovenliggende knooppunt bijwerken */ node.height = 1 + this.max(this.height(node.left), this.height(node.right));     /* 3. Haal de balansfactor van dit bovenliggende knooppunt op om te controleren of dit knooppunt uit balans is geraakt */ var balance = this.getBalance(node);     // Als dit knooppunt uit balans raakt, zijn er 4 gevallen. Left Left Case if (balance> 1 && key return this.rightRotate(node); // Right Right Case if (balance node.right.key) retourneert dit. leftRotate(node); // Left Right Case if (saldo> 1 && key> node.left.key) {node.left = this.leftRotate(node.left); Linkerkast als (saldo<-1 && key < node.right.key) {   node.right = this.rightRotate(node.right);   return this.leftRotate(node);   }     /* return the (unchanged) node pointer */  return node;   }     // A utility function to print preorder traversal   // of the tree.   // The function also prints height of every node   preOrder(node) {   if (node != null) {   document.write(node.key + ' ');   this.preOrder(node.left);   this.preOrder(node.right);   }   }   }   // Driver code   var tree = new AVLTree();     /* Constructing tree given in the above figure */  tree.root = tree.insert(tree.root, 10);   tree.root = tree.insert(tree.root, 20);   tree.root = tree.insert(tree.root, 30);   tree.root = tree.insert(tree.root, 40);   tree.root = tree.insert(tree.root, 50);   tree.root = tree.insert(tree.root, 25);     /* The constructed AVL Tree would be   30   /    20 40   /     10 25 50   */  document.write(   'Preorder traversal of the ' + 'constructed AVL tree is '  );   tree.preOrder(tree.root);>

Uitvoer

Preorder traversal of the constructed AVL tree is 30 20 10 25 40 50>

Complexiteitsanalyse

Tijdcomplexiteit: O(log(n)), voor invoeging
Hulpruimte: O(1)

Java-programmeerarrays

De rotatiebewerkingen (links en rechts draaien) nemen een constante tijd in beslag omdat daar slechts een paar wijzers worden gewijzigd. Het bijwerken van de hoogte en het verkrijgen van de balansfactor kost ook constante tijd. De tijdscomplexiteit van de AVL-insert blijft dus hetzelfde als die van de BST-insertie, die O(h) is, waarbij h de hoogte van de boom is. Omdat de AVL-boom in balans is, is de hoogte O(Logn). De tijdscomplexiteit van AVL-insert is dus O(Logn).

Vergelijking met roodzwarte boom:

De AVL-boom en andere zelfbalancerende zoekbomen zoals Red Black zijn handig om alle basisbewerkingen in O(log n)-tijd uit te voeren. De AVL-bomen zijn evenwichtiger dan rood-zwarte bomen, maar kunnen tijdens het inbrengen en verwijderen meer rotaties veroorzaken. Dus als uw toepassing veel frequente invoegingen en verwijderingen omvat, dan verdient Rood-Zwarte bomen de voorkeur. En als de invoegingen en verwijderingen minder frequent voorkomen en zoeken de frequentere bewerking is, dan verdient de AVL-boom de voorkeur boven Red Black Tree.

Hieronder volgt het bericht dat moet worden verwijderd in AVL Tree:
AVL-boom | Set 2 (verwijdering)

TechCodeview