In het midden van een driehoek is het snijpunt van alle drie de deellijnen van een driehoek. Het middenpunt is een belangrijk punt in een driehoek waar lijnen die de hoeken doormidden snijden, samenkomen. Dit punt is ook het middelpunt van een cirkel genaamd Incircle, die perfect in de driehoek past en alle drie de zijden op dezelfde manier raakt. Dit artikel behandelt verschillende concepten van het middelpunt van de driehoek, zoals waarom dit punt belangrijk is, hoe je het kunt vinden met behulp van een kompas of cijfers, en eigenschappen van het middelpunt van de cirkel.

Inhoudsopgave

• Wat is het middelpunt van een driehoek?
• Eigenschappen van een incenter van een driehoek
• In het midden van een driehoeksformule
• Hoe het middelpunt van een driehoek te vinden
• Centroid, Circumcenter, Incenter, Orthocenter

Wat is het middelpunt van een driehoek?

Het middelpunt van een driehoek is, zoals de naam al doet vermoeden, het middelpunt van de driehoek. Dit punt, dat we een incenter noemen, vormt op de kruising waar alle lijnen die de binnenhoeken doorsnijden samenkomen. De afstand van het punt tot alle drie de zijden van de driehoek is hetzelfde. De ingeschreven cirkel van de driehoek past ook op een perfecte cirkel binnen de driehoek en deze cirkel wordt de ingeschreven cirkel van de driehoek genoemd.

Incenter-definitie

Het middelpunt van een driehoek is het punt binnen de driehoek waar alle drie de lijnen die de binnenhoeken doormidden snijden, samenkomen. Dit punt ligt op dezelfde afstand van de drie zijden van de driehoek, waardoor het lijkt op het midden van de driehoek. Het is ook het middelpunt van de grootste cirkel die precies in de driehoek past, die we de ingeschreven cirkel noemen. Om het centrum te symboliseren, gebruiken we meestal de letter I,

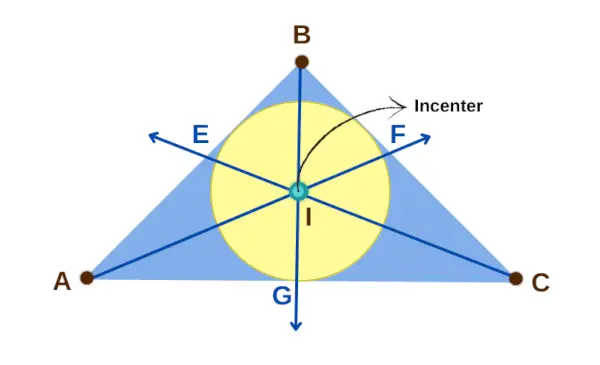
In het midden van een driehoek

Eigenschappen van een incenter van een driehoek

Enkele belangrijke eigenschappen van het middelpunt van de driehoek worden hieronder gegeven:

Eigenschap 1: Als I het middelpunt is van een driehoek ABC, dan zijn drie paar lijnsegmenten even lang: AE en AG, CG en CF, en BF en BE. Dit betekent dat AE = AG, CG = CF en BF = BE.

Eigenschap 2: Het centrum I heeft ook een bijzondere relatie met de hoeken van de driehoek. Het zorgt ervoor dat de hoeken ∠BAI en ∠CAI gelijk zijn, ∠BCI en ∠ACI gelijk zijn, en ∠ABI en ∠CBI gelijk zijn. Dit volgt de bissectricestelling.

Eigenschap 3: Het centrum I is het middelpunt van een cirkel die alle drie de zijden van de driehoek raakt, en de afstanden daarvan I de zijden van de driehoek (EI, FI, GI) zijn allemaal hetzelfde. Deze afstanden worden de inradii of de straal van de incircle genoemd.

Eigenschap 4: Je kunt de oppervlakte van de driehoek berekenen met behulp van de halve omtrek (s) en de inradius (r). De formule is A = sr, waarbij A de oppervlakte is, s de halve omtrek (s = (a + b + c)/2, waarbij a, b en c de zijdelengten van de driehoek zijn), en r de lengte van de zijden is. binnenstraal.

Eigenschap 5: Het middelpunt van een driehoek blijft altijd binnen de driehoek. In tegenstelling tot het orthocentrum, dat zich in sommige gevallen buiten de driehoek kan bevinden, bevindt het incenter zich altijd binnen de grenzen van de driehoek.

chmod 755

In het centrum van een driehoeksformule

De formule om het middelpunt van de formule te vinden met 3 coördinaten (x₁, En₁), (X₂, En₂), en (x₃, En₃) is:

{(bijl ₁ + bx ₂ + cx ₃ )/(a + b + c), (is ₁ + door ₂ + c ₃ )/(a + b + c)}

In eenvoudige bewoordingen: om de essentie te begrijpen, moet u:

• Vermenigvuldig de x-coördinaat van punt A met zijdelengte a, de x-coördinaat van punt B met zijdelengte b, en de x-coördinaat van punt C met zijdelengte c. Voeg deze vervolgens samen.
• Deel het resultaat door de som van de zijdelengten a, b en c.
• Herhaal hetzelfde proces voor de y-coördinaten, maar gebruik de zijdelengtes a, b en c.

Incenter van een driehoekshoekformule

De formule om het middelpunt van een hoek van een driehoek te vinden is als volgt:

Stel dat in een driehoek D, F en G de punten zijn waar de deelloodlijnen van respectievelijk de hoeken A, B en C de zijden BC, AC en AB ontmoeten.

De hoek ∠AIB (waarbij I het middelpunt van de driehoek is) kan worden berekend met behulp van de formule:

∠AIB = 180° – (de helft van de som van de hoeken A en B)

OF

∠AIB = 180° – (∠A + ∠B)/2

Hoe het middelpunt van een driehoek te vinden

Er zijn twee methoden om het middelpunt van een driehoek te vinden. In de constructie lokaliseren we het incenter door de deellijnen van de driehoek te tekenen. Bij coördinatengeometrie gebruiken we een formule om het incenter te bepalen.

Coördinaatgeometrie gebruiken : Zoek het middelpunt van de driehoek met de coördinaten gegeven als: A(2, 2), B(6, 2) en C(4, 5)

Volgens de gegeven informatie

• (X₁, En₁) = (2, 2)
• (X₂, En₂) = (6, 2)
• (X₃, En₃) = (4, 5)

We weten dat het middelpunt van een driehoek is:

ik(x,y) = {(bijl ₁ + bx ₂ + cx ₃ )/(a + b + c), (is ₁ + door ₂ + c ₃ )/(a + b + c)}

Voor zijde a: De afstand tussen punten B en C = √((6 – 4)²+ (2 – 5)²) = √8

Voor zijde b: De afstand tussen punten A en C = √((2 – 4)²+ (2 – 5)²) = √13

Voor zijde c: De afstand tussen punten A en B = √((6 – 2)²+ (2 – 2)²) = 4

Als we de waarden van a, b, c in de formule van incenter plaatsen, krijgen we:

wanneer werd de school uitgevonden?

I(x, y) = {(8×2 + 13×5 + 4×4)/(8 + 13 +4), (8×2 + 13×2 + 4×5)/(8 + 13 +4 )}

⇒ Ik(x, y) = (16 + 78 + 16)/(25), (16 + 26 + 20)/(25)

⇒ Ik(x, y) = (110/25, 62/25) = (22/5,62/25)

∴ Het middelpunt van de driehoek ABC met de coördinaten is (22/5,62/25)

Hoe construeer je het middelpunt van een driehoek?

Om het middelpunt van een driehoek te construeren, heb je een kompas nodig. Gebruik een kompas en volg de onderstaande stappen:

Stap 1: Plaats het ene uiteinde van het kompas op een hoekpunt van de driehoek en het andere uiteinde raakt één kant.

Stap 2: Gebruik het kompas om twee bogen aan twee zijden van de driehoek te tekenen.

Stap 3: Maak met dezelfde afstand op het kompas twee bogen binnen de driehoek. Deze bogen moeten elkaar kruisen vanaf het punt waar ze de zijkanten raken.

Stap 4: Trek een lijn vanaf het hoekpunt van de driehoek tot waar de twee binnenste bogen elkaar kruisen.

kat timpf hoogte

Stap 5: Herhaal dezelfde stappen vanaf het andere hoekpunt van de driehoek.

Stap 6: Waar de twee lijnen elkaar ontmoeten of kruisen, bevindt zich het middelpunt van de driehoek.

In het midden van de rechthoekige driehoek

Het incenter als a Rechthoekige driehoek is het punt waar alle deellijnen van een rechthoekige driehoek samenkomen. Als de zijden van een rechthoekige driehoek a, b en c meten, wordt de straal van de cirkel ‘r’ gegeven als r = (ab)/(a + b + c). Het middelpunt van de rechthoekige driehoek wordt hieronder geïllustreerd:

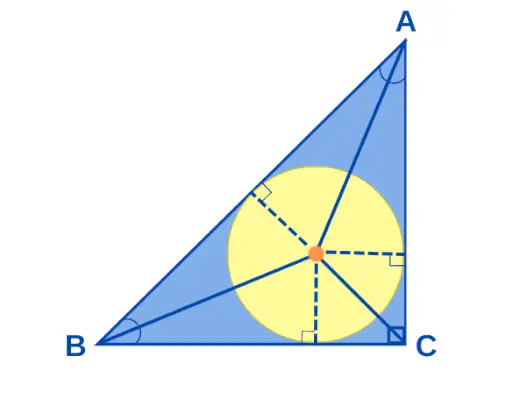
In het midden van een rechthoekige driehoek

Centroid, Circumcenter, Incenter, Orthocenter

Centroid, Circumcenter, Incenter en Orthocenter zijn de vier belangrijke punten die verband houden met een driehoek. Een vergelijking tussen Centroid, Circumcenter, Incenter en Orthocenter wordt hieronder weergegeven:

Controleer ook

• Gebied van Driehoek
• Omtrek van de driehoek
• Hoeksomeigenschap van een driehoek

Voorbeelden van het midden van een driehoek

Voorbeeld 1: Bereken het middelpunt van driehoek ABC. AB= 8 cm, BC= 15 cm, CA= 17 cm.

Oplossing:

Met behulp van de formule van Incenter van Driehoek = (aA + bB + cC)/(a + b + c)

waar,

• een = 8
• b = 15
• c = 17

En hoeken zijn,

• A = 30°
• B = 60°
• C = 90°

Door deze waarde in de te verkrijgen formule te plaatsen,

⇒ {(8)(30) + (15)(60) + (17)(90)}/{8 + 15 + 17}

⇒ (240 + 900 + 1530)/40

⇒ 2670/40

⇒ 66,75

Voorbeeld 2: Jane berekende de oppervlakte van een driehoekig veld als 120 vierkante meter. De omtrek van het veld is 36 meter. Als een cirkel zo in de driehoek wordt getekend dat deze elke zijde van de driehoek raakt, help Jane dan de inradius van de driehoek te berekenen.

Oplossing:

Volgens de gegeven informatie,

Oppervlakte van de driehoek = 120 vierkante meter

rij en kolom

Omtrek van de driehoek = 36 meter

We weten dat de oppervlakte van een driehoek = r × s

s = halve omtrek

s = p/2 = 36/2 = 18

EEN = r × s

r = A/s

r = 120/18

r = 6,67 meter

Oefenproblemen op het middelpunt van een driehoek

Probleem 1: Gegeven driehoek PQR met hoekpunten P(1, 2), Q(4, 6) en R(7, 2), zoek de coördinaten van het middenpunt.

Opgave 2: Construeer een driehoek ABC met ∠A = 45°, ∠B = 60° en ∠C = 75°. Gebruik de constructiemethode om het incenter te vinden.

Probleem 3: Als in driehoek LMN ∠L = 75°, ∠M = 60° en ∠N = 45°, zoek dan de coördinaten van het incenter.

Opgave 4: Construeer een driehoek XYZ met ∠X = 80°, ∠Y = 50° en ∠Z = 50°. Gebruik de constructiemethode om het incenter te vinden.

In het midden van een driehoek: veelgestelde vragen

Wat is het middelpunt van een driehoek?

Het middelpunt van een driehoek is het punt waar de deellijnen van de binnenhoeken elkaar snijden. Het ligt op gelijke afstand van alle drie de zijden van de driehoek.

converteer tekenreeks naar geheel getal

Wat is de betekenis van het Incenter in een driehoek?

Het incenter is belangrijk omdat dit het middelpunt is van de cirkel van de driehoek, de grootste cirkel die binnen de driehoek past. Het heeft de eigenschap dat het van alle kanten op gelijke afstand ligt.

Kan Incenter zich buiten de driehoek bevinden?

Nee, het middelpunt bevindt zich altijd binnen de driehoek. Het is het punt van gelijktijdigheid voor de bissectrices van de hoek, en moet per definitie binnen de grenzen van de driehoek liggen.

Hoe wordt Incenter gebouwd met behulp van een kompas en een richtliniaal?

Om het incenter te construeren, gebruikt u een kompas om bissectrices van elk hoekpunt naar de andere kant te tekenen. Het incenter is het punt waar deze bissectrices elkaar kruisen.

Wat is de Incenter-formule?

De formule voor het middelpunt van een driehoek kan als volgt worden geschreven:

frac{(aA+bB+cC)}{a+b+c}

Wat zijn eigenschappen van het middelpunt van een driehoek?

Het incenter heeft enkele belangrijke eigenschappen. Het ligt op gelijke afstand van de zijden van de driehoek, wat betekent dat de afstanden tot de zijden gelijk zijn. Het is ook het snijpunt van deellijnen van de hoek, waardoor de hoeken in twee gelijke delen worden verdeeld.

Hoe wordt Incentre bepaald?

Om het incenter te bepalen, moet u bepalen waar de bissectrices elkaar snijden. Dit kan gedaan worden met behulp van de incenterformule of door de bissectrices van de hoek te tekenen en hun snijpunt te vinden.

Wat is het verschil tussen Incentre en Circumcentre?

Het belangrijkste verschil tussen het incenter en het circumcenter is hun focus. De incenter houdt zich bezig met middelloodlijnen en is het middelpunt van de ingeschreven cirkel, terwijl de circumcenter zich bezighoudt met middelloodlijnen en het middelpunt is van de omgeschreven cirkel.

Zijn Incentre en Centroid hetzelfde?

Nee, het incenter en het zwaartepunt zijn verschillend. Het incenter is waar de bissectrices van de hoek samenkomen, terwijl het zwaartepunt is waar de medianen elkaar kruisen. Medianen verbinden hoekpunten met het middelpunt van de tegenoverliggende zijde.

Zijn Incentre en Orthocentrum hetzelfde?

Nee, het incenter en orthocenter zijn niet hetzelfde. Het incenter is het punt waar de hoeken elkaar doorsnijden, terwijl het orthocenter hoogten omvat: lijnen van elk hoekpunt loodrecht op de tegenoverliggende zijde. Het zijn verschillende punten in een driehoek.