Het Ford-Fulkerson-algoritme is een veelgebruikt algoritme om het maximale stromingsprobleem in een stromingsnetwerk op te lossen. Het maximale stromingsprobleem omvat het bepalen van de maximale hoeveelheid stroming die kan worden verzonden van een bronknooppunt naar een zinkpunt in een gerichte gewogen grafiek, afhankelijk van capaciteitsbeperkingen aan de randen.
Het algoritme werkt door iteratief een vergrotend pad te vinden, dat is een pad van de bron naar de put in de restgrafiek, dat wil zeggen de grafiek die wordt verkregen door de stroom af te trekken van de capaciteit van elke rand. Het algoritme verhoogt vervolgens de stroming langs dit pad met de maximaal mogelijke hoeveelheid, namelijk de minimale capaciteit van de randen langs het pad.
Probleem:
Gegeven een grafiek die een stroomnetwerk weergeeft waarbij elke rand een capaciteit heeft. Ook gegeven twee hoekpunten bron ‘s’ en wasbak ‘t’ in de grafiek, zoek de maximaal mogelijke stroom van s naar t met de volgende beperkingen:
- De stroom op een rand overschrijdt de gegeven capaciteit van de rand niet.
- De inkomende stroom is gelijk aan de uitgaande stroom voor elk hoekpunt behalve s en t.
Beschouw bijvoorbeeld de volgende grafiek uit het CLRS-boek.
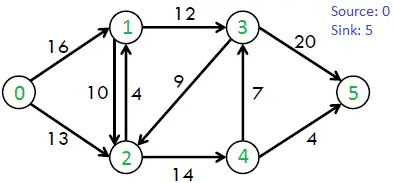
Het maximaal mogelijke debiet in de bovenstaande grafiek is 23.

Voorwaarde : Introductie van probleem met maximale stroom
Ford-Fulkerson-algoritme
Het volgende is een eenvoudig idee van het Ford-Fulkerson-algoritme:
- Begin met initiële stroom als 0.
- Hoewel er een groter pad bestaat van de bron naar de gootsteen:
- Vind een vergrotend pad met behulp van een padzoekalgoritme, zoals zoeken in de breedte of eerst in de diepte.
- Bepaal de hoeveelheid stroom die langs het vergrotende pad kan worden gestuurd, wat de minimale restcapaciteit langs de randen van het pad is.
- Verhoog de stroom langs het augmentatiepad met de bepaalde hoeveelheid.
- Retourneer de maximale stroom.
Tijdcomplexiteit: De tijdscomplexiteit van het bovenstaande algoritme is O(max_flow * E). We lopen een lus terwijl er een vergrotend pad is. In het ergste geval kunnen we in elke iteratie 1 eenheidsstroom toevoegen. Daarom wordt de tijdscomplexiteit O(max_flow * E).
arraylist in Java-sortering
Hoe implementeer je het bovenstaande eenvoudige algoritme?
Laten we eerst het concept van Residual Graph definiëren dat nodig is om de implementatie te begrijpen.
Residuele grafiek van een stroomnetwerk is een grafiek die extra mogelijke stroom aangeeft. Als er een pad is van bron naar put in de restgrafiek, dan is het mogelijk om stroom toe te voegen. Elke rand van een restgrafiek heeft een zogenaamde waarde restcapaciteit wat gelijk is aan de oorspronkelijke capaciteit van de rand minus de stroomsterkte. De resterende capaciteit is in feite de huidige capaciteit van de rand.
Laten we het nu hebben over de implementatiedetails. De restcapaciteit is 0 als er geen rand is tussen twee hoekpunten van de restgrafiek. We kunnen de restgrafiek initialiseren als de originele grafiek, omdat er geen initiële stroom is en de resterende capaciteit aanvankelijk gelijk is aan de oorspronkelijke capaciteit. Om een vergrotend pad te vinden, kunnen we een BFS of DFS van de restgrafiek uitvoeren. We hebben BFS gebruikt in de onderstaande implementatie. Met behulp van BFS kunnen we achterhalen of er een pad is van source naar sink. BFS bouwt ook een parent[]-array. Met behulp van de parent[]-array doorkruisen we het gevonden pad en vinden we een mogelijke stroom door dit pad door de minimale restcapaciteit langs het pad te vinden. Later voegen we de gevonden padstroom toe aan de algehele stroom.
Het belangrijkste is dat we de restcapaciteiten in de restgrafiek moeten bijwerken. We trekken de padstroom af van alle randen langs het pad en we voegen de padstroom langs de omgekeerde randen toe. We moeten de padstroom langs de omgekeerde randen toevoegen, omdat het later mogelijk nodig is om de stroom in omgekeerde richting te sturen (zie bijvoorbeeld de volgende link).
Hieronder vindt u de implementatie van het Ford-Fulkerson-algoritme. Om het simpel te houden, wordt de grafiek weergegeven als een 2D-matrix.
C++
// C++ program for implementation of Ford Fulkerson> // algorithm> #include> #include> #include> #include> using> namespace> std;> // Number of vertices in given graph> #define V 6> /* Returns true if there is a path from source 's' to sink> >'t' in residual graph. Also fills parent[] to store the> >path */> bool> bfs(>int> rGraph[V][V],>int> s,>int> t,>int> parent[])> {> >// Create a visited array and mark all vertices as not> >// visited> >bool> visited[V];> >memset>(visited, 0,>sizeof>(visited));> >// Create a queue, enqueue source vertex and mark source> >// vertex as visited> >queue<>int>>q;> >q.push(s);> >visited[s] =>true>;> >parent[s] = -1;> >// Standard BFS Loop> >while> (!q.empty()) {> >int> u = q.front();> >q.pop();> >for> (>int> v = 0; v if (visited[v] == false && rGraph[u][v]>0) {// Als we een verbinding met het sink-knooppunt vinden, // dan heeft BFS geen zin meer. We // hoeven alleen de ouder in te stellen en kunnen // true if (v == t) { parent[ v] = u; retourneer waar; } q.push(v); ouder[v] = u; bezocht[v] = waar; } } } // We hebben de sink in BFS niet bereikt vanaf de bron, dus // return false return false; } // Geeft de maximale stroom terug van s naar t in de gegeven grafiek int fordFulkerson(int graph[V][V], int s, int t) { int u, v; // Maak een restgrafiek en vul de restgrafiek // met gegeven capaciteiten in de originele grafiek als // restcapaciteiten in de restgrafiek int rGraph[V] [V]; // Residuele grafiek waarbij rGraph[i][j] // de resterende capaciteit van de rand aangeeft // van i tot j (als er een rand is. Als // rGraph[i][j] 0 is, dan is die er niet) for (u = 0; u for (v = 0; v rGraph[u][v] = graph[u][v]; int parent[V]; // Deze array wordt gevuld door BFS en // winkelpad int max_flow = 0; // Er is aanvankelijk geen stroom // Vergroot de stroom terwijl er een pad is van bron naar // sink while (bfs(rGraph, s, t, parent)) {// Vind de minimale restcapaciteit van de randen langs // het pad gevuld door BFS. Of we kunnen zeggen: zoek de // maximale stroom door het gevonden pad parent[v]; path_flow = min(path_flow, rGraph[u][v] } // update de resterende capaciteiten van de randen en // keer randen langs het pad om voor (v = t; v != s; v = parent[v]) { u = parent[v]; rGraph[u][v] -= path_flow; rGraph[v][u] += path_flow } // Padstroom toevoegen aan algemene stroom max_flow += path_flow; // Retourneer de algehele stroomretour max_flow; } // Stuurprogramma om bovenstaande functies te testen int main() {// Laten we een grafiek maken die wordt weergegeven in het bovenstaande voorbeeld int graph[V][V] = { { 0, 16, 13, 0, 0, 0 }, { 0, 0, 10, 12, 0, 0 }, { 0, 4, 0, 0, 14, 0 }, { 0, 0, 9, 0, 0, 20 }, { 0, 0, 0, 7 , 0, 4 }, { 0, 0, 0, 0, 0, 0 } }; uit<< 'The maximum possible flow is ' << fordFulkerson(graph, 0, 5); return 0; }> |
>
>
Java
// Java program for implementation of Ford Fulkerson> // algorithm> import> java.io.*;> import> java.lang.*;> import> java.util.*;> import> java.util.LinkedList;> class> MaxFlow {> >static> final> int> V =>6>;>// Number of vertices in graph> >/* Returns true if there is a path from source 's' to> >sink 't' in residual graph. Also fills parent[] to> >store the path */> >boolean> bfs(>int> rGraph[][],>int> s,>int> t,>int> parent[])> >{> >// Create a visited array and mark all vertices as> >// not visited> >boolean> visited[] =>new> boolean>[V];> >for> (>int> i =>0>; i visited[i] = false; // Create a queue, enqueue source vertex and mark // source vertex as visited LinkedList queue = new LinkedList(); queue.add(s); visited[s] = true; parent[s] = -1; // Standard BFS Loop while (queue.size() != 0) { int u = queue.poll(); for (int v = 0; v if (visited[v] == false && rGraph[u][v]>0) {/ // Als we een verbinding vinden met de sink // node, dan heeft BFS geen zin meer // We hoeven alleen maar de ouder in te stellen // en kunnen true retourneren if (v == t) { parent[ v] = u; retourneer waar; } wachtrij.add(v); ouder[v] = u; bezocht[v] = waar; } } } // We hebben de sink in BFS niet bereikt vanaf de bron, // dus return false return false; } // Geeft de maximale stroom terug van s naar t in de gegeven // graph int fordFulkerson(int graph[][], int s, int t) { int u, v; // Maak een restgrafiek en vul de rest // grafiek met gegeven capaciteiten in de originele grafiek // als restcapaciteiten in de restgrafiek // Residuele grafiek waarbij rGraph[i][j] aangeeft // restcapaciteit van rand van i tot j (als er // een rand is. Als rGraph[i][j] 0 is, dan is er // niet) int rGraph[][] = new int[V][V]; for (u = 0; u for (v = 0; v rGraph[u][v] = graph[u][v]; // Deze array wordt gevuld door BFS en om pad op te slaan int parent[] = new int[ V]; int max_flow = 0; // Er is aanvankelijk geen stroom // Vergroot de stroom terwijl er een pad is van de bron // naar sink while (bfs(rGraph, s, t, parent)) {// Zoek de minimale restcapaciteit van de randen // langs het pad gevuld door BFS. Of we kunnen zeggen // vind de maximale stroom door het gevonden pad ]) { u = parent[v]; path_flow = Math.min(path_flow, rGraph[u][v] } // update de restcapaciteiten van de randen en // keer randen langs het pad om voor (v = t; v != s; v = ouder[v]) { u = ouder[v]; rGraph[u][v] -= path_flow; flow max_flow += path_flow; } // Retourneer de algehele flow return max_flow; } // Stuurprogramma om bovenstaande functies te testen public static void main(String[] args) gooit java.lang.Exception {// Laten we een weergegeven grafiek maken in het bovenstaande voorbeeld int grafiek[][] = nieuwe int[][] { { 0, 16, 13, 0, 0, 0 }, { 0, 0, 10, 12, 0, 0 }, { 0, 4 , 0, 0, 14, 0 }, { 0, 0, 9, 0, 0, 20 }, { 0, 0, 0, 7, 0, 4 }, { 0, 0, 0, 0, 0, 0 } }; MaxFlow m = nieuwe MaxFlow(); System.out.println('De maximaal mogelijke stroom is ' + m.fordFulkerson(grafiek, 0, 5)); } }> |
>
salman khan khan leeftijd
>
Python
# Python program for implementation> # of Ford Fulkerson algorithm> from> collections>import> defaultdict> # This class represents a directed graph> # using adjacency matrix representation> class> Graph:> >def> __init__(>self>, graph):> >self>.graph>=> graph># residual graph> >self>. ROW>=> len>(graph)> ># self.COL = len(gr[0])> >'''Returns true if there is a path from source 's' to sink 't' in> >residual graph. Also fills parent[] to store the path '''> >def> BFS(>self>, s, t, parent):> ># Mark all the vertices as not visited> >visited>=> [>False>]>*>(>self>.ROW)> ># Create a queue for BFS> >queue>=> []> ># Mark the source node as visited and enqueue it> >queue.append(s)> >visited[s]>=> True> ># Standard BFS Loop> >while> queue:> ># Dequeue a vertex from queue and print it> >u>=> queue.pop(>0>)> ># Get all adjacent vertices of the dequeued vertex u> ># If a adjacent has not been visited, then mark it> ># visited and enqueue it> >for> ind, val>in> enumerate>(>self>.graph[u]):> >if> visited[ind]>=>=> False> and> val>>0>:> ># If we find a connection to the sink node,> ># then there is no point in BFS anymore> ># We just have to set its parent and can return true> >queue.append(ind)> >visited[ind]>=> True> >parent[ind]>=> u> >if> ind>=>=> t:> >return> True> ># We didn't reach sink in BFS starting> ># from source, so return false> >return> False> > > ># Returns the maximum flow from s to t in the given graph> >def> FordFulkerson(>self>, source, sink):> ># This array is filled by BFS and to store path> >parent>=> [>->1>]>*>(>self>.ROW)> >max_flow>=> 0> # There is no flow initially> ># Augment the flow while there is path from source to sink> >while> self>.BFS(source, sink, parent) :> ># Find minimum residual capacity of the edges along the> ># path filled by BFS. Or we can say find the maximum flow> ># through the path found.> >path_flow>=> float>(>'Inf'>)> >s>=> sink> >while>(s !>=> source):> >path_flow>=> min> (path_flow,>self>.graph[parent[s]][s])> >s>=> parent[s]> ># Add path flow to overall flow> >max_flow>+>=> path_flow> ># update residual capacities of the edges and reverse edges> ># along the path> >v>=> sink> >while>(v !>=> source):> >u>=> parent[v]> >self>.graph[u][v]>->=> path_flow> >self>.graph[v][u]>+>=> path_flow> >v>=> parent[v]> >return> max_flow> > # Create a graph given in the above diagram> graph>=> [[>0>,>16>,>13>,>0>,>0>,>0>],> >[>0>,>0>,>10>,>12>,>0>,>0>],> >[>0>,>4>,>0>,>0>,>14>,>0>],> >[>0>,>0>,>9>,>0>,>0>,>20>],> >[>0>,>0>,>0>,>7>,>0>,>4>],> >[>0>,>0>,>0>,>0>,>0>,>0>]]> g>=> Graph(graph)> source>=> 0>; sink>=> 5> > print> (>'The maximum possible flow is %d '> %> g.FordFulkerson(source, sink))> # This code is contributed by Neelam Yadav> |
>
>
C#
webbrowserinstellingen
// C# program for implementation> // of Ford Fulkerson algorithm> using> System;> using> System.Collections.Generic;> public> class> MaxFlow {> >static> readonly> int> V = 6;>// Number of vertices in> >// graph> >/* Returns true if there is a path> >from source 's' to sink 't' in residual> >graph. Also fills parent[] to store the> >path */> >bool> bfs(>int>[, ] rGraph,>int> s,>int> t,>int>[] parent)> >{> >// Create a visited array and mark> >// all vertices as not visited> >bool>[] visited =>new> bool>[V];> >for> (>int> i = 0; i visited[i] = false; // Create a queue, enqueue source vertex and mark // source vertex as visited List |
>
>
Javascript
> // Javascript program for implementation of Ford> // Fulkerson algorithm> // Number of vertices in graph> let V = 6;> // Returns true if there is a path from source> // 's' to sink 't' in residual graph. Also> // fills parent[] to store the path> function> bfs(rGraph, s, t, parent)> {> > >// Create a visited array and mark all> >// vertices as not visited> >let visited =>new> Array(V);> >for>(let i = 0; i visited[i] = false; // Create a queue, enqueue source vertex // and mark source vertex as visited let queue = []; queue.push(s); visited[s] = true; parent[s] = -1; // Standard BFS Loop while (queue.length != 0) { let u = queue.shift(); for(let v = 0; v { if (visited[v] == false && rGraph[u][v]>0) {/ // Als we een verbinding vinden met de sink // node, dan heeft BFS geen zin meer // We hoeven alleen maar de ouder in te stellen // en kunnen true retourneren if (v == t) { parent[ v] = u; retourneer waar; } wachtrij.push(v); ouder[v] = u; bezocht[v] = waar; } } } // We hebben de sink in BFS niet bereikt vanaf // vanaf de bron, dus return false return false; } // Geeft de maximale stroom terug van s naar t in // de gegeven grafiekfunctie fordFulkerson(graph, s, t) { let u, v; // Maak een restgrafiek en vul de // restgrafiek met gegeven capaciteiten // in de originele grafiek als rest // capaciteiten in restgrafiek // Residuele grafiek waarbij rGraph[i][j] // de restcapaciteit van de rand aangeeft / / van i tot j (als er een rand is. // Als rGraph[i][j] 0 is, dan is er // niet) let rGraph = new Array(V); for(u = 0; u { rGraph[u] = new Array(V); for(v = 0; v rGraph[u][v] = graph[u][v]; } // Deze array wordt gevuld door BFS en om pad op te slaan let parent = new Array(V); Er is aanvankelijk geen stroom let max_flow = 0; // Vergroot de stroom terwijl er // een pad is van bron naar sink while (bfs(rGraph, s, t) , parent)) {// Zoek de minimale restcapaciteit van de randen // langs het pad gevuld door BFS. Of we kunnen zeggen // vind de maximale stroom door het gevonden pad ; v != s; v = ouder[v]) { u = ouder[v]; path_flow = Math.min(path_flow, rGraph[u][v]); omgekeerde randen langs het pad for(v = t; v != s; v = parent[v]) { u = parent[v]; rGraph[u][v] -= rGraph[v][u] + = path_flow; } // Voeg padstroom toe aan de algehele stroom max_flow += path_flow; // Retourneer de algehele stroomretour max_flow } // Stuurprogrammacode // Laten we een grafiek maken die wordt weergegeven in het bovenstaande voorbeeld, let graph = [ [ 0 , 16, 13, 0, 0, 0 ], [ 0, 0, 10, 12, 0, 0 ], [ 0, 4, 0, 0, 14, 0 ], [ 0, 0, 9, 0, 0 , 20], [0, 0, 0, 7, 0, 4], [0, 0, 0, 0, 0, 0]]; document.write('De maximaal mogelijke stroom is ' + fordFulkerson(grafiek, 0, 5)); // Deze code is bijgedragen door avanitrachhadiya2155> |
>
>Uitvoer
The maximum possible flow is 23>
Tijdcomplexiteit: O(|V| * E^2) , waarbij E het aantal randen is en V het aantal hoekpunten.
Ruimtecomplexiteit: O(V), terwijl we een wachtrij creëerden.
De bovenstaande implementatie van het Ford Fulkerson-algoritme wordt genoemd Edmonds-Karp-algoritme . Het idee van Edmonds-Karp is om BFS te gebruiken in de Ford Fulkerson-implementatie, aangezien BFS altijd een pad kiest met een minimaal aantal randen. Wanneer BFS wordt gebruikt, kan de tijdscomplexiteit in het slechtste geval worden teruggebracht tot O(VE2). De bovenstaande implementatie maakt echter gebruik van de representatie van de aangrenzende matrix, waarbij BFS O(V2) tijd, is de tijdscomplexiteit van de bovenstaande implementatie O(EV3) (Refereren CLRS-boek voor bewijs van tijdscomplexiteit)
Dit is een belangrijk probleem, aangezien het zich in veel praktijksituaties voordoet. Voorbeelden zijn onder meer het maximaliseren van het transport met gegeven verkeerslimieten, het maximaliseren van de pakketstroom in computernetwerken.
Dinc's algoritme voor Max-Flow.
Oefening:
Wijzig de bovenstaande implementatie zodat deze in O(VE2) tijd.
