1. DFA: DFA verwijst naar deterministische eindige automaat. Er wordt gezegd dat een eindige automaat (FA) deterministisch is als hij overeenkomt met een invoersymbool en er één enkele resulterende toestand is, dat wil zeggen dat er slechts één overgang is. Een deterministische eindige automaten is een set van vijf tupels, weergegeven als:
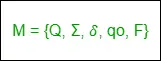
Waar,
Vraag: Een niet-lege eindige reeks toestanden in de eindige controle (qo, q1, q2, ...).
Σ: Een niet-lege eindige set invoersymbolen.
δ: Het is een overgangsfunctie die twee argumenten nodig heeft, een toestand en een invoersymbool, en retourneert een enkele toestand.
qo: Het is de startstatus, een van de staten in Q.
F: Het is een niet-lege verzameling eindtoestanden/accepterende toestanden uit de verzameling die bij Q hoort.
2. OORZAKEN:
NFA verwijst naar niet-deterministische eindige automaat. Er wordt gezegd dat een eindige automaat (FA) niet-deterministisch is als er meer dan één mogelijke overgang van één toestand op hetzelfde invoersymbool is.
Een niet-deterministische eindige automaten zijn ook een set van vijf tupels en weergegeven als:
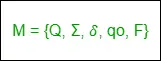
Waar,
Vraag: Een reeks niet-lege eindige toestanden.
Σ: Een reeks niet-lege eindige invoersymbolen.
δ: Het is een overgangsfunctie die een toestand van Q en een invoersymbool van Q overneemt en een deelverzameling van Q retourneert.
qo: Beginstatus van NFA en lid van Q.
F: Een niet-lege reeks eindtoestanden en lid van Q.
Voorwaarde - Afgewerkt automatisch
Verschil tussen DFA en NFA:
| DFA | NFA |
|---|---|
| DFA staat voor Deterministische Eindige Automaten. | NFA staat voor Niet-deterministische Eindige Automaten. |
| Voor elke symbolische representatie van het alfabet is er slechts één toestandsovergang in DFA. | Het is niet nodig om te specificeren hoe de NFA reageert volgens een bepaald symbool. |
| DFA kan de lege tekenreeksovergang niet gebruiken. | NFA kan een lege tekenreeksovergang gebruiken. |
| DFA kan worden opgevat als één machine. | NFA kan worden opgevat als meerdere kleine machines die tegelijkertijd aan het werk zijn. |
| In DFA wordt de volgende mogelijke toestand duidelijk ingesteld. | In NFA kan elk paar toestanden en invoersymbolen vele mogelijke volgende toestanden hebben. |
| DFA is moeilijker te construeren. | NFA is gemakkelijker te construeren. |
| DFA wijst de tekenreeks af als deze eindigt in een staat die afwijkt van de accepterende staat. | NFA wijst de string af als alle vestigingen doodgaan of de string weigeren. |
| De tijd die nodig is voor het uitvoeren van een invoerreeks is minder. | De tijd die nodig is voor het uitvoeren van een invoerreeks is langer. |
| Alle DFA zijn NFA. | Niet alle NFA zijn DFA. |
| DFA vereist meer ruimte. | NFA heeft minder ruimte nodig dan DFA. |
| Dode configuratie is niet toegestaan. bijv.: als we invoer als 0 geven op de status q0, moeten we 1 opgeven als invoer voor q0 als zelflus. | Dode configuratie is toegestaan. bijv.: als we invoer als 0 geven voor de status q0, kunnen we de volgende invoer 1 geven voor q1, die naar de volgende status gaat. |
| δ: QxΣ -> Q, d.w.z. de volgende mogelijke toestand behoort tot Q. | δ: Qx(Σ U ε) -> 2^Q, d.w.z. de volgende mogelijke toestand behoort tot de machtsverzameling van Q. |
| Backtracking is toegestaan in DFA. | Backtracking is niet altijd mogelijk in NFA. |
| Conversie van reguliere expressie naar DFA is moeilijk. | Conversie van reguliere expressie naar NFA is eenvoudiger vergeleken met DFA. |
| Epsilon-verplaatsing is niet toegestaan in DFA | Epsilon-beweging is toegestaan in NFA |
| DFA staat slechts één zet toe voor een alfabet met één invoer. | Er kan keuze zijn (meer dan één zet) voor een alfabet met één invoer. |
