Finite Automata(FA) is de eenvoudigste machine om patronen te herkennen. Het wordt gebruikt om een reguliere taal te karakteriseren, bijvoorbeeld: /baa+!/.
Het wordt ook gebruikt om natuurlijke taaluitdrukkingen te analyseren en te herkennen. De eindige automaten of eindige toestandsmachine is een abstracte machine die vijf elementen of tupels heeft. Het heeft een reeks toestanden en regels om van de ene toestand naar de andere te gaan, maar dit hangt af van het toegepaste invoersymbool. Op basis van de statussen en de set regels kan de invoerreeks worden geaccepteerd of afgewezen. Kortom, het is een abstract model van een digitale computer die een invoerreeks leest en de interne status ervan verandert afhankelijk van het huidige invoersymbool. Elke automaat definieert een taal, dat wil zeggen een reeks tekenreeksen die hij accepteert. De volgende afbeelding toont enkele essentiële kenmerken van algemene automatisering.
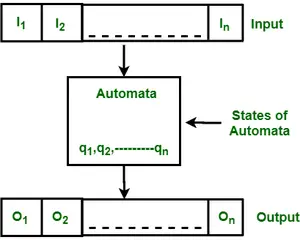
Figuur: Kenmerken van eindige automaten
De bovenstaande afbeelding toont de volgende kenmerken van automaten:
- Invoer
- Uitvoer
- Staten van automaten
- Staatsrelatie
- Uitgangsrelatie
Een eindige automaat bestaat uit het volgende:
Q : Finite set of states. ? : set of Input Symbols. q : Initial state. F : set of Final States. ? : Transition Function.>
Formele specificatie van de machine is
{ Q, ?, q, F, ? }> FA wordt gekarakteriseerd in twee typen:
1) Deterministische eindige automaten (DFA):
DFA consists of 5 tuples {Q, ?, q, F, ?}. Q : set of all states. ? : set of input symbols. ( Symbols which machine takes as input ) q : Initial state. ( Starting state of a machine ) F : set of final state. ? : Transition Function, defined as ? : Q X ? -->V.> In een DFA gaat de machine voor een bepaald invoerteken slechts naar één status. Voor elk invoersymbool wordt voor elke toestand een overgangsfunctie gedefinieerd. Ook in DFA is null (of ?) verplaatsing niet toegestaan, dat wil zeggen dat DFA de status niet kan veranderen zonder enig invoerteken.
Construeer bijvoorbeeld een DFA die een taal accepteert waarvan alle strings eindigen op ‘a’.
Gegeven: ? = {a,b}, q = {q0}, F={q1}, Q = {q0, Q1}
azuur abonnement
Overweeg eerst een taalset van alle mogelijke acceptabele strings om een nauwkeurig statusovergangsdiagram te construeren.
L = {a, aa, aaa, aaaa, aaaaa, ba, bba, bbba, vader, vader, vader, vader}
Hierboven ziet u een eenvoudige subset van de mogelijke acceptabele strings. Er kunnen nog veel andere strings zijn die eindigen op 'a' en symbolen {a,b} bevatten.
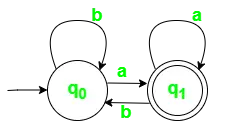
Fig. 1. Statusovergangsdiagram voor DFA met ? = {een, b}
Snaren die niet worden geaccepteerd zijn,
ab, bb, aab, abb, enz.
Toestandsovergangstabel voor bovenstaande automaat,
| ?StaatSymbool? | A | B |
|---|---|---|
| Q0 | Q1 | Q0 |
| Q1 | Q1 | Q0 |
Een belangrijk ding om op te merken is, er kunnen veel mogelijke DFA's voor een patroon zijn . Een DFA met een minimum aantal staten heeft over het algemeen de voorkeur.
2) Niet-deterministische eindige automaten (NFA): NFA is vergelijkbaar met DFA, behalve de volgende extra functies:
- Een nul- (of ?) zet is toegestaan, dat wil zeggen dat hij vooruit kan gaan zonder symbolen te lezen.
- Mogelijkheid om naar een willekeurig aantal staten te verzenden voor een bepaalde invoer.
Deze bovenstaande functies voegen echter geen kracht toe aan NFA. Als we beide vergelijken in termen van kracht, zijn beide gelijkwaardig.
Door bovenstaande extra features heeft NFA een andere transitiefunctie, de rest is hetzelfde als DFA.
?: Transition Function ?: Q X (? U ? ) -->2 ^ Vraag>
Zoals je kunt zien in de overgangsfunctie is voor elke invoer inclusief null (of ?), NFA naar elk staatsaantal toestanden te gaan. Hieronder vindt u bijvoorbeeld een NFA voor het bovenstaande probleem.
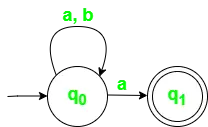
Fig. 2. Statusovergangsdiagram voor NFA met ? = {een, b}
Staatsovergangstabel voor bovenstaande automaat,
| ?StaatSymbool? | A | B |
|---|---|---|
| Q0 | {Q0,Q1} | Q0 |
| Q1 | ? | ? |
Een belangrijk ding om op te merken is, als in NFA een pad voor een invoerreeks naar een eindtoestand leidt, dan de invoerreeks is geaccepteerd . In de bovenstaande NFA zijn er bijvoorbeeld meerdere paden voor de invoerreeks 00. Omdat een van de paden naar een eindtoestand leidt, wordt 00 geaccepteerd door de bovenstaande NFA.
Enkele belangrijke punten:
- Rechtvaardiging:
In case of DFA ? : Q X ? -->V In geval van NFA? : Q X ? --> 2Q>
Als je nu observeert, zul je ontdekken dat Q X? –> Q is onderdeel van Q X ? –> 2Q.
Aan de RHS-kant is Q de deelverzameling van 2Qwat aangeeft dat Q in 2 zitQof Q is een deel van 2QHet omgekeerde is echter niet waar. Wiskundig gezien kunnen we dat dus concluderen elke DFA is NFA, maar niet andersom . Toch is er een manier om een NFA om te zetten naar DFA, dus er bestaat een gelijkwaardige DFA voor elke NFA .
- Zowel NFA als DFA hebben dezelfde kracht en elke NFA kan worden vertaald in een DFA.
- Er kunnen meerdere eindstatussen zijn in zowel DFA als NFA.
- NFA is meer een theoretisch concept.
- DFA wordt gebruikt bij lexicale analyse in Compiler.
- Als het aantal staten in de NFA N is, kan de DFA maximaal 2 hebbenNaantal staten.
Zie Quiz over reguliere expressie en eindige automaten.
