Vereiste – Datamining, gelijkenismeting verwijst naar afstand waarbij dimensies de kenmerken van het data-object in een dataset vertegenwoordigen. Als deze afstand kleiner is, zal er een hoge mate van gelijkenis zijn, maar als de afstand groot is, zal er een lage mate van gelijkenis zijn. Enkele van de populaire gelijkenismaatregelen zijn:
- Euclidische afstand.
- Manhattan-afstand.
- Jaccard-gelijkenis.
- Minkowski-afstand.
- Cosinus gelijkenis.
Cosinus gelijkenis is een metriek die helpt bij het bepalen hoe vergelijkbaar de gegevensobjecten zijn, ongeacht hun grootte. We kunnen de gelijkenis tussen twee zinnen in Python meten met behulp van Cosinus Gelijkenis. Bij cosinusgelijkenis worden dataobjecten in een dataset behandeld als een vector. De formule om de cosinusovereenkomst tussen twee vectoren te vinden is –
(x, y) = x . y / ||x|| ||y||>
waar,
- X . y = product (punt) van de vectoren ‘x’ en ‘y’.||x|| En ||en|| = lengte (grootte) van de twee vectoren ‘x’ en ‘y’.||x||
||en|| = regulier product van de twee vectoren ‘x’ en ‘y’. Voorbeeld : Beschouw een voorbeeld om de gelijkenis tussen twee vectoren te vinden: 'X' En 'En' , met behulp van cosinusgelijkenis. De ‘x’-vector heeft waarden, x = { 3, 2, 0, 5 } De ‘y’-vector heeft waarden, j = { 1, 0, 0, 0 } De formule voor het berekenen van de cosinusovereenkomst is: 
(x, y) = x. y / ||x|| ||en||
x . y = 3*1 + 2*0 + 0*0 + 5*0 = 3 ||x|| = √ (3)^2 + (2)^2 + (0)^2 + (5)^2 = 6.16 ||y|| = √ (1)^2 + (0)^2 + (0)^2 + (0)^2 = 1 ∴ (x, y) = 3 / (6.16 * 1) = 0.49>
Het verschil tussen de twee vectoren ‘x’ en ‘y’ wordt gegeven door –
∴ (x, y) = 1 - (x, y) = 1 - 0.49 = 0.51>
- De cosinusovereenkomst tussen twee vectoren wordt gemeten in ‘θ’.
- Als θ = 0° overlappen de vectoren ‘x’ en ‘y’, wat bewijst dat ze vergelijkbaar zijn.
- Als θ = 90° zijn de ‘x’- en ‘y’-vectoren verschillend.
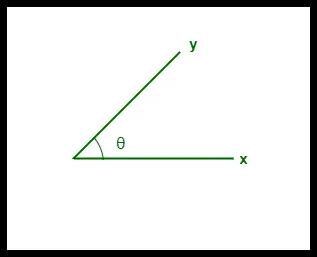
Cosinus Overeenkomst tussen twee vectoren
Voordelen:
- De cosinus-overeenkomst is gunstig omdat zelfs als de twee vergelijkbare gegevensobjecten vanwege de grootte ver uit elkaar liggen op de Euclidische afstand, ze nog steeds een kleinere hoek tussen hen kunnen hebben. Hoe kleiner de hoek, hoe groter de gelijkenis.
- Wanneer de cosinusovereenkomst in een multidimensionale ruimte wordt geplot, wordt de oriëntatie (de hoek) van de dataobjecten vastgelegd en niet de grootte.