Binair getalsysteem is een getalsysteem dat wordt gebruikt om verschillende getallen weer te geven met slechts twee symbolen 0 en 1. Het woord binair is afgeleid van het woord bi dat twee betekent. Daarom wordt dit nummersysteem het binaire nummersysteem genoemd. Het binaire getalsysteem is dus een systeem dat slechts twee symbolen heeft.
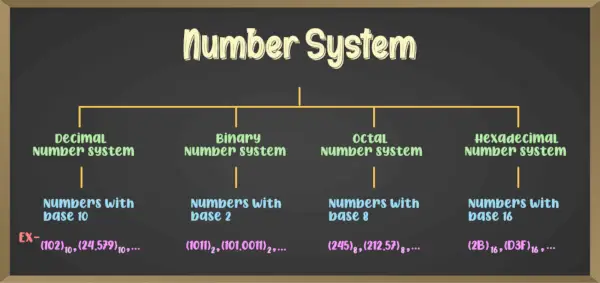
Er zijn over het algemeen verschillende soorten nummersystemen, waarvan de vier belangrijkste zijn:
- Binair getalsysteem (nummersysteem met grondtal 2)
- Octaal nummersysteem (nummersysteem met grondtal 8)
- Decimaal getalsysteem (nummersysteem met grondtal 10)
- Hexadecimaal getalsysteem (nummersysteem met grondtal 16)
Hier gaan we alleen leren over het binaire getalsysteem. Dit nummersysteem is erg handig voor het uitleggen van taken aan de computer. In het binaire getalsysteem hebben we twee toestanden 0 en 1 en deze twee toestanden worden weergegeven door twee toestanden van een transistor. Als de stroom door de transistor gaat, leest de computer 1 en als de stroom afwezig is door de transistor, leest hij 0. Dus door de stroom af te wisselen, leest de computer het binaire getalsysteem. Elk cijfer in het binaire getalsysteem wordt een bit genoemd.
In dit artikel zullen we in detail leren over het binaire getalsysteem, de conversie van het binaire getalsysteem, de binaire tabel, de werking van binaire getallen, voorbeelden en andere.
Inhoudsopgave
- Binair getalsysteem
- Binaire getallentabel
- Binair naar decimaal conversie
- Decimaal naar binair conversie
- Rekenkundige bewerkingen op binaire getallen
- 1's en 2's complement van een binair getal
- Gebruik van binair getalsysteem
- Voorbeeld van een binair getalsysteem
Binair getalsysteem
Binair nummersysteem is het nummersysteem waarin we twee cijfers 0 en 1 gebruiken om alle noodzakelijke bewerkingen uit te voeren. In het binaire getalsysteem hebben we een grondtal van 2. De basis van het binaire getallenstelsel wordt ook wel de radix van de nummer systeem .
In een binair getalsysteem vertegenwoordigen we het getal als:
- (11001)2
In het bovenstaande voorbeeld wordt een binair getal gegeven waarvan het grondtal 2 is. In een binair getalsysteem wordt elk cijfer de bit genoemd. In het bovenstaande voorbeeld zijn er 5 cijfers.
Binaire getallentabel
| Decimaal getal | Binair getal | Decimaal getal | Binair getal |
|---|---|---|---|
| 1 | 001 diff in python | elf | 1011 |
| 2 | 010 | 12 | 1100 |
| 3 | 011 | 13 | 1101 |
| 4 | 100 | 14 | 1110 |
| 5 | 101 | vijftien | 1111 |
| 6 | 110 | 16 | 10000 |
| 7 | 111 | 17 | 10001 |
| 8 | 1000 | 18 | 10010 |
| 9 | 1001 | 19 | 10011 |
| 10 | 1010 karakter in tekenreeks | twintig | 10100 |
Binair naar decimaal conversie
Een binair getal wordt omgezet in een decimaal getal door elk cijfer van het binaire getal te vermenigvuldigen met de macht van 1 of 0 tot de overeenkomstige macht van 2. Laten we bedenken dat een binair getal n cijfers heeft, B = an-1…A3A2A1A0. Nu wordt het overeenkomstige decimale getal gegeven als
D = (een n-1 ×2 n-1 ) +…+(een 3 ×2 3 ) + (een 2 ×2 2 ) + (een 1 ×2 1 ) + (een 0 ×2 0 )
Laten we een voorbeeld bekijken om het concept beter te begrijpen.
Voorbeeld: Converteren (10011) 2 naar een decimaal getal.
Oplossing:
Het gegeven binaire getal is (10011)2.
(10011)2= (1 × 24) + (0 × 23) + (0 × 22) + (1×21) + (1×20)
= 16 + 0 + 0 + 2 + 1 = (19)10
Daarom is het binaire getal (10011)2wordt uitgedrukt als (19)10.
Decimaal naar binair conversie
Een decimaal getal wordt omgezet in een binair getal door het gegeven decimale getal continu door 2 te delen totdat we het quotiënt als 1 krijgen, en we schrijven de getallen van beneden naar boven.
Laten we een voorbeeld bekijken om het concept beter te begrijpen.
Voorbeeld: Converteren (28) 10 in een binair getal.
Oplossing:
Daarom (28)10wordt uitgedrukt als (11100)2.
Rekenkundige bewerkingen op binaire getallen
We kunnen eenvoudig verschillende bewerkingen uitvoeren op binaire getallen. Verschillende rekenkundige bewerkingen op het binaire getal omvatten:
- Binaire optelling
- Binaire aftrekking
- Binaire vermenigvuldiging
- Binaire divisie
Laten we nu hetzelfde in detail leren kennen.
Binaire optelling
Het resultaat van de optelling van twee binaire getallen is ook een binair getal. Om het resultaat van de optelling van twee binaire getallen te verkrijgen, moeten we het cijfer van de binaire getallen per cijfer optellen. De onderstaande tabel toont de regel van binaire optelling.
| Binair getal (1) | Binair getal (2) | Toevoeging | Dragen |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 gebruik van besturingssysteem | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Binaire aftrekking
Het resultaat van het aftrekken van twee binaire getallen is ook een binair getal. Om het resultaat van het aftrekken van twee binaire getallen te verkrijgen, moeten we het cijfer van de binaire getallen per cijfer aftrekken. De onderstaande tabel toont de regel van binaire aftrekking.
| Binair getal (1) | Binair getal (2) | Aftrekken | Lenen |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
Binaire vermenigvuldiging
Het vermenigvuldigingsproces van binaire getallen is vergelijkbaar met de vermenigvuldiging van decimale getallen. De regels voor het vermenigvuldigen van twee binaire getallen worden gegeven in de tabel:
| Binair getal (1) | Binair getal (2) | Vermenigvuldiging |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 kenmerken van Java | 1 |
Binaire divisie
De manier van delen voor binaire getallen is vergelijkbaar met die van de decimale getaldelingsmethode. Laten we een voorbeeld bekijken om het concept beter te begrijpen.
Voorbeeld: delen (101101) 2 door (110) 2
Oplossing:
1's en 2's complement van een binair getal
- Het 1-complement van een binair getal wordt verkregen door de cijfers van het binaire getal om te keren.
Voorbeeld: Vind het 1-complement van (10011) 2 .
Oplossing:
Gegeven binair getal is (10011)2
Om het 1-complement te vinden, moeten we de cijfers van het gegeven getal omkeren.
Dus 1's complement van (10011)2is (01100)2
- Het 2-complement van een binair getal wordt verkregen door de cijfers van het binaire getal om te keren en vervolgens 1 toe te voegen aan het minst significante bit.
Voorbeeld: Vind het 2-complement van (1011) 2 .
Oplossing:
Gegeven binair getal is (1011)2
Om het complement van de 2 te vinden, moet je eerst het complement van de 1 vinden, d.w.z. (0100)2
Als we nu 1 optellen bij het minst significante bit, krijgen we (0101)2
Daarom is het 2-complement van (1011)2is (0101)2
Gebruik van binair getalsysteem
Binaire getalsystemen worden voor verschillende doeleinden gebruikt en het belangrijkste gebruik van het binaire getalsysteem is:
- Binair nummersysteem wordt in alle digitale elektronica gebruikt voor het uitvoeren van verschillende bewerkingen.
- Programmeertalen gebruiken een binair nummersysteem voor het coderen en decoderen van gegevens.
- Binair getalsysteem wordt in Data Sciences voor verschillende doeleinden gebruikt, enz.
Lees verder,
- Binaire formule
- Verschil tussen decimale en binaire getalsystemen
Voorbeeld van een binair getalsysteem
Voorbeeld 1: Decimaal getal converteren (98) 10 in binair.
Oplossing:
Dus binair getal voor (98)10is gelijk aan (1100010)2
Voorbeeld 2: Converteer binair getal (1010101) 2 naar decimaal getal.
Oplossing:
Gegeven binair getal, (1010101)2
= (1 × 20) + (0 × 21) + (1×22) + (0 × 23) + (1×24) + (0 × 25) + (1×26)
= 1 + 0 + 4 + 0 + 16 + 0 + 64
= (85)10
Dus binair getal (1010101)2is gelijk aan (85)10in decimaal systeem.
Voorbeeld 3: Delen (11110) 2 door (101) 2
Oplossing:
Voorbeeld 4: Optellen (11011) 2 en (10100) 2
soorten softwaretesten
Oplossing:
Daarom (11011)2+ (10100)2= (101111)2
Voorbeeld 5: Aftrekken (11010) 2 en (10110) 2
Oplossing:
Daarom (11010)2– (10110)2= (00100)2
Voorbeeld 6: Vermenigvuldigen (1110) 2 en (1001) 2 .
Oplossing:
Dus (1110)2× (1001)2= (1111110)2
Veelgestelde vragen over binair getalsysteem
Wat is een binair getalsysteem?
Binair getalsysteem is een van de vier getallensystemen die worden gebruikt om de getallen weer te geven met slechts twee cijfers, 0 en 1. In het binaire getalsysteem worden de cijfers 'bits' genoemd. Binair getalsysteem wordt door computers gebruikt om verschillende berekeningen uit te voeren.
Wat is een B Het?
Een bit in het binaire getalsysteem wordt gedefinieerd als individuele cijfers die de waarde ‘0’ of ‘1’ bevatten.
Wat is een knabbel?
Een groep van vier cijfers wordt de Niblle genoemd.
Wat is de binaire waarde van 10?
Binaire waarde van 10 is (1010)2
Wat zijn soorten nummersystemen?
Er zijn verschillende soorten nummersystemen en sommige daarvan zijn:
- Binair getalsysteem
- Octaal getalsysteem
- Decimaal getalsysteem
- Hexadecimaal getalsysteem
Hoe binaire getallen berekenen?
Binaire getallen worden berekend op basis van dimale getallen door het decimale getal door 2 te delen en de rest op te schrijven. Vervolgens rangschikken we alle resten van nieuw naar oud om het binaire getal te krijgen.
Hoe binaire getallen toevoegen?
Binaire getallen worden toegevoegd met behulp van de onderstaande formules:
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 0 (1 meenemen)






