Een binaire boom is in evenwicht als de hoogte van de boom O(Log n) is, waarbij n het aantal knooppunten is. De AVL-boom behoudt bijvoorbeeld de O(Log n)-hoogte door ervoor te zorgen dat het hoogteverschil tussen de linker- en rechtersubboom maximaal 1 is. Rood-zwarte bomen behouden de O(Log n)-hoogte door ervoor te zorgen dat het aantal van zwarte knooppunten op elk wortel-tot-blad-pad hetzelfde is en dat er geen aangrenzende rode knooppunten zijn. Gebalanceerde binaire zoekbomen zijn qua prestaties goed omdat ze O(log n) tijd bieden voor zoeken, invoegen en verwijderen.

Een gebalanceerde binaire boom is een binaire boom die aan de 3 voorwaarden voldoet:

• De hoogte van de linker- en rechterboom voor elk knooppunt verschilt niet meer dan 1.
• De linker subboom van dat knooppunt is ook in evenwicht.
• De rechter subboom van dat knooppunt is ook in evenwicht.

Eén enkel knooppunt is altijd in evenwicht. Het wordt ook wel een in hoogte gebalanceerde binaire boom genoemd.

Voorbeeld :

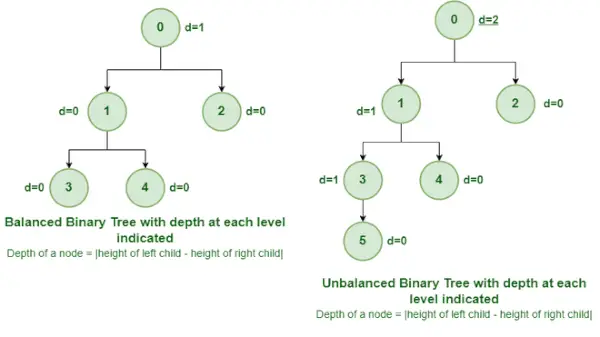
Evenwichtige en onevenwichtige binaire boom

Het is een soort binaire boom waarin het verschil tussen de hoogte van de linker en de rechter subboom voor elk knooppunt 0 of 1 is. In de bovenstaande afbeelding is het hoofdknooppunt met de waarde 0 uit balans met een diepte van 2 eenheden .

Toepassing van gebalanceerde binaire boom:

• AVL-bomen
• Rode Zwarte Boom
• Evenwichtige binaire zoekboom

Voordelen van gebalanceerde binaire boom:

• Niet-destructieve updates worden ondersteund door een gebalanceerde binaire boom met dezelfde asymptotische effectiviteit.
• Bereikquery's en iteratie in de juiste volgorde worden mogelijk gemaakt door de gebalanceerde binaire boom.