Wiskunde is een fascinerend onderwerp dat bestaat uit een breed scala aan concepten en principes; Eén zo'n concept is exponentiële notatie . Exponentiële notatie is een fundamenteel concept waarbij een grondtal wordt verhoogd tot een specifieke macht (of exponent). Dit is een krachtig concept dat wordt gebruikt om grote en minimale getallen op een geschiktere manier uit te drukken; een voorbeeld hiervan wordt in dit artikel besproken, namelijk 10 tot de 5^eStroom. In dit artikel zullen we dus het concept van exponentiële notatie leren kennen, de betekenis van de 10 tot de 5 bespreken^ePower, leer over verschillende manieren om deze waarde uit te drukken, en bespreek de toepassingen van exponentiële notatie op verschillende andere gebieden dan wiskunde.

Exponentiële notatie definiëren

Exponentiële of wetenschappelijke notatie biedt een gestandaardiseerde en georganiseerde methode voor het weergeven van getallen. Het is nuttig als we met grote en kleine aantallen te maken hebben, omdat het de uitdrukking ervan vereenvoudigt en de duidelijkheid vergroot.

Delen van wetenschappelijke notatie

Deze notatie bestaat uit twee delen:

1. Het basisnummer
2. Het exponent- (of machts-) getal

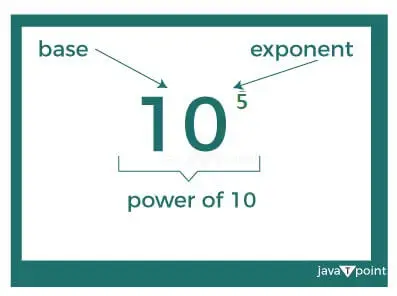
Het grondtal is 10 en de exponent is 5, wat aangeeft hoe vaak het grondtal (10) met zichzelf wordt vermenigvuldigd; Dit betekent dat 10 tot de Macht van 5 is gelijk aan 10, 5 keer met zichzelf vermenigvuldigd .

Impliceert 10 x 10 x 10 x 10 x 10 = 10⁵

10 tot de 5 uitdrukken^eStroom

Er zijn veel manieren om 10 tot de 5e macht uit te drukken of weer te geven, wat ook afhangt van het veld waarin het wordt gebruikt of van persoonlijke voorkeur.

Wetenschappelijke notatie:De meest eenvoudige weergave is 10⁵, waarbij 10 het grondtal is en 5 een exponent of macht is; dit formaat is meestal begrijpelijk en wordt vaak gebruikt in de wiskundige en wetenschappelijke literatuur.Numerieke weergave:Een andere manier om 10 uit te drukken in de Macht van 5 is door het getal in zijn uitgebreide vorm, 100.000, te schrijven. Dit formaat verdeelt het getal in cijfers en benadrukt de omvang ervan om de betekenis ervan te begrijpen.Lange vorm:De lange representatie van 10 tot de Macht van 5 is 'één lakh'. We gebruiken dit formaat in ons dagelijks taalgebruik, waardoor we het getal gemakkelijker kunnen begrijpen.

Significant

10 tot de 5^eMacht is op verschillende gebieden erg belangrijk geweest, vooral in wetenschappelijk onderzoek, technologie en het dagelijks leven; het vertegenwoordigt de waarde van één lakh, gelijk aan 1, gevolgd door vijf nullen, dat wil zeggen 100.000. In wetenschappelijke notaties wordt deze waarde vaak gebruikt wanneer we grote hoeveelheden meten, zoals de afstand tussen planeten en hemellichamen, het tellen van het aantal sterren in het universum en de wereldbevolking. Het helpt wetenschappers en onderzoekers deze zeer grote hoeveelheden gemakkelijker uit te drukken en maakt het voor hen gemakkelijker om die gegevens te begrijpen en te analyseren.

Toepassingen van 10 tot de 5^eStroom

Nu we de berekening begrijpen, gaan we enkele praktische toepassingen verkennen waarbij we de relevantie van de 10 tot de 5 kunnen vinden^eStroom:

Digitale technologie:In computers en digitale technologie spelen machten van 10 een belangrijke rol. Computers slaan informatie op en verwerken deze met behulp van binaire code op basis van een tweecijferig systeem (0 en 1). Machten van 2, nauw verwant aan machten van 10, worden gebruikt om de grootte van de geheugenkaart, de gegevensoverdrachtsnelheid en de snelheid van de processors weer te geven.Bevolkingsgroei:Exponentiële groei wordt vaak waargenomen bij natuurverschijnselen, waaronder bevolkingsgroei. Het concept van 10 tot de 5^eMacht kan ons helpen begrijpen hoe populaties in de loop van de tijd snel kunnen toenemen; Als een populatie van 100.000 individuen bijvoorbeeld met 10% per jaar groeit, zou deze na vier jaar ongeveer 14.6410 bereiken.Wetenschappelijke notatie:10 tot de 5^eMacht is een cruciaal onderdeel van wetenschappelijke notatie. Deze notatie drukt zeer grote of minimale getallen uit in een beter beheersbaar formaat.Schaal en omvang:Machten van 10 worden vaak gebruikt om de uitgestrektheid of kleinheid van objecten of verschijnselen te beschrijven. Astronomen gebruiken bijvoorbeeld het concept van een lichtjaar, de afstand die het licht in één jaar aflegt.Grote getallen berekenen:Op gebieden als financiën, natuurkunde en techniek zijn meestal grote numerieke berekeningen betrokken. Exponentiële notatie is waardevol bij het vereenvoudigen van deze berekeningen, omdat het een compacte weergave mogelijk maakt en de kans op fouten verkleint.

Conclusie

Het begrijpen van machtsverheffen is een essentiële vaardigheid voor het uitdrukken van getallen tot verschillende machten. In dit artikel hebben we onderzocht hoe je 10 tot en met de 5 kunt uitdrukken^eMacht, wat betekent dat je 10 vijf keer met zichzelf vermenigvuldigt; het resultaat, 100.000, is een fundamentele waarde die in verschillende contexten voorkomt, zoals de wetenschappelijke notatie, het omzetten van eenheden en binaire getalsystemen. Door het concept van exponentiële notatie en de praktische toepassingen ervan te begrijpen, kunnen we de kracht en overvloed (aanwezigheid) van de wiskunde in het dagelijks leven beter begrijpen.