Topologische sortering voor Gerichte acyclische grafiek (DAG) is een lineaire ordening van hoekpunten zodat voor elke gerichte rand u-v, hoekpunt in komt voor in bij de bestelling.
Opmerking: Topologische sortering voor een grafiek is niet mogelijk als de grafiek niet a is DAG .
npm cache leegmaken
Voorbeeld:
Aanbevolen praktijkOp DFS gebaseerde oplossing om een topologische sortering te vinden is al besproken.Invoer: Grafiek:
Voorbeeld
Uitgang: 5 4 2 3 1 0
Uitleg: Het eerste hoekpunt bij topologische sortering is altijd een hoekpunt met een in-graad van 0 (een hoekpunt zonder inkomende randen). Een topologische sortering van de volgende grafiek is 5 4 2 3 1 0. Er kan meer dan één topologische sortering voor een grafiek zijn. Een andere topologische sortering van de volgende grafiek is 4 5 2 3 1 0.
Topologische volgorde is mogelijk niet uniek:
Topologische sortering is een afhankelijkheidsprobleem waarbij de voltooiing van één taak afhangt van de voltooiing van verschillende andere taken waarvan de volgorde kan variëren. Laten we dit concept begrijpen via een voorbeeld:
Stel dat het onze taak is om onze school te bereiken en om daar te komen, moeten we ons eerst aankleden. De afhankelijkheid van het dragen van kleding wordt weergegeven in de onderstaande afhankelijkheidsgrafiek. Je kunt bijvoorbeeld geen schoenen dragen voordat je sokken draagt.
Uit de bovenstaande afbeelding zou je je al hebben gerealiseerd dat er meerdere manieren zijn om je aan te kleden, de onderstaande afbeelding toont enkele van die manieren.
Kun je een lijst maken alle mogelijke topologische ordening van het aankleden voor bovenstaande afhankelijkheidsgrafiek?
Algoritme voor topologische sortering met behulp van DFS:
Hier is een stapsgewijs algoritme voor topologische sortering met behulp van Depth First Search (DFS):
- Maak een grafiek met N hoekpunten en M -gerichte randen.
- Initialiseer een stapel en een bezochte array van grootte N .
- Voor elk niet-bezocht hoekpunt in de grafiek doet u het volgende:
- Roep de DFS-functie aan met het hoekpunt als parameter.
- Markeer in de DFS-functie het hoekpunt als bezocht en roep recursief de DFS-functie aan voor alle niet-bezochte buren van het hoekpunt.
- Zodra alle buren zijn bezocht, duwt u het hoekpunt op de stapel.
- Er zijn immers hoekpunten bezocht, haal elementen uit de stapel en voeg ze toe aan de uitvoerlijst totdat de stapel leeg is.
- De resulterende lijst is de topologisch gesorteerde volgorde van de grafiek.
Illustratie topologisch sorteeralgoritme:
Onderstaande afbeelding is een illustratie van de bovenstaande aanpak:

Algemene workflow van topologische sortering
Stap 1:
- We starten DFS vanaf knooppunt 0 omdat er geen binnenkomende knooppunten zijn
- We duwen knooppunt 0 in de stapel en gaan naar het volgende knooppunt met een minimum aantal aangrenzende knooppunten, d.w.z. knooppunt 1.
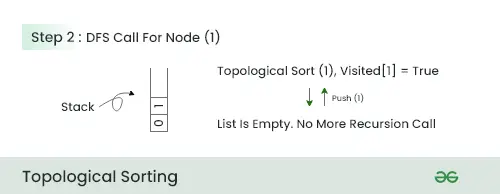
Stap 2:
- Omdat er in deze stap geen aangrenzend knooppunt is, drukt u op knooppunt 1 in de stapel en gaat u naar het volgende knooppunt.
Stap 3:
- In deze stap kiezen we knooppunt 2 omdat dit een minimumaantal aangrenzende knooppunten heeft na 0 en 1.
- We roepen DFS aan voor knooppunt 2 en pushen alle knooppunten die vanaf knooppunt 2 in omgekeerde volgorde komen.
- Dus druk op 3 en vervolgens op 2.
Stap 4:
- We noemen nu DFS voor knooppunt 4
- Omdat 0 en 1 al in de stapel aanwezig zijn, duwen we gewoon knooppunt 4 in de stapel en keren terug.
Stap 5:
- Omdat alle aangrenzende knooppunten van 5 zich al in de stapel bevinden, duwen we in deze stap knooppunt 5 in de stapel en keren terug.
Stap 6: Dit is de laatste stap van de topologische sortering, waarbij we alle elementen uit de stapel halen en in die volgorde afdrukken.
probeer catchblock eens in java
Hieronder vindt u de implementatie van de bovenstaande aanpak:
C++ #include using namespace std; // Function to perform DFS and topological sorting void topologicalSortUtil(int v, vector>& bijvoeglijk naamwoord, vector & bezocht, stapel & Stack) {// Markeer het huidige knooppunt als bezocht bezocht[v] = true; // Terugkerend voor alle aangrenzende hoekpunten voor (int i: adj[v]) { if (!visited[i]) topologicalSortUtil(i, adj, visit, Stack); } // Duw het huidige hoekpunt naar stapel, waarin het resultaat Stack.push(v) wordt opgeslagen; } // Functie om topologische sortering uit te voeren void topologicalSort(vector>& bijvoeglijk naamwoord, int V) { stapel Stapel; // Stapel om de resultaatvector op te slaan bezocht(V, false); // Roep de recursieve helperfunctie op om op te slaan // Topologische sortering beginnend bij alle hoekpunten één voor // één voor (int i = 0; i< V; i++) { if (!visited[i]) topologicalSortUtil(i, adj, visited, Stack); } // Print contents of stack while (!Stack.empty()) { cout << Stack.top() << ' '; Stack.pop(); } } int main() { // Number of nodes int V = 4; // Edges vector> randen = { { 0, 1 }, { 1, 2 }, { 3, 1 }, { 3, 2 } }; // Grafiek weergegeven als een aangrenzende lijstvector> bijvoeglijk naamwoord(V); for (auto i: randen) { adj[i[0]].push_back(i[1]); } uit<< 'Topological sorting of the graph: '; topologicalSort(adj, V); return 0; }>
Java import java.util.*; public class TopologicalSort { // Function to perform DFS and topological sorting static void topologicalSortUtil(int v, List> bijvoeglijk naamwoord, boolean[] bezocht, Stack stack) {// Markeer het huidige knooppunt als bezocht bezocht[v] = true; // Terugkerend voor alle aangrenzende hoekpunten voor (int i: adj.get(v)) { if (!visited[i]) topologicalSortUtil(i, adj, visit, stack); } // Duw het huidige hoekpunt naar de stapel, waarin het // resultaat stack.push(v) wordt opgeslagen; } // Functie voor het uitvoeren van Topological Sort static void topologicalSort(List> adj, int V) {// Stack om het resultaat Stack op te slaan stapel = nieuwe stapel(); boolean[] bezocht = nieuwe boolean[V]; // Roep de recursieve helperfunctie op om op te slaan // Topologische sortering beginnend bij alle hoekpunten één // per één voor (int i = 0; i< V; i++) { if (!visited[i]) topologicalSortUtil(i, adj, visited, stack); } // Print contents of stack System.out.print( 'Topological sorting of the graph: '); while (!stack.empty()) { System.out.print(stack.pop() + ' '); } } // Driver code public static void main(String[] args) { // Number of nodes int V = 4; // Edges List> randen = nieuwe ArrayList(); randen.add(Arrays.asList(0, 1)); randen.add(Arrays.asList(1, 2)); randen.add(Arrays.asList(3, 1)); randen.add(Arrays.asList(3, 2)); // Grafiek weergegeven als een aangrenzende lijstlijst> adj = nieuwe ArrayList(V); voor (int i = 0; ik< V; i++) { adj.add(new ArrayList()); } for (List i: randen) { adj.get(i.get(0)).add(i.get(1)); } topologischeSort(adj, V); } }>
Python3 def topologicalSortUtil(v, adj, visited, stack): # Mark the current node as visited visited[v] = True # Recur for all adjacent vertices for i in adj[v]: if not visited[i]: topologicalSortUtil(i, adj, visited, stack) # Push current vertex to stack which stores the result stack.append(v) # Function to perform Topological Sort def topologicalSort(adj, V): # Stack to store the result stack = [] visited = [False] * V # Call the recursive helper function to store # Topological Sort starting from all vertices one by # one for i in range(V): if not visited[i]: topologicalSortUtil(i, adj, visited, stack) # Print contents of stack print('Topological sorting of the graph:', end=' ') while stack: print(stack.pop(), end=' ') # Driver code if __name__ == '__main__': # Number of nodes V = 4 # Edges edges = [[0, 1], [1, 2], [3, 1], [3, 2]] # Graph represented as an adjacency list adj = [[] for _ in range(V)] for i in edges: adj[i[0]].append(i[1]) topologicalSort(adj, V)> C# using System; using System.Collections.Generic; class Program { // Function to perform DFS and topological sorting static void TopologicalSortUtil(int v, List> bijvoeglijk naamwoord, bool[] bezocht, Stack stack) {// Markeer het huidige knooppunt als bezocht bezocht[v] = true; // Terugkerend voor alle aangrenzende hoekpunten foreach(int i in adj[v]) { if (!visited[i]) TopologicalSortUtil(i, adj, visit, stack); } // Duw het huidige hoekpunt naar de stapel, waarin de // resultaatstapel wordt opgeslagen.Push(v); } // Functie om Topological Sort statische leegte uit te voeren TopologicalSort(List> adj, int V) {// Stack om het resultaat Stack op te slaan stapel = nieuwe stapel (); bool[] bezocht = nieuwe bool[V]; // Roep de recursieve helperfunctie op om op te slaan // Topologische sortering beginnend bij alle hoekpunten één // per één voor (int i = 0; i< V; i++) { if (!visited[i]) TopologicalSortUtil(i, adj, visited, stack); } // Print contents of stack Console.Write('Topological sorting of the graph: '); while (stack.Count>0) { Console.Write(stack.Pop() + ''); } } // Stuurprogrammacode static void Main(string[] args) {// Aantal knooppunten int V = 4; // Randenlijst> randen = nieuwe lijst>{ nieuwe lijst { 0, 1 }, nieuwe lijst { 1, 2 }, nieuwe lijst { 3, 1 }, nieuwe lijst { 3, 2 } }; // Grafiek weergegeven als een aangrenzende lijstlijst> bijvoeglijk naamwoord = nieuwe lijst>(); voor (int i = 0; ik< V; i++) { adj.Add(new List ()); } foreach(Lijst i in randen) { adj[i[0]].Add(i[1]); } TopologischeSort(adj, V); } }>
Javascript // Function to perform DFS and topological sorting function topologicalSortUtil(v, adj, visited, stack) { // Mark the current node as visited visited[v] = true; // Recur for all adjacent vertices for (let i of adj[v]) { if (!visited[i]) topologicalSortUtil(i, adj, visited, stack); } // Push current vertex to stack which stores the result stack.push(v); } // Function to perform Topological Sort function topologicalSort(adj, V) { // Stack to store the result let stack = []; let visited = new Array(V).fill(false); // Call the recursive helper function to store // Topological Sort starting from all vertices one by // one for (let i = 0; i < V; i++) { if (!visited[i]) topologicalSortUtil(i, adj, visited, stack); } // Print contents of stack console.log('Topological sorting of the graph: '); while (stack.length>0) {console.log(stack.pop() + ''); } } // Stuurprogrammacode (() => { // Aantal knooppunten const V = 4; // Randen const randen = [[0, 1], [1, 2], [3, 1], [3, 2]]; // Grafiek weergegeven als een aangrenzende lijst const adj = Array.from({ lengte: V }, () => []); (i[1]); } topologischeSort(adj, V);> Uitvoer
Topological sorting of the graph: 3 0 1 2>
Tijdcomplexiteit: O(V+E). Het bovenstaande algoritme is eenvoudigweg DFS met een extra stapel. Tijdcomplexiteit is dus hetzelfde als DFS
Hulpruimte: O(V). De extra ruimte is nodig voor de stapel
Topologische sortering met behulp van BFS:
C++ #include #include #include using namespace std; // Class to represent a graph class Graph { int V; // No. of vertices list * bijvoeglijk naamwoord; // Wijzer naar een array met // aangrenzende lijsten public: Graph(int V); // Constructor void addEdge(int v, int w); // Functie om een rand toe te voegen aan de grafiek void topologicalSort(); // drukt een topologische soort af van // de volledige grafiek }; Grafiek::Grafiek(int V) { this->V = V; adj = nieuwe lijst [V]; } void Graph::addEdge(int v, int w) { adj[v].push_back(w); // Voeg w toe aan de lijst van v. } // Functie om topologische sortering uit te voeren void Graph::topologicalSort() {// Maak een vector om alle hoekpuntenvector in graden op te slaan in_graad(V, 0); // Doorkruis aangrenzende lijsten om_graad van // hoekpunten in te vullen voor (int v = 0; v< V; ++v) { for (auto const& w : adj[v]) in_degree[w]++; } // Create a queue and enqueue all vertices with // in-degree 0 queue Q; voor (int i = 0; ik< V; ++i) { if (in_degree[i] == 0) q.push(i); } // Initialize count of visited vertices int count = 0; // Create a vector to store topological order vector top_bestelling; // Een voor een dequeue-hoekpunten uit de wachtrij en in de wachtrij plaatsen // aangrenzende hoekpunten als de in-graad van aangrenzend 0 wordt terwijl (!q.empty()) {// Extraheer de voorkant van de wachtrij (of voer dequeue uit) // en voeg deze toe aan topologische volgorde int u = q.front(); q.pop(); top_order.push_back(u); // Herhaal alle aangrenzende knooppunten // van het uit de wachtrij geplaatste knooppunt u en verlaag hun graad // met 1 lijst ::iterator itr; for (itr = adj[u].begin(); itr != adj[u].end(); ++itr) // Als in-degree nul wordt, voeg het dan toe aan de wachtrij if (--in_degree[*itr ] == 0) q.push(*itr); tellen++; } // Controleer of er een cyclus was if (count != V) { cout<< 'Graph contains cycle
'; return; } // Print topological order for (int i : top_order) cout << i << ' '; } // Driver code int main() { // Create a graph given in the above diagram Graph g(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); cout << 'Following is a Topological Sort of the given ' 'graph
'; g.topologicalSort(); return 0; }> Java import java.util.ArrayList; import java.util.LinkedList; import java.util.Queue; // Class to represent a graph class Graph { private int V; // No. of vertices private ArrayList [] bijvoeglijk naamwoord; // Aangrenzende lijst // weergave van // de grafiek // Constructorgrafiek (int V) { this.V = V; adj = nieuwe ArrayList[V]; voor (int i = 0; ik< V; ++i) adj[i] = new ArrayList(); } // Function to add an edge to the graph void addEdge(int v, int w) { adj[v].add(w); // Add w to v’s list. } // Function to perform Topological Sort void topologicalSort() { // Create an array to store in-degree of all // vertices int[] inDegree = new int[V]; // Calculate in-degree of each vertex for (int v = 0; v < V; ++v) { for (int w : adj[v]) { inDegree[w]++; } } // Create a queue and enqueue all vertices with // in-degree 0 Queue q = nieuwe LinkedList(); voor (int i = 0; ik< V; ++i) { if (inDegree[i] == 0) q.add(i); } // Initialize count of visited vertices int count = 0; // Create an ArrayList to store topological order ArrayList topOrder = nieuwe ArrayList(); // Haal de hoekpunten één voor één uit de wachtrij en // plaats aangrenzende hoekpunten in de wachtrij als de graad van // aangrenzend 0 wordt terwijl (!q.isEmpty()) {/ // Extraheer de voorkant van de wachtrij en voeg deze toe aan // topologische volgorde int u = q.poll(); topOrder.add(u); tellen++; // Doorloop al zijn aangrenzende knooppunten van // uit de wachtrij gehaald knooppunt u en verlaag hun in-degree // met 1 voor (int w: adj[u]) {/ // Als in-degree nul wordt, voeg het toe aan // wachtrij if (--inDegree[w] == 0) q.add(w); } } // Controleer of er een cyclus was if (count != V) { System.out.println('Grafiek bevat cyclus'); opbrengst; } // Print topologische volgorde voor (int i: topOrder) System.out.print(i + ' '); } } // Stuurprogrammacode public class Main { public static void main(String[] args) {// Maak een grafiek uit het bovenstaande diagram Graph g = new Graph(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); System.out.println( 'Het volgende is een topologische sortering van de gegeven grafiek'); g.topologicalSort(); } }> Python3 from collections import defaultdict class Graph: def __init__(self, vertices): # Number of vertices self.V = vertices # Dictionary to store adjacency lists self.adj = defaultdict(list) def addEdge(self, u, v): # Function to add an edge to the graph self.adj[u].append(v) def topologicalSort(self): # Function to perform Topological Sort # Create a list to store in-degree of all vertices in_degree = [0] * self.V # Traverse adjacency lists to fill in_degree of vertices for i in range(self.V): for j in self.adj[i]: in_degree[j] += 1 # Create a queue and enqueue all vertices with in-degree 0 q = [] for i in range(self.V): if in_degree[i] == 0: q.append(i) # Initialize count of visited vertices count = 0 # Create a list to store topological order top_order = [] # One by one dequeue vertices from queue and enqueue # adjacent vertices if in-degree of adjacent becomes 0 while q: # Extract front of queue (or perform dequeue) # and add it to topological order u = q.pop(0) top_order.append(u) # Iterate through all its neighbouring nodes # of dequeued node u and decrease their in-degree # by 1 for node in self.adj[u]: # If in-degree becomes zero, add it to queue in_degree[node] -= 1 if in_degree[node] == 0: q.append(node) count += 1 # Check if there was a cycle if count != self.V: print('Graph contains cycle') return # Print topological order print('Topological Sort:', top_order) # Driver code if __name__ == '__main__': # Create a graph given in the above diagram g = Graph(6) g.addEdge(5, 2) g.addEdge(5, 0) g.addEdge(4, 0) g.addEdge(4, 1) g.addEdge(2, 3) g.addEdge(3, 1) print('Following is a Topological Sort of the given graph') g.topologicalSort()> JavaScript // Class to represent a graph class Graph { constructor(V) { this.V = V; // No. of vertices this.adj = new Array(V); // Array containing adjacency lists for (let i = 0; i < V; i++) { this.adj[i] = []; } } // Function to add an edge to the graph addEdge(v, w) { this.adj[v].push(w); // Add w to v’s list. } // Function to perform Topological Sort topologicalSort() { // Create a array to store in-degree of all vertices let inDegree = new Array(this.V).fill(0); // Traverse adjacency lists to fill inDegree of vertices for (let v = 0; v < this.V; v++) { for (let w of this.adj[v]) { inDegree[w]++; } } // Create a queue and enqueue all vertices with in-degree 0 let queue = []; for (let i = 0; i < this.V; i++) { if (inDegree[i] === 0) { queue.push(i); } } // Initialize count of visited vertices let count = 0; // Create an array to store topological order let topOrder = []; // One by one dequeue vertices from queue and enqueue // adjacent vertices if in-degree of adjacent becomes 0 while (queue.length !== 0) { // Extract front of queue and add it to topological order let u = queue.shift(); topOrder.push(u); // Iterate through all its neighboring nodes // of dequeued node u and decrease their in-degree by 1 for (let w of this.adj[u]) { // If in-degree becomes zero, add it to queue if (--inDegree[w] === 0) { queue.push(w); } } count++; } // Check if there was a cycle if (count !== this.V) { console.log('Graph contains cycle'); return; } // Print topological order console.log('Topological Sort of the given graph:'); console.log(topOrder.join(' ')); } } // Driver code // Create a graph given in the above diagram let g = new Graph(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); console.log('Following is a Topological Sort of the given graph:'); g.topologicalSort(); //This code is contributed by Utkarsh> Uitvoer
Following is a Topological Sort of the given graph 4 5 2 0 3 1>
Tijdcomplexiteit:
De tijdscomplexiteit voor het construeren van de grafiek is O(V + E), waarbij V het aantal hoekpunten is en E het aantal randen.
De tijdscomplexiteit voor het uitvoeren van topologische sortering met behulp van BFS is ook O(V + E), waarbij V het aantal hoekpunten is en E het aantal randen. Dit komt omdat elk hoekpunt en elke rand één keer wordt bezocht tijdens de BFS-doorgang.
Ruimtecomplexiteit:
De ruimtecomplexiteit voor het opslaan van de grafiek met behulp van een aangrenzende lijst is O(V + E), waarbij V het aantal hoekpunten is en E het aantal randen.
Er wordt extra ruimte gebruikt voor het opslaan van de hoekpunten in de graad, waarvoor O(V)-ruimte nodig is.
Voor BFS-traversal wordt een wachtrij gebruikt, die maximaal V-hoekpunten kan bevatten. De ruimtecomplexiteit voor de wachtrij is dus O(V).
Over het geheel genomen is de ruimtecomplexiteit van het algoritme O(V + E) vanwege de opslag van de grafiek, de in-graden array en de wachtrij.
Samenvattend is de tijdscomplexiteit van de geleverde implementatie O(V + E), en de ruimtecomplexiteit is ook O(V + E).
Opmerking: Hier kunnen we ook een array gebruiken in plaats van de stapel. Als de array wordt gebruikt, drukt u de elementen in omgekeerde volgorde af om de topologische sortering te verkrijgen.
Voordelen van topologische sortering:
- Helpt bij het plannen van taken of gebeurtenissen op basis van afhankelijkheden.
- Detecteert cycli in een gerichte grafiek.
- Efficiënt voor het oplossen van problemen met prioriteitsbeperkingen.
Nadelen van topologische sortering:
- Alleen toepasbaar op gerichte acyclische grafieken (DAG's), niet geschikt voor cyclische grafieken.
- Het hoeft niet uniek te zijn; er kunnen meerdere geldige topologische ordeningen bestaan.
- Inefficiënt voor grote grafieken met veel knooppunten en randen.
Toepassingen van topologische sortering:
- Taakplanning en projectmanagement.
- Afhankelijkheidsresolutie in pakketbeheersystemen.
- Bepalen van de compilatievolgorde in softwarebouwsystemen.
- Deadlock-detectie in besturingssystemen.
- Cursusplanning op universiteiten.
Gerelateerde artikelen:
- Kahn's algoritme voor topologische sortering
- Alle topologische soorten van een gerichte acyclische grafiek