Trigonometrie is een belangrijke tak van de wiskunde die zich bezighoudt met de relatie tussen hoeken en lengtes van de zijden van een rechthoekige driehoek. De zes trigonometrische verhoudingen of functies zijn sinus, cosinus, tangens, cosecans en secans, en een trigonometrische verhouding is een verhouding tussen de zijden van een rechthoekige driehoek. Sinus-, cosinus- en tangensfuncties zijn drie belangrijke trigonometrische functies, aangezien de andere drie, dat wil zeggen cosecans-, secans- en cotangensfuncties, de wederzijdse functies zijn van respectievelijk sinus-, cosinus- en tangensfuncties.
- sin θ = tegenoverliggende zijde/hypotenusa
- cos θ = aangrenzende zijde/hypotenusa
- tan θ = tegenoverliggende zijde/aangrenzende zijde
- cosec θ = Hypotenusa/tegenoverliggende zijde
- sec θ = hypotenusa/aangrenzende zijde
- kinderbedje θ = aangrenzende zijde/tegenoverliggende zijde
De tangensfunctie is een van de zes trigonometrische functies die worden gebruikt trigonometrieformules .
Inhoudsopgave
Tangens formule
De raaklijn van een hoek in een rechthoekige driehoek is de verhouding tussen de lengte van de tegenoverliggende zijde en de lengte van de aangrenzende zijde van de gegeven hoek. We schrijven een tangensfunctie als tan. Laten we een rechthoekige driehoek XYZ bekijken en een van zijn scherpe hoeken is θ. Een tegenoverliggende zijde is de zijde die tegenovergesteld is aan de hoek θ en de aangrenzende zijde is de zijde die grenst aan de hoek θ.
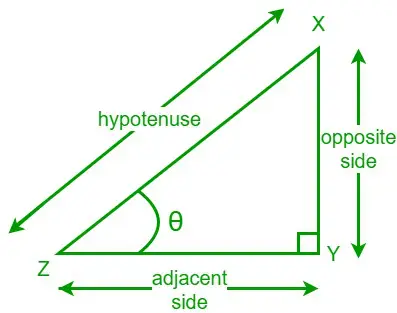
De raaklijnformule voor de gegeven hoek θ is nu:
tan θ = tegenoverliggende zijde/aangrenzende zijde
Enkele basistangensformules
Raaklijnfunctie in kwadranten
De raaklijnfunctie is positief in het eerste en derde kwadrant en negatief in het tweede en vierde kwadrant.
- bruinen (2π + θ) = bruinen θ (1stkwadrant)
- bruin (π – θ) = – bruin θ (2nlkwadrant)
- bruinen (π + θ) = bruinen θ (3rdkwadrant)
- bruin (2π – θ) = – bruin θ (4ekwadrant)
Raaklijnfunctie als negatieve functie
De tangensfunctie is een negatieve functie omdat de tangens van een negatieve hoek het negatief is van een positieve tangenshoek.
bruin (-θ) = – bruin θ
Raaklijnfunctie in termen van sinus- en cosinusfunctie
De raaklijnfunctie in termen van sinus- en cosinusfuncties kan worden geschreven als:
tan θ = sin θ/cos θ
Dat weten we, tan θ = tegenoverliggende zijde/aangrenzende zijde
Deel nu zowel de teller als de noemer door de hypotenusa
tan θ = (tegenoverliggende zijde/hypotenusa)/(aangrenzende zijde/hypotenusa)
Dat weten we, sin θ = tegenoverliggende zijde/hypotenusa
cos θ = aangrenzende zijde/hypotenusa
Dus tan θ = sin θ/cos θ
Raaklijnfunctie in termen van sinusfunctie
De raaklijnfunctie in termen van de sinusfunctie kan worden geschreven als:
tan θ = zonde θ/(√1 – zonde 2 i)
We weten dat,
tan θ = sin θ/cos θ
wat betekent dit xd
Van de identiteiten van Pythagoras hebben we:
zonder2θ + cos2θ = 1
want2θ = 1 – zonde2i
cos θ = √(1 – zonde2i)
Dus tan θ = zonde θ/(√1 – zonde2i)
Raaklijnfunctie in termen van cosinusfunctie
De raakfunctie in termen van de cosinusfunctie kan worden geschreven als:
bruin θ = (√1 -cos 2 ik)/cos ik
We weten dat,
tan θ = sin θ/cos θ
Van de identiteiten van Pythagoras hebben we:
zonder2θ + cos2θ = 1
zonder2θ = 1 – cos2i
zonde θ = √(1 – cos2i)
Dus tan θ = (√1 – cos2ik)/cos ik
Tangensfunctie in termen van cotangensfunctie
De raakfunctie in termen van de cotangensfunctie kan worden geschreven als:
bruin θ = 1/kinderbedje θ
of
bruin θ = kinderbed (90° – θ) (of) kinderbed (π/2 – θ)
Raaklijnfunctie in termen van cosecante functie
De raakfunctie in termen van de cosecante functie kan worden geschreven als:
bruin θ = 1/√(cosec 2 ik – 1)
Van de identiteiten van Pythagoras hebben we:
cosec2θ – kinderbed2θ = 1
kinderbed2θ = cosec2ik – 1
kinderbedje θ = √(cosec2ik – 1)
We weten dat,
bruin θ = 1/kinderbedje θ
Daarom is tan θ = 1/√(cosec2ik – 1)
Raaklijnfunctie in termen van secansfunctie
De raaklijnfunctie in termen van de secansfunctie kan worden geschreven als:
bruin θ = √sec 2 ik – 1
Van de identiteiten van Pythagoras hebben we:
sec2θ – dus2θ = 1
bruin θ = sec2ik – 1
Daarom is tan θ = √(sec2ik – 1)
Raaklijnfunctie in termen van dubbele hoek
Raaklijnfunctie voor een dubbele hoek is,
bruin 2θ = (2 bruin θ)/(1 – bruin 2 i)
Raaklijnfunctie in termen van drievoudige hoek
Raaklijnfunctie voor een drievoudige hoek is,
bruin 3θ = (3 bruin θ – bruin 3 θ) / (1 – 3 bruinen 2 i)
Raaklijnfunctie in termen van halve hoek
Tangensfunctie voor een halve hoek is,
bruin (θ/2) = ± √[ (1 – cos θ) / (1 + cos θ) ]
bruin (θ/2) = (1 – cos θ) / ( sin θ)
Raaklijnfunctie in termen van optellen en aftrekken van twee hoeken
Som- en verschilformules voor een raaklijnfunctie zijn:
bruin (A + B) = (bruin A + bruin B)/(1 – bruin A bruin B)
bruin (A – B) = (bruin A – bruin B)/(1 + bruin A bruin B)
Trigonometrische verhoudingstabel
| Hoek (in graden) | Hoek (in radialen) | zonde ik | cos θ | tan θ = sin θ/cos θ | cosec θ | sec θ | kinderbedje ik |
|---|---|---|---|---|---|---|---|
| 0° | 0 | 0 | 1 | 0/1 = 0 | Ongedefinieerd | 1 | Ongedefinieerd |
| 30° | p/6 | 1/2 | √3/2 | (1/2)/(√3/2) = 1/√3 | 2 | 23 | √3 |
| 45° | p/4 | 1/√2 | 1/√2 | (1/√2)/(1/√2) = 1 | √2 | √2 | 1 |
| 60° | p/3 | √3/2 | 1/2 | (√3/2)/(1/2) = √3 latex lijst | 23 | 2 | 1/√3 |
| 90° | p/2 | 1 | 0 | 1/0 = ongedefinieerd | 1 | Ongedefinieerd | 0 |
| 120° | 2p/3 | √3/2 | -1/2 | (√3/2)/(-1/2) = -√3 | 23 | -2 | -1/√3 |
| 150° | 5p/6 | 1/2 | -(√3/2) | (1/2)/(-√3/2) = -1/√3 | 2 | -(23) | -√3 |
| 180° | Pi | 0 | -1 | 0/(-1) = 0 | Ongedefinieerd | -1 | Ongedefinieerd |
Opgelost voorbeeld van raaklijnformules
Voorbeeld 1: Vind de waarde van tan θ als sin θ = 2/5 en θ de hoek van het eerste kwadrant is.
Oplossing:
Gegeven,
- zonde θ = 2/5
Van de Pythagoras-identiteiten die we hebben,
zonder2θ + cos2θ = 1
want2θ = 1 – zonde2θ = 1 – (2/5)2
want2θ = 1 – (4/5) = 21/25
cos θ = ±√21/5
Omdat θ de hoek van het eerste kwadrant is, is cos θ positief.
cos θ = √21/5
We weten dat,
tan θ = sin θ/cos θ
= (2/5)/(√21/5) = 2/√21
bruin θ = 2√21 /21
Dus de waarde van tan θ wanneer sin θ = 2/5 en θ zich in het eerste kwadrant bevindt, is (2√21) /(21)
Voorbeeld 2: Vind de waarde van tan x als sec x = 13/12 en x de hoek van het vierde kwadrant is.
Oplossing:
Gegeven, sec x = 13/12
Van de identiteiten van Pythagoras hebben we:
sec2x-zo2x = 1
Dus2x = sec2x – 1= (13/12)2- 1
conversie van datum naar tekenreeksDus2x = (169/144) – 1= 25/144
bruin x = ± 5/12
Omdat x de hoek van het vierde kwadrant is, is tan x negatief.
bruin x = – 5/12
Vandaar, bruin x = – 5/12
Voorbeeld 3: Als tan X = 2/3 en tan Y = 1/2, wat is dan de waarde van tan (X + Y)?
Oplossing:
Gegeven,
bruin X = 2/3 en bruin Y = 1/2
We weten dat,
bruin (X + Y) = (bruin X + bruin Y)/(1 – bruin X bruin Y)
bruin (X + Y) = [(2/3) + (1/2)]/[1 – (2/3)×(1/2)]
= (7/6)/(2/3) = 7/4
Vandaar, bruin(X + Y) = 7/4
Voorbeeld 4: Bereken de raaklijnfunctie als de aangrenzende en tegenoverliggende zijden van een rechthoekige driehoek respectievelijk 4 cm en 7 cm zijn.
Oplossing:
Gegeven,
Aangrenzende zijde = 4 cm
Tegengestelde kant = 7 cm
We weten dat,
tan θ = tegenoverliggende zijde/aangrenzende zijde
bruin θ = 7/4 = 1,75
Vandaar, bruin θ = 1,75
Voorbeeld 5: Een man kijkt naar een klokkentoren in een hoek van 60° ten opzichte van de top van de toren, die 100 meter hoog is. Wat is de afstand tussen de man en de voet van de toren?
Oplossing:
Gegeven,
Hoogte toren = 100 m en θ = 60°
Stel dat de afstand tussen de mens en de voet van de toren = d
We hebben,
tan θ = tegenoverliggende zijde/aangrenzende zijde
bruin 60° = 100/d
√3 = 100/d [Sinds, dus 60° = √3]
d = 100/√3
Daarom is de afstand tussen de man en de voet van de toren gelijk 100/√3
Voorbeeld 6: Vind de waarde van tan θ als sin θ = 7/25 en sec θ = 25/24.
Oplossing:
Gegeven,
zonde θ = 7/25
sec θ = 25/24
We weten dat,
sec θ = 1/cos θ
25/24 = 1/cos θ cos θ = 24/25
We hebben,
tan θ = sin θ/cos θ
= (25/7)/(24/25)
= 24/7
Vandaar, bruin θ = 7/24
Voorbeeld 7: Vind de waarde van tan θ als cosec θ = 5/3, en θ de hoek van het eerste kwadrant is.
Oplossing:
Gegeven: cosec θ = 5/3
Van de identiteiten van Pythagoras hebben we:
string.format javacosec2θ – kinderbed2θ = 1
kinderbed2θ = cosec2ik – 1
kinderbedje θ = (5/3)2– 1 = (25/9) – 1 = 16/9
kinderbedje θ = ±√16/9 = ± 4/3
Omdat θ de eerste kwadranthoek is, zijn zowel de cotangens- als de tangensfuncties positief.
kinderbedje θ = 4/3
We weten dat,
kinderbed θ = 1/bruin θ
4/3 = 1/tanθ
bruin θ = 3/4
Vandaar, bruin θ = 3/4
Voorbeeld 8: Vind tan 3θ als sin θ = 3/7 en θ de hoek van het eerste kwadrant is.
Oplossing :
Gegeven, zonde θ = 12/13
Van de Pythagoras-identiteiten die we hebben,
zonder2θ + cos2θ = 1
want2θ = 1 – zonde2θ = 1 – (12/13)2
cos2 θ = 1 – (144/169) = 25/169
cos θ = ±√25/169 = ±5/13
Omdat θ de hoek van het eerste kwadrant is, is cos θ positief.
cos θ = 5/13
We weten dat,
tan θ = sin θ/cos θ
= (25/12)/(5/13) = 12/5
Daarom is tan θ = 12/5
Nu weten we dat,
bruin 3θ = (3 bruin θ – bruin3θ) / (1 – 3 bruin2θ)
bruin 3θ = 3 × (12/5)

