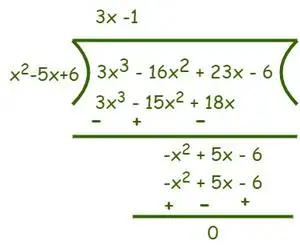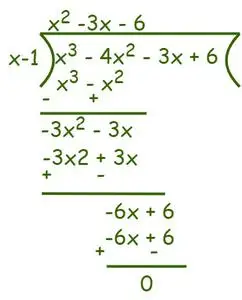Kubieke vergelijking is een wiskundige vergelijking waarin een polynoom van graad 3 wordt gelijkgesteld aan een constante of een ander polynoom van maximale graad 2. De standaardweergave van de derdegraadsvergelijking is bijl 3 +bx 2 +cx+d = 0 waarbij a, b, c en d reële getallen zijn. Enkele voorbeelden van kubieke vergelijking zijn X 3 – 4x 2 + 15x – 9 = 0, 2x 3 – 4x 2 = 0 enz.
Inhoudsopgave
- Polynomiale definitie
- Mate van vergelijking
- Kubieke vergelijkingsdefinitie
- Hoe kubieke vergelijkingen op te lossen?
- Kubieke vergelijkingen oplossen
- Kubieke vergelijkingen oplossen met behulp van factoren
- Kubieke vergelijkingen oplossen met behulp van een grafische methode
- Problemen gebaseerd op het oplossen van kubieke vergelijkingen
- Oefenproblemen bij het oplossen van kubieke vergelijkingen
Om te leren hoe we kubieke vergelijkingen kunnen oplossen, moeten we eerst leren over polynomen, de graad van de polynoom en andere. In dit artikel zullen we in detail leren over veeltermen, veeltermvergelijkingen, het oplossen van kubische vergelijkingen of het oplossen van kubische vergelijkingen.
Polynomiale definitie
Polynoom wordt als volgt gedefinieerd:
A polynoom is een algebraïsche uitdrukking waarin de macht van een variabele een niet-negatief geheel getal is. De algemene vorm van een polynoom is a0XN+ een1Xn-1+ een2Xn-2+… + eenN. Afhankelijk van het maximale vermogen van de variabele kan een polynoom worden geclassificeerd als monomiaal, binomiaal, trinomiaal, enzovoort.
Wat is een vergelijking?
Een vergelijking wordt als volgt gedefinieerd:
Een vergelijking is een polynoom dat wordt gelijkgesteld aan een numerieke waarde of een ander polynoom. X + 2 is bijvoorbeeld een polynoom, maar x + 2 = 5 is een vergelijking. Op dezelfde manier is 2x + 3 = x + 1 ook een vergelijking, terwijl 2x + 3 en x + 1 afzonderlijk polynomen zijn.
Mate van vergelijking
De definitie van de graad van vergelijking wordt hieronder vermeld:
Mate van een vergelijking wordt gedefinieerd als het maximale vermogen dat de variabele in een vergelijking bezit.
Op basis van de mate van de vergelijking kan een vergelijking als volgt worden geclassificeerd:
- Lineaire vergelijking
- Kwadratische vergelijking
- Kubieke vergelijking
- Bikwadratische vergelijking
Lineaire vergelijking
De vergelijking waarbij het maximale vermogen van de variabele 1 is, wordt een lineaire vergelijking genoemd.
- Bijvoorbeeld 3x +1 = 0
Kwadratisch polynoom
De vergelijking waarbij het maximale vermogen van de variabele 2 is, is een kwadratische vergelijking.
- Bijvoorbeeld 3x2+x+1 = 0
Kubieke vergelijking
De vergelijking waarbij het maximale vermogen van de variabele 3 is, wordt een kubieke vergelijking genoemd.
- Bijvoorbeeld 5x3+3x2+x+1 = 0
Bikwadratisch polynoom
De vergelijking waarin het maximale vermogen van de variabele 4 is, wordt een bikwadratisch polynoom of kwartisch polynoom genoemd.
- Bijvoorbeeld 5x4+4x3+3x2+2x+1 = 0
Kubieke vergelijkingsdefinitie
Kubieke vergelijking is een algebraïsche vergelijking waarbij de hoogste graad van de polynoom 3 is. Enkele voorbeelden van derdegraadsvergelijkingen zijn 5x3+3x2+x+1 = 0, 2x3+8 = x ⇒ 2x3-x+8 = 0, enz.
De algemene vorm van een derdegraadsvergelijking is:
bijl 3 + bx 2 + cx + d = 0, a ≠ 0
Waar,
- een, b, En C zijn de coëfficiënten van de variabele en hun exponenten en D is de constante, en
- a, b, c En D zijn echte cijfers.
Hoe kubieke vergelijkingen op te lossen?
Een derdegraadsvergelijking is een vergelijking met graad drie. Het heeft drie oplossingen en kan eenvoudig worden opgelost door de onderstaande stappen te volgen:
Stap 1: Vind één oplossing voor de derdegraadsvergelijking via de hit-and-try-methode. Stel dat we een derdegraadsvergelijking P(x) hebben en zoek dan voor elke x = a, P(a) = 0 door te nemen: x = 0, ±1, ±2, ±3, … enzovoort.
Stap 2: Als we P(a) = 0 krijgen, zoek dan de factor (x – a) van P(x)
Stap 3: Deel P(x) door (x – a) om een kwadratische vergelijking te krijgen, bijvoorbeeld Q(x), met behulp van polynomiale deling.
Stap 4: Factariseer de kwadratische vergelijking Q(x) om de factoren (x – b) en (x – c) te verkrijgen.
Stap 5: (x – a), (x – b) en (x – c) zijn de factoren van P(x) en als we elke factor oplossen, krijgen we de wortels van vergelijking als, a, b en c.
sorteren in arraylist in Java
Leer meer over, Verdelende veelterm
Kubieke vergelijkingen oplossen
A Kubieke vergelijking kan op twee manieren worden opgelost
- Door het te reduceren tot een kwadratische vergelijking en deze vervolgens op te lossen door middel van factoring of de kwadratische formule
- Via grafische methode
A Kubieke vergelijking heeft drie wortels. Deze wortels kunnen reëel of denkbeeldig zijn. Er kunnen ook verschillende wortels zijn, of twee dezelfde en één verschillende wortel en alle drie dezelfde wortels.
Er moet worden opgemerkt dat voor elke vergelijking, inclusief Kubieke vergelijkingen , moet de vergelijking altijd eerst in de standaardvorm worden gerangschikt voordat de vergelijking wordt opgelost.
Als de gegeven vergelijking bijvoorbeeld 2x is2-5 = x + 4/x, dan moeten we dit herschikken naar de standaardvorm, d.w.z. 2x3-X2-5x-4 = 0. Nu kunnen we de vergelijking oplossen met elke geschikte methode.
Kubieke vergelijkingen oplossen met behulp van factoren
De oplossing van de derdegraadsvergelijking met behulp van de factorstelling wordt uitgelegd aan de hand van het onderstaande voorbeeld:
Voorbeeld: Vind de wortels van vergelijking f(x) = 3x 3 −16x 2 + 23x − 6 = 0.
Oplossing:
Gegeven uitdrukking: f(x) = 3x3−16x2+ 23x − 6 = 0
Ontbind eerst de polynoom in factoren om wortels te krijgen
Omdat de constante -6 is, zijn de mogelijke factoren 1, 2, 3, 6
f(1) = 3 – 16 + 23 – 6 ≠ 0
f(2) = 24 – 64 + 46 – 6 = 0
f(3) = 81 – 144 + 69 – 6 = 0
f(6) = 648 – 576 + 138 – 6 ≠ 0
Dat weten wij, volgens Factorstelling als f(a) = 0, dan is (x-a) een factor van f(x)
Dus (x – 2) en (x – 3) zijn factoren van f(x). Daarom zal het product van (x – 2) en (x – 3) ook een factor zijn van f(x). Om nu de resterende factoren te vinden, gebruikt u de staartdelingmethode en deelt u f(x) door het product van (x – 2) en (x – 3)
Daarom is deler = (x – 2)(x – 3) = (x2– 5x + 6) en Dividend = 3x3−16x2+ 23x − 6. Deel nu zoals hieronder weergegeven,
Na deling verkrijgen we (3x-1) als quotiënt en de rest is 0. Nu volgens Divisie-algoritme we weten dat Dividend = Deler×Quotiënt+Restant.
⇒ f(x) = (3x3−16x2+ 23x − 6) = (x2– 5x + 6)(3x-1)
Omdat f(x) = 0
⇒ (x2– 5x + 6)(3x-1) = 0
⇒ x2– 5x + 6 = 0 of 3x-1 = 0
Nu nemen we 3x-1 = 0 ⇒ x = 1/3 omdat we al twee wortels uit x kennen2– 5x + 6, wat 2 en 3 is
Dus,
Wortels van het gegeven Kubieke vergelijking zijn 1/3, 2 en 3.
Kubieke vergelijkingen oplossen met behulp van een grafische methode
Een derdegraadsvergelijking wordt grafisch opgelost als u de gegeven vergelijking niet met andere technieken kunt oplossen. We hebben dus een nauwkeurige tekening van de gegeven derdegraadsvergelijking nodig. De wortels van de vergelijking zijn het punt(en) waarop de grafiek de X-as kruist als de vergelijking in termen van x is en als de vergelijking in termen van y is, dan zijn de wortels van de vergelijking de punten waarop de grafiek snijdt de Y-as.
Het aantal reële oplossingen voor de derdegraadsvergelijking is gelijk aan het aantal keren dat de grafiek van de derdegraadsvergelijking de X-as kruist.
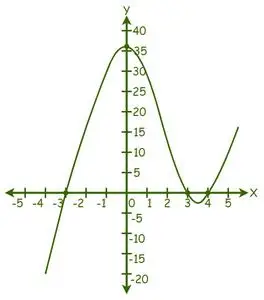
Voorbeeld: Vind de wortels van vergelijking f(x) = x 3 − 4x 2 − 9x + 36 = 0, met behulp van de grafische methode.
Oplossing:
Gegeven uitdrukking: f(x) = x3− 4x2− 9x + 36 = 0.
Vervang nu eenvoudig willekeurige waarden voor x in de grafiek voor de gegeven functie:
X
-4
-3
-2
-1
0
1
2
3
4
5
f(x)
-56
0
19
40
36
24
10
0
0
16
We kunnen zien dat de grafiek de X-as op 3 punten heeft doorgesneden, dus er zijn 3 echte oplossingen.
Uit de grafiek zijn de oplossingen: x = -3, x = 3 en x = 4.
Daarom zijn de wortels van de gegeven vergelijking -3, 3 en 4.
Lees verder,
- Lineaire vergelijking
- Kwadratische vergelijking oplossen
- Veeltermen in factoren ontbinden
Problemen gebaseerd op het oplossen van kubieke vergelijkingen
Probleem 1: Vind de wortels van f(x) = x 3 – 4x 2 -3x + 6 = 0.
Oplossing:
Gegeven uitdrukking: f(x) = x3– 4x2-3x + 6 = 0.
Ontbind eerst de polynoom in factoren om wortels te krijgen.
Omdat de constante +6 is, zijn de mogelijke factoren 1, 2, 3, 6.
f(1) = 1 – 4 – 3 + 6 = 7 – 7 = 0
f(2) = 8 – 16 – 6 + 6 ≠ 0
f(3) = 27 – 36 – 9 + 6 ≠ 0
f(6) = 216 – 144 -18 + 6 = -48 ≠ 0
Dus volgens Factorstelling (x – 1) is een factor van de gegeven vergelijking. Gebruik nu de staartdelingsmethode om de resterende factoren te vinden.
Volgens Divisie-algoritme we kunnen schrijven,
Dus f(x) = x3– 4x2-3x + 6 = (x – 1) (x2– 3x – 6) = 0
⇒ (x – 1) = 0 of (x2– 3x – 6) = 0
We weten dat de wortels van een kwadratische vergelijking ax2+ bx + c = 0 zijn,
x = [-b ± √(b2-4ac)]/2a
Daarom is voor (x2– 3x – 6) = 0
x = [3 ± √(32– 4(1)(-6)]/2(1)
x = (3 ± √33)/2
De wortels van de gegeven derdegraadsvergelijking zijn dus 1, (3+√33)/2 en (3–√33)/2.
Probleem 2: Vind de wortels van vergelijking f(x) = 4x 3 – 10x 2 + 4x = 0.
Oplossing:
Gegeven uitdrukking: f(x) = 4x3– 10x2+ 4x = 0
⇒x(4x2– 10x + 4) = 0
⇒x(4x2– 8x – 2x + 4) = 0
⇒ x(4x(x – 2) – 2(x – 2)) = 0
⇒ x (4x – 2) (x – 2) = 0
⇒ x = 0 of 4x – 2 = 0, x – 2 = 0
⇒ x = 0 of x = 1/2 of x = 2
De wortels van de gegeven vergelijking zijn dus 0, 1/2 en 2.
Probleem 3: Vind de wortels van vergelijking f(x) = x 3 + 3x 2 + x + 3 = 0.
Oplossing:
Gegeven uitdrukking: f(x) = x3+ 3x2+ x + 3 = 0.
⇒ x2(x+3) + 1(x+3) = 0
⇒ (x + 3) (x2+ 1) = 0
⇒ x + 3 = 0 of x2+1 = 0
⇒ x = -3, ±i
De gegeven vergelijking heeft dus een reële wortel, d.w.z. -3, en twee denkbeeldige wortels, d.w.z. ±i.
Probleem 4: Vind de wortels van vergelijking f(x) = x 3 – 7x 2 – x + 7 = 0.
Oplossing:
Gegeven uitdrukkingen,
f(x) = x3– 3x2– 5x + 7 = 0
Ontbind eerst de vergelijking f(x): x3– 3x2– 5x + 7= 0
Het kan worden omgezet in (x-7)(x+1)(x-1) = 0
Nadat we de polynoom in factoren hebben ontbonden, kunnen we de wortels vinden door elke factor gelijk te stellen aan nul. Bijvoorbeeld:
- x – 7 = 0, dus x = 7
- x + 1 = 0, dus x = -1
- x – 1 = 0, dus x = 1
Dus de wortels van de vergelijking f(x): x3– 3x2– 5x + 7 = 0 zijn
- x = 7
- x = -1
- x = 1
Probleem 5: Vind de wortels van vergelijking f(x) = x 3 − 6x 2 + 11x − 6 = 0, met behulp van de grafische methode.
Oplossing:
Gegeven uitdrukking: f(x) = x3− 6x2+ 11x − 6 = 0.
Vervang nu eenvoudig willekeurige waarden voor x in de grafiek voor de gegeven functie:
X
1
2
3
4
5
f(x)
0
0
0
6
24
We kunnen zien dat de grafiek de X-as op 3 punten heeft doorgesneden, dus er zijn 3 echte oplossingen.
Uit de grafiek zijn de oplossingen: x = 1, x = 2 en x = 3.
De wortels van de gegeven vergelijking zijn dus 1, 2 en 3.
voor lus in c
Oefenproblemen bij het oplossen van kubieke vergelijkingen
Hieronder zijn verschillende oefenproblemen met betrekking tot derdegraadsvergelijkingen toegevoegd. Los deze problemen op om het concept van Hoe de kubieke vergelijking op te lossen volledig te begrijpen?
P1. Los de derdegraadsvergelijking op, 3x3+ 2x2– 11x + 7 = 0.
P2. Vind de wortels van de derdegraadsvergelijking, 4x3– 12x2+ 17 = 0.
P3. Los de derdegraadsvergelijking x op3+ 4x2– x + 3 = 0 met behulp van een grafische methode.
P4. Zoek het getal dat voldoet, -9x3+ 11x2– 8x + 2 = 0.
Veelgestelde vragen over het oplossen van kubieke vergelijkingen
1. Wat zijn kubieke vergelijkingen?
Kubieke vergelijkingen zijn de algebraïsche vergelijkingen waarin de maximale macht van een variabele 3 is
2. Hoe ontbind je een kubieke vergelijking in factoren?
We kunnen een derdegraadsvergelijking op twee manieren ontbinden. Door eerst een lineaire uitdrukking te nemen die gebruikelijk is in de gegeven derdegraadsvergelijking, zullen we vervolgens een lineaire en een kwadratische uitdrukking als product hebben. Deze kwadratische vergelijking kan verder worden ontbonden om alle factoren te verkrijgen. De tweede methode is om een nulpunt van de gegeven derdegraadsvergelijking te vinden door willekeurige waarden in te voeren. De waarde waarvoor we de waarde van de vergelijking op nul krijgen, zal een van de nulpunten van de gegeven derdegraadsvergelijking zijn. Gebruik nu de factorstelling om een lineaire uitdrukking te vormen, laten we zeggen x-a en deel de gegeven derdegraadsvergelijking door deze uitdrukking, wat een kwadratische vergelijking als quotiënt oplevert. Deze verkregen kwadratische vergelijking kan verder worden ontbonden om alle factoren te verkrijgen.
3. Hoe los je een kubieke vergelijking grafisch op?
Om een derdegraadsvergelijking op te lossen, zet je willekeurige waarden voor x grafisch in de gegeven derdegraadsvergelijking en los je deze op, je krijgt de waarden van y. Zet deze verkregen waarden in de grafiek. Zoek de coördinaten waarop de grafiek de x-as snijdt. Deze coördinaten zijn de oplossing van de derdegraadsvergelijking.
4. Kunnen alle kubische vergelijkingen precies worden opgelost?
Elke vergelijking met een oneven macht moet één reële wortel hebben. Daarom moet een derdegraadsvergelijking ten minste één reële wortel hebben, in tegenstelling tot een kwadratische vergelijking waarbij beide wortels denkbeeldig kunnen zijn als de discriminant kleiner is dan nul.
5. Kan een derdegraadsvergelijking meerdere oplossingen hebben?
Ja, derdegraadsvergelijkingen kunnen meerdere oplossingen hebben, aangezien een derdegraadsvergelijking maximaal drie verschillende reële wortels kan hebben.
6. Wat bedoel je met de graad van een vergelijking?
Het maximale vermogen dat de variabele in een vergelijking bezit, wordt de graad van een polynoom genoemd.
7. Wat is het verschil tussen een polynoom en een vergelijking?
Polynoom is eenvoudigweg een algebraïsche vergelijking waarin de macht van de variabele een niet-negatief geheel getal is. Als dit polynoom wordt gelijkgesteld (=) met een numerieke waarde of een ander polynoom, wordt het een vergelijking genoemd.
8. Wat is de factorstelling voor derdegraadsvergelijkingen?
Factorstelling stelt dat als r een wortel (oplossing) is van de derdegraadsvergelijking ax3+ bx2+ cx + d = 0, dan is x – r een factor van de vergelijking.
9. Wat moet ik doen als ik geen exacte oplossingen kan vinden met behulp van formules?
Als het vinden van exacte oplossingen onmogelijk lijkt, kunnen we numerieke methoden zoals iteratieve methoden (bijvoorbeeld de methode van Newton) gebruiken om de wortels van de vergelijking te benaderen.
Leer meer over De methode van Newton Raphson .