 #practiceLinkDiv {weergave: geen! belangrijk; }
#practiceLinkDiv {weergave: geen! belangrijk; }Het Reverse Delete-algoritme is nauw verwant aan Het algoritme van Kruskal . In het algoritme van Kruskal is wat we doen: randen sorteren op toenemende volgorde van hun gewicht. Na het sorteren pakken we de randen één voor één in oplopende volgorde. We nemen de huidige gekozen rand op als we deze in de opspannende boom opnemen en er geen enkele cyclus ontstaat totdat er V-1-randen in de opspannende boom zijn waarbij V = aantal hoekpunten.
In het Reverse Delete-algoritme sorteren we alle randen afnemend volgorde van hun gewichten. Na het sorteren pakken we de randen één voor één in afnemende volgorde. Wij neem de huidige gekozen rand op als het uitsluiten van de huidige rand de verbinding in de huidige grafiek verbreekt . Het hoofdidee is het verwijderen van de rand als het verwijderen ervan niet leidt tot het ontkoppelen van de grafiek.
dereferentiewijzer
Het algoritme:
- Sorteer alle randen van de grafiek in niet-oplopende volgorde van randgewichten.
- Initialiseer MST als originele grafiek en verwijder extra randen met stap 3.
- Kies de hoogste gewichtsrand van de resterende randen en controleer of het verwijderen van de rand de verbinding met de grafiek verbreekt of niet .
Als de verbinding wordt verbroken, verwijderen we de rand niet.
Anders verwijderen we de rand en gaan verder.
Illustratie:
Laten we het begrijpen met het volgende voorbeeld:
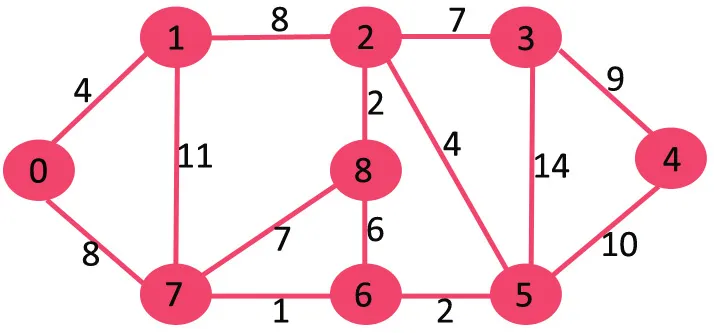
Als we de hoogste gewichtsrand van gewicht 14 verwijderen, wordt de grafiek niet losgekoppeld, dus verwijderen we deze.
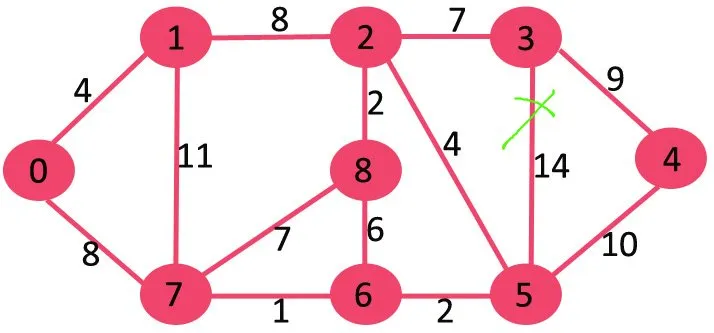
Vervolgens verwijderen we 11, omdat het verwijderen ervan de grafiek niet ontkoppelt.
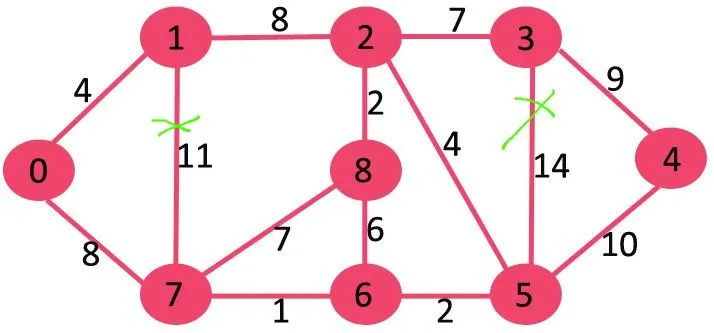
Vervolgens verwijderen we 10, omdat het verwijderen ervan de grafiek niet ontkoppelt.

Het volgende is 9. We kunnen 9 niet verwijderen, omdat het verwijderen ervan de verbinding verbreekt.

We gaan op deze manier verder en de volgende randen blijven in de uiteindelijke MST.
Edges in MST
(3 4)
(0 7)
(2 3)
(2 5)
(0 1)
(5 6)
(2 8)
(6 7)
Opmerking : In het geval van randen met hetzelfde gewicht kunnen we elke rand met randen met hetzelfde gewicht kiezen.
Aanbevolen praktijk Omgekeerd verwijderalgoritme voor minimaal overspannende boom Probeer het!Uitvoering:
C++// C++ program to find Minimum Spanning Tree // of a graph using Reverse Delete Algorithm #include
// Java program to find Minimum Spanning Tree // of a graph using Reverse Delete Algorithm import java.util.*; // class to represent an edge class Edge implements Comparable<Edge> { int u v w; Edge(int u int v int w) { this.u = u; this.w = w; this.v = v; } public int compareTo(Edge other) { return (this.w - other.w); } } // Class to represent a graph using adjacency list // representation public class GFG { private int V; // No. of vertices private List<Integer>[] adj; private List<Edge> edges; @SuppressWarnings({ 'unchecked' 'deprecated' }) public GFG(int v) // Constructor { V = v; adj = new ArrayList[v]; for (int i = 0; i < v; i++) adj[i] = new ArrayList<Integer>(); edges = new ArrayList<Edge>(); } // function to Add an edge public void AddEdge(int u int v int w) { adj[u].add(v); // Add w to v’s list. adj[v].add(u); // Add w to v’s list. edges.add(new Edge(u v w)); } // function to perform dfs private void DFS(int v boolean[] visited) { // Mark the current node as visited and print it visited[v] = true; // Recur for all the vertices adjacent to // this vertex for (int i : adj[v]) { if (!visited[i]) DFS(i visited); } } // Returns true if given graph is connected else false private boolean IsConnected() { boolean[] visited = new boolean[V]; // Find all reachable vertices from first vertex DFS(0 visited); // If set of reachable vertices includes all // return true. for (int i = 1; i < V; i++) { if (visited[i] == false) return false; } return true; } // This function assumes that edge (u v) // exists in graph or not public void ReverseDeleteMST() { // Sort edges in increasing order on basis of cost Collections.sort(edges); int mst_wt = 0; // Initialize weight of MST System.out.println('Edges in MST'); // Iterate through all sorted edges in // decreasing order of weights for (int i = edges.size() - 1; i >= 0; i--) { int u = edges.get(i).u; int v = edges.get(i).v; // Remove edge from undirected graph adj[u].remove(adj[u].indexOf(v)); adj[v].remove(adj[v].indexOf(u)); // Adding the edge back if removing it // causes disconnection. In this case this // edge becomes part of MST. if (IsConnected() == false) { adj[u].add(v); adj[v].add(u); // This edge is part of MST System.out.println('(' + u + ' ' + v + ')'); mst_wt += edges.get(i).w; } } System.out.println('Total weight of MST is ' + mst_wt); } // Driver code public static void main(String[] args) { // create the graph given in above figure int V = 9; GFG g = new GFG(V); // making above shown graph g.AddEdge(0 1 4); g.AddEdge(0 7 8); g.AddEdge(1 2 8); g.AddEdge(1 7 11); g.AddEdge(2 3 7); g.AddEdge(2 8 2); g.AddEdge(2 5 4); g.AddEdge(3 4 9); g.AddEdge(3 5 14); g.AddEdge(4 5 10); g.AddEdge(5 6 2); g.AddEdge(6 7 1); g.AddEdge(6 8 6); g.AddEdge(7 8 7); g.ReverseDeleteMST(); } } // This code is contributed by Prithi_Dey
# Python3 program to find Minimum Spanning Tree # of a graph using Reverse Delete Algorithm # Graph class represents a directed graph # using adjacency list representation class Graph: def __init__(self v): # No. of vertices self.v = v self.adj = [0] * v self.edges = [] for i in range(v): self.adj[i] = [] # function to add an edge to graph def addEdge(self u: int v: int w: int): self.adj[u].append(v) # Add w to v’s list. self.adj[v].append(u) # Add w to v’s list. self.edges.append((w (u v))) def dfs(self v: int visited: list): # Mark the current node as visited and print it visited[v] = True # Recur for all the vertices adjacent to # this vertex for i in self.adj[v]: if not visited[i]: self.dfs(i visited) # Returns true if graph is connected # Returns true if given graph is connected else false def connected(self): visited = [False] * self.v # Find all reachable vertices from first vertex self.dfs(0 visited) # If set of reachable vertices includes all # return true. for i in range(1 self.v): if not visited[i]: return False return True # This function assumes that edge (u v) # exists in graph or not def reverseDeleteMST(self): # Sort edges in increasing order on basis of cost self.edges.sort(key = lambda a: a[0]) mst_wt = 0 # Initialize weight of MST print('Edges in MST') # Iterate through all sorted edges in # decreasing order of weights for i in range(len(self.edges) - 1 -1 -1): u = self.edges[i][1][0] v = self.edges[i][1][1] # Remove edge from undirected graph self.adj[u].remove(v) self.adj[v].remove(u) # Adding the edge back if removing it # causes disconnection. In this case this # edge becomes part of MST. if self.connected() == False: self.adj[u].append(v) self.adj[v].append(u) # This edge is part of MST print('( %d %d )' % (u v)) mst_wt += self.edges[i][0] print('Total weight of MST is' mst_wt) # Driver Code if __name__ == '__main__': # create the graph given in above figure V = 9 g = Graph(V) # making above shown graph g.addEdge(0 1 4) g.addEdge(0 7 8) g.addEdge(1 2 8) g.addEdge(1 7 11) g.addEdge(2 3 7) g.addEdge(2 8 2) g.addEdge(2 5 4) g.addEdge(3 4 9) g.addEdge(3 5 14) g.addEdge(4 5 10) g.addEdge(5 6 2) g.addEdge(6 7 1) g.addEdge(6 8 6) g.addEdge(7 8 7) g.reverseDeleteMST() # This code is contributed by # sanjeev2552
// C# program to find Minimum Spanning Tree // of a graph using Reverse Delete Algorithm using System; using System.Collections.Generic; // class to represent an edge public class Edge : IComparable<Edge> { public int u v w; public Edge(int u int v int w) { this.u = u; this.v = v; this.w = w; } public int CompareTo(Edge other) { return this.w.CompareTo(other.w); } } // Graph class represents a directed graph // using adjacency list representation public class Graph { private int V; // No. of vertices private List<int>[] adj; private List<Edge> edges; public Graph(int v) // Constructor { V = v; adj = new List<int>[ v ]; for (int i = 0; i < v; i++) adj[i] = new List<int>(); edges = new List<Edge>(); } // function to Add an edge public void AddEdge(int u int v int w) { adj[u].Add(v); // Add w to v’s list. adj[v].Add(u); // Add w to v’s list. edges.Add(new Edge(u v w)); } // function to perform dfs private void DFS(int v bool[] visited) { // Mark the current node as visited and print it visited[v] = true; // Recur for all the vertices adjacent to // this vertex foreach(int i in adj[v]) { if (!visited[i]) DFS(i visited); } } // Returns true if given graph is connected else false private bool IsConnected() { bool[] visited = new bool[V]; // Find all reachable vertices from first vertex DFS(0 visited); // If set of reachable vertices includes all // return true. for (int i = 1; i < V; i++) { if (visited[i] == false) return false; } return true; } // This function assumes that edge (u v) // exists in graph or not public void ReverseDeleteMST() { // Sort edges in increasing order on basis of cost edges.Sort(); int mst_wt = 0; // Initialize weight of MST Console.WriteLine('Edges in MST'); // Iterate through all sorted edges in // decreasing order of weights for (int i = edges.Count - 1; i >= 0; i--) { int u = edges[i].u; int v = edges[i].v; // Remove edge from undirected graph adj[u].Remove(v); adj[v].Remove(u); // Adding the edge back if removing it // causes disconnection. In this case this // edge becomes part of MST. if (IsConnected() == false) { adj[u].Add(v); adj[v].Add(u); // This edge is part of MST Console.WriteLine('({0} {1})' u v); mst_wt += edges[i].w; } } Console.WriteLine('Total weight of MST is {0}' mst_wt); } } class GFG { // Driver code static void Main(string[] args) { // create the graph given in above figure int V = 9; Graph g = new Graph(V); // making above shown graph g.AddEdge(0 1 4); g.AddEdge(0 7 8); g.AddEdge(1 2 8); g.AddEdge(1 7 11); g.AddEdge(2 3 7); g.AddEdge(2 8 2); g.AddEdge(2 5 4); g.AddEdge(3 4 9); g.AddEdge(3 5 14); g.AddEdge(4 5 10); g.AddEdge(5 6 2); g.AddEdge(6 7 1); g.AddEdge(6 8 6); g.AddEdge(7 8 7); g.ReverseDeleteMST(); } } // This code is contributed by cavi4762
// Javascript program to find Minimum Spanning Tree // of a graph using Reverse Delete Algorithm // Graph class represents a directed graph // using adjacency list representation class Graph { // Constructor constructor(V) { this.V = V; this.adj = []; this.edges = []; for (let i = 0; i < V; i++) { this.adj[i] = []; } } // function to add an edge to graph addEdge(u v w) { this.adj[u].push(v);// Add w to v’s list. this.adj[v].push(u);// Add w to v’s list. this.edges.push([w [u v]]); } DFS(v visited) { // Mark the current node as visited and print it visited[v] = true; for (const i of this.adj[v]) { if (!visited[i]) { this.DFS(i visited); } } } // Returns true if given graph is connected else false isConnected() { const visited = []; for (let i = 0; i < this.V; i++) { visited[i] = false; } // Find all reachable vertices from first vertex this.DFS(0 visited); // If set of reachable vertices includes all // return true. for (let i = 1; i < this.V; i++) { if (!visited[i]) { return false; } } return true; } // This function assumes that edge (u v) // exists in graph or not reverseDeleteMST() { // Sort edges in increasing order on basis of cost this.edges.sort((a b) => a[0] - b[0]); let mstWt = 0;// Initialize weight of MST console.log('Edges in MST'); // Iterate through all sorted edges in // decreasing order of weights for (let i = this.edges.length - 1; i >= 0; i--) { const [u v] = this.edges[i][1]; // Remove edge from undirected graph this.adj[u] = this.adj[u].filter(x => x !== v); this.adj[v] = this.adj[v].filter(x => x !== u); // Adding the edge back if removing it // causes disconnection. In this case this // edge becomes part of MST. if (!this.isConnected()) { this.adj[u].push(v); this.adj[v].push(u); // This edge is part of MST console.log(`(${u} ${v})`); mstWt += this.edges[i][0]; } } console.log(`Total weight of MST is ${mstWt}`); } } // Driver code function main() { // create the graph given in above figure var V = 9; var g = new Graph(V); // making above shown graph g.addEdge(0 1 4); g.addEdge(0 7 8); g.addEdge(1 2 8); g.addEdge(1 7 11); g.addEdge(2 3 7); g.addEdge(2 8 2); g.addEdge(2 5 4); g.addEdge(3 4 9); g.addEdge(3 5 14); g.addEdge(4 5 10); g.addEdge(5 6 2); g.addEdge(6 7 1); g.addEdge(6 8 6); g.addEdge(7 8 7); g.reverseDeleteMST(); } main();
Uitvoer
Edges in MST (3 4) (0 7) (2 3) (2 5) (0 1) (5 6) (2 8) (6 7) Total weight of MST is 37
Tijdcomplexiteit: O((E*(V+E)) + E log E) waarbij E het aantal randen is.
Ruimtecomplexiteit: O(V+E) waarbij V het aantal hoekpunten is en E het aantal randen. We gebruiken de aangrenzende lijst om de grafiek op te slaan, dus we hebben een ruimte nodig die evenredig is met O(V+E).
Opmerkingen:
verbinding java-mysql
- De bovenstaande implementatie is een eenvoudige/naïeve implementatie van het Reverse Delete-algoritme en kan worden geoptimaliseerd tot O(E log V (log log V)3) [Bron : Een week ]. Maar deze geoptimaliseerde tijdscomplexiteit is nog steeds minder dan Prim En Kruskal Algoritmen voor MST.
- De bovenstaande implementatie wijzigt de originele grafiek. We kunnen een kopie van de grafiek maken als de originele grafiek behouden moet blijven.
Quiz maken
