Een recursieve functie kan worden gedefinieerd als een routine die zichzelf direct of indirect aanroept.
Met andere woorden, een recursieve functie is een functie die een probleem oplost door kleinere exemplaren van hetzelfde probleem op te lossen. Deze techniek wordt vaak gebruikt bij het programmeren om problemen op te lossen die kunnen worden opgesplitst in eenvoudigere, vergelijkbare subproblemen.
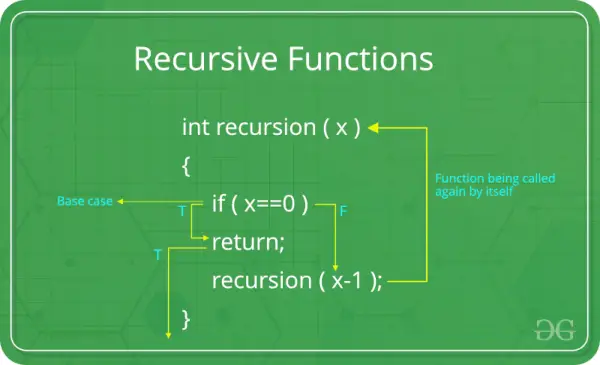
Behoefte aan recursieve functie:
Een recursieve functie is een functie die een probleem oplost door kleinere exemplaren van hetzelfde probleem op te lossen. Deze techniek wordt vaak gebruikt bij het programmeren om problemen op te lossen die kunnen worden opgesplitst in eenvoudigere, vergelijkbare subproblemen.
1. Complexe taken oplossen:
Recursieve functies splitsen complexe problemen op in kleinere exemplaren van hetzelfde probleem, wat resulteert in compacte en leesbare code.
2. Verdeel en heers:
Recursieve functies zijn geschikt voor verdeel-en-heers-algoritmen zoals merge sort en quicksort, waarbij problemen in kleinere subproblemen worden opgedeeld, deze recursief worden opgelost en de oplossingen worden samengevoegd met het oorspronkelijke probleem.
3. Terugkeren :
Recursieve backtracking is ideaal voor het verkennen en oplossen van problemen zoals N-Queens en Sudoku.
4. Dynamisch programmering:
Recursieve functies lossen dynamische programmeerproblemen efficiënt op door deelproblemen op te lossen en hun oplossingen te combineren tot een complete oplossing.
5. Boom en grafiekstructuren:
Recursieve functies zijn ideaal voor het werken met boom- en grafiekstructuren, waardoor verplaatsings- en patroonherkenningstaken worden vereenvoudigd .
Hoe schrijf je een recursieve functie:
Componenten van een recursieve functie:
Hoofdzaak: Elke recursieve functie moet een basisscenario hebben. Het basisscenario is het eenvoudigste scenario waarvoor geen verdere recursie vereist is. Dit is een beëindigingsvoorwaarde die voorkomt dat de functie zichzelf voor onbepaalde tijd kan aanroepen. Zonder een goed basisscenario kan een recursieve functie tot oneindige recursie leiden.
Recursief geval: In het recursieve geval roept de functie zichzelf aan met de gewijzigde argumenten. Dit is de essentie van recursie: een groter probleem oplossen door het op te splitsen in kleinere exemplaren van hetzelfde probleem. Het recursieve geval moet bij elke iteratie dichter bij het basisscenario komen.
Laten we eens kijken naar het voorbeeld van faculteit van getal :
hrithik roshan
In dit voorbeeld is het basisscenario wanneer N is 0 , en de functie retourneert 1 . Het recursieve geval vermenigvuldigt zich N met het resultaat van de functie die met parameter wordt aangeroepen n – 1 . Het proces gaat door totdat het basisscenario is bereikt.
Het is essentieel om ervoor te zorgen dat de recursieve functie een correct basisscenario heeft en dat de recursieve aanroepen naar het basisscenario leiden, anders kan de procedure voor onbepaalde tijd worden uitgevoerd, wat leidt tot een stackoverflow (waarbij het beschikbare geheugen wordt overschreden dat is toegewezen voor functieaanroepen).
Hieronder vindt u de implementatie van faculteit van een getal:
C++ #include using namespace std; // Recursive Function to calculate Factorial of a number int factorial(int n) { // Base case if (n == 0) { return 1; } // Recursive case return n * factorial(n - 1); } // Driver Code int main() { int n = 4; cout << 'Factorial of ' << n << ' is:' << factorial(n); return 0; }> Java import java.util.Scanner; public class Factorial { // Recursive Function to calculate the factorial of a number static int factorial(int n) { // Base case: If n is 0, the factorial is 1. if (n == 0) { return 1; } // Recursive case: Calculate the factorial by multiplying n with the factorial of (n - 1). return n * factorial(n - 1); } public static void main(String[] args) { int n = 4; // Calculate and print the factorial of n. int result = factorial(n); System.out.println('Factorial of ' + n + ' is: ' + result); } }> Python # Recursive Function to calculate Factorial of a number def factorial(n): # Base case if n == 0: return 1 # Recursive case return n * factorial(n - 1) # Driver Code if __name__ == '__main__': n = 4 print('Factorial of', n, 'is:', factorial(n))> C# using System; class Program { // Recursive Function to calculate Factorial of a number static int Factorial(int n) { // Base case if (n == 0) { return 1; } // Recursive case return n * Factorial(n - 1); } // Driver Code static void Main() { int n = 4; Console.WriteLine('Factorial of ' + n + ' is: ' + Factorial(n)); } }> Javascript // Function to calculate the factorial of a number using recursion function factorial(n) { // Base case: If n is 0, the factorial is 1. if (n === 0) { return 1; } // Recursive case: Calculate the factorial by multiplying n with the factorial of (n - 1). return n * factorial(n - 1); } // Main function function main() { // Given number let n = 4; // Calculate the factorial of n. let result = factorial(n); // Print the result console.log('Factorial of ' + n + ' is: ' + result); } // Call the main function main();> Uitvoer
Factorial of 4 is:24>
Tijdcomplexiteit: Op)
Hulpruimte: Op)
