A Gegevensstructuur van wachtrij is een fundamenteel concept in de computerwetenschappen dat wordt gebruikt voor het opslaan en beheren van gegevens in een specifieke volgorde. Het volgt het principe van Als eerste erin, als eerste eruit (FIFO) , waarbij het eerste element dat aan de wachtrij wordt toegevoegd, het eerste is dat wordt verwijderd. Wachtrijen worden vaak gebruikt in verschillende algoritmen en toepassingen vanwege hun eenvoud en efficiëntie bij het beheren van de gegevensstroom.

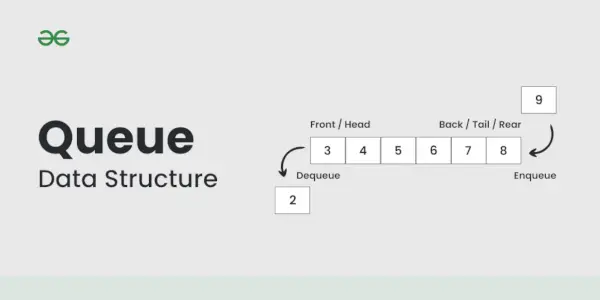
Gegevensstructuur van wachtrij

Inhoudsopgave

• Toepassingen van wachtrij
• Implementaties van Queue in verschillende programmeertalen
• Wat is wachtrij in gegevensstructuren?

  Een wachtrij is een lineaire gegevensstructuur die volgt op de First-In-First-Out (FIFO) beginsel. Het werkt als een lijn waarbij aan één uiteinde elementen worden toegevoegd ( achterkant ) en verwijderd van het andere uiteinde ( voorkant ).

  Wachtrij verwijderen (verwijderen) : Verwijdert het element van de voorkant van de wachtrij en retourneert het.

• Kijkje : Retourneert het element vooraan in de wachtrij zonder het te verwijderen.
• Leeg : Controleert of de wachtrij leeg is.
• Vol : Controleert of de wachtrij vol is.

• Wachtrij in C++ Standard Template Library (STL)
• Wachtrijinterface in Java
• Wachtrij in Python
• Wachtrij in C#
• Wachtrij in Javascript

Implementeer een stapel met behulp van één wachtrij

Implementeer wachtrij met behulp van stapels

Hoe k-wachtrijen efficiënt in een enkele array implementeren?

LRU-cache-implementatie

Detecteer cyclus in een ongerichte grafiek met behulp van BFS

Breedte eerst zoeken of BFS voor een grafiek

Directory doorkruisen in Java met behulp van BFS

Verticale orderdoorgang van binaire boom met behulp van Map

Afdrukken Rechteraanzicht van een binaire boom

Vind de minimale diepte van een binaire boom

Controleer of een bepaalde grafiek bipartiet is of niet

Niveau met maximaal aantal knooppunten

Zoek of er een pad is tussen twee hoekpunten in een gerichte graaf

Druk alle knooppunten tussen twee gegeven niveaus in de binaire boom af

Zoek het volgende rechterknooppunt van een bepaalde sleutel

Minimale stappen om het doel van een ridder te bereiken

Eilanden in een grafiek met behulp van BFS

Niveauorder regel voor regel doorlopen | Set 3 (met één wachtrij)

Zoek het eerste niet-herhalende karakter uit een stroom karakters

Algoritme voor overstroming

Minimale tijd die nodig is om alle sinaasappels te laten rotten

Kortste pad in een binair doolhof

Een interessante methode om binaire getallen van 1 tot n te genereren

Maximaal kostenpad van bronknooppunt naar bestemming

Kortste afstand tussen twee cellen in een matrix of raster

Slang- en ladderprobleem

Vind de kortste veilige route op een pad met landmijnen

Tel alle mogelijke wandelingen van een bron naar een bestemming met precies K-randen

Minimale kosten van eenvoudig pad tussen twee knooppunten in een gerichte en gewogen grafiek

Minimumkostenpad in een gerichte grafiek via een gegeven reeks tussenliggende knooppunten

Vind de eerste rondrit die alle benzinepompen bezoekt

Snelle links:

• ‘Video’s’ in wachtrij
• Aanbevolen:
  • Leer datastructuur en algoritmen | DSA-zelfstudie
  • Wachtrij in Go-taal
  • Wachtrij in Scala