De kwantiel-kwantielplot (q-q plot) is een grafische methode om te bepalen of een dataset een bepaalde waarschijnlijkheidsverdeling volgt of dat twee gegevensmonsters afkomstig zijn van dezelfde bevolking of niet. Q-Q-plots zijn vooral nuttig om te beoordelen of een dataset dat wel is normaal verdeeld of als het een andere bekende verdeling volgt. Ze worden vaak gebruikt in statistieken, data-analyse en kwaliteitscontrole om aannames te controleren en afwijkingen van verwachte verdelingen te identificeren.
Kwantielen en percentielen
Kwantielen zijn punten in een dataset die de gegevens verdelen in intervallen die gelijke kansen of proporties van de totale verdeling bevatten. Ze worden vaak gebruikt om de verspreiding of distributie van een dataset te beschrijven. De meest voorkomende kwantielen zijn:
- Mediaan (50e percentiel) : De mediaan is de middelste waarde van een gegevensset wanneer deze is gerangschikt van klein naar groot. Het verdeelt de dataset in twee gelijke helften.
- Kwartielen (25e, 50e en 75e percentiel) : Kwartielen verdelen de dataset in vier gelijke delen. Het eerste kwartiel (Q1) is de waarde waaronder 25% van de gegevens valt, het tweede kwartiel (Q2) is de mediaan en het derde kwartiel (Q3) is de waarde waaronder 75% van de gegevens valt.
- Percentielen : Percentielen zijn vergelijkbaar met kwartielen, maar verdelen de dataset in 100 gelijke delen. Het 90e percentiel is bijvoorbeeld de waarde waaronder 90% van de gegevens valt.
Opmerking:
- Een q-q-plot is een grafiek van de kwantielen van de eerste dataset tegen de kwantielen van de tweede dataset.
- Ter referentie wordt ook een 45%-lijn uitgezet; Voor als de monsters uit dezelfde populatie komen, liggen de punten langs deze lijn.
Normale verdeling:
De normale verdeling (ook wel Gaussiaanse verdeling Bell-curve genoemd) is een continue waarschijnlijkheidsverdeling die de verdeling vertegenwoordigt die is verkregen uit de willekeurig gegenereerde reële waarden.
. 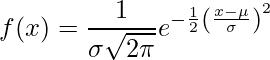

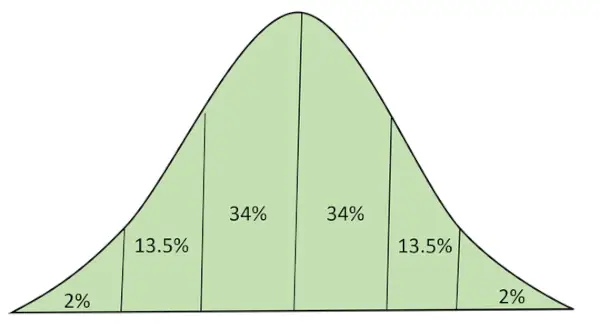
Normale verdeling met oppervlakte onder curve
Hoe Q-Q-plot tekenen?
Om een Quantile-Quantile (Q-Q)-plot te tekenen, kunt u deze stappen volgen:
- Verzamel de gegevens : Verzamel de gegevensset waarvoor u de Q-Q-plot wilt maken. Zorg ervoor dat de gegevens numeriek zijn en een willekeurige steekproef uit de populatie van interesse vertegenwoordigen.
- Sorteer de gegevens : Rangschik de gegevens in oplopende of aflopende volgorde. Deze stap is essentieel voor het nauwkeurig berekenen van kwantielen.
- Kies een theoretische verdeling : Bepaal de theoretische verdeling waarmee u uw dataset wilt vergelijken. Veelvoorkomende keuzes zijn onder meer de normale verdeling, de exponentiële verdeling of een andere verdeling die goed bij uw gegevens past.
- Bereken theoretische kwantielen : Bereken de kwantielen voor de gekozen theoretische verdeling. Als u bijvoorbeeld vergelijkt met een normale verdeling, gebruikt u de inverse cumulatieve verdelingsfunctie (CDF) van de normale verdeling om de verwachte kwantielen te vinden.
- Plotten :
- Zet de gesorteerde gegevenssetwaarden op de x-as.
- Zet de overeenkomstige theoretische kwantielen op de y-as.
- Elk gegevenspunt (x, y) vertegenwoordigt een paar waargenomen en verwachte waarden.
- Verbind de datapunten om de relatie tussen de dataset en de theoretische distributie visueel te inspecteren.
Interpretatie van Q-Q-plot
- Als de punten op de grafiek ongeveer langs een rechte lijn liggen, betekent dit dat uw dataset de veronderstelde verdeling volgt.
- Afwijkingen van de rechte lijn duiden op afwijkingen van de veronderstelde verdeling, die verder onderzoek vereisen.
Onderzoek naar de gelijkenis van distributie met Q-Q-plots
Het onderzoeken van distributieovereenkomst met behulp van Q-Q-plots is een fundamentele taak in de statistiek. Het vergelijken van twee datasets om te bepalen of ze afkomstig zijn uit dezelfde distributie is van cruciaal belang voor verschillende analytische doeleinden. Wanneer de aanname van een gemeenschappelijke distributie geldt, kan het samenvoegen van datasets de nauwkeurigheid van parameterschattingen verbeteren, bijvoorbeeld voor locatie en schaal. Q-Q-plots, een afkorting van kwantiel-kwantielplots, bieden een visuele methode voor het beoordelen van de gelijkenis van de distributie. In deze grafieken worden kwantielen uit de ene dataset uitgezet tegen kwantielen uit een andere dataset. Als de punten nauw op één lijn liggen langs een diagonale lijn, suggereert dit gelijkenis tussen de verdelingen. Afwijkingen van deze diagonale lijn duiden op verschillen in distributiekarakteristieken.
Terwijl tests zoals de chi-kwadraat En Kolmogorov-Smirnov tests kunnen algemene distributieverschillen evalueren, Q-Q-plots bieden een genuanceerd perspectief door kwantielen rechtstreeks te vergelijken. Hierdoor kunnen analisten specifieke verschillen onderscheiden, zoals verschuivingen in locatie of schaalveranderingen, die mogelijk niet duidelijk uit formele statistische tests alleen blijken.
Python-implementatie van Q-Q-plot
Python3
import> numpy as np> import> matplotlib.pyplot as plt> import> scipy.stats as stats> # Generate example data> np.random.seed(>0>)> data>=> np.random.normal(loc>=>0>, scale>=>1>, size>=>1000>)> # Create Q-Q plot> stats.probplot(data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Normal Q-Q plot'>)> plt.xlabel(>'Theoretical quantiles'>)> plt.ylabel(>'Ordered Values'>)> plt.grid(>True>)> plt.show()> |
>
>
Uitgang:
Q-Q-plot
Omdat de gegevenspunten hier ongeveer een rechte lijn volgen in de Q-Q-grafiek, suggereert dit dat de gegevensset consistent is met de veronderstelde theoretische verdeling, waarvan we in dit geval aannamen dat deze de normale verdeling was.
Voordelen van Q-Q-plot
- Flexibele vergelijking : Q-Q-plots kunnen datasets van verschillende groottes vergelijken zonder gelijke steekproefomvang vereisen.
- Dimensieloze analyse : Ze zijn dimensieloos, waardoor ze geschikt zijn om datasets mee te vergelijken verschillende eenheden of schalen.
- Visuele interpretatie : Biedt een duidelijke visuele weergave van de gegevensdistributie in vergelijking met een theoretische distributie.
- Gevoelig voor afwijkingen : Detecteert gemakkelijk afwijkingen van veronderstelde verdelingen, wat helpt bij het identificeren van gegevensverschillen.
- Diagnostisch hulpmiddel : Helpt bij het beoordelen van verdelingsaannames, het identificeren van uitschieters en het begrijpen van gegevenspatronen.
Toepassingen van kwantiel-kwantielplot
De Quantile-Quantile-plot wordt gebruikt voor het volgende doel:
- Verdelingsveronderstellingen beoordelen : Q-Q-plots worden vaak gebruikt om visueel te inspecteren of een dataset een specifieke waarschijnlijkheidsverdeling volgt, zoals de normale verdeling. Door de kwantielen van de waargenomen gegevens te vergelijken met de kwantielen van de veronderstelde verdeling kunnen afwijkingen van de veronderstelde verdeling worden gedetecteerd. Dit is cruciaal in veel statistische analyses, waarbij de geldigheid van verdelingsaannames de nauwkeurigheid van statistische gevolgtrekkingen beïnvloedt.
- Uitschieters detecteren : Uitschieters zijn gegevenspunten die aanzienlijk afwijken van de rest van de gegevensset. Q-Q-plots kunnen helpen bij het identificeren van uitschieters door gegevenspunten te onthullen die ver afwijken van het verwachte patroon van de verdeling. Uitschieters kunnen verschijnen als punten die afwijken van de verwachte rechte lijn in de grafiek.
- Uitkeringen vergelijken : Q-Q-plots kunnen worden gebruikt om twee datasets te vergelijken om te zien of ze uit dezelfde distributie komen. Dit wordt bereikt door de kwantielen van de ene dataset uit te zetten tegen de kwantielen van een andere dataset. Als de punten ongeveer langs een rechte lijn vallen, suggereert dit dat de twee datasets uit dezelfde verdeling komen.
- Normaliteit beoordelen : Q-Q-plots zijn bijzonder nuttig voor het beoordelen van de normaliteit van een dataset. Als de gegevenspunten in de grafiek nauwgezet een rechte lijn volgen, geeft dit aan dat de gegevensset ongeveer normaal verdeeld is. Afwijkingen van de lijn duiden op afwijkingen van de normaliteit, waarvoor mogelijk verder onderzoek of niet-parametrische statistische technieken nodig zijn.
- Modelvalidatie : Op gebieden als econometrie en machinaal leren worden Q-Q-plots gebruikt om voorspellende modellen te valideren. Door de kwantielen van waargenomen reacties te vergelijken met de kwantielen die door een model worden voorspeld, kan men beoordelen hoe goed het model bij de gegevens past. Afwijkingen van het verwachte patroon kunnen wijzen op gebieden waar het model verbetering behoeft.
- Kwaliteitscontrole : Q-Q-plots worden gebruikt in kwaliteitscontroleprocessen om de verdeling van gemeten of waargenomen waarden in de loop van de tijd of over verschillende batches te monitoren. Afwijkingen van verwachte patronen in de plot kunnen veranderingen in de onderliggende processen signaleren, wat aanleiding geeft tot verder onderzoek.
Soorten Q-Q-plots
Er zijn verschillende soorten Q-Q-plots die vaak worden gebruikt in statistieken en data-analyse, elk geschikt voor verschillende scenario's of doeleinden:
- Normale verdeling : Een symmetrische verdeling waarbij de Q-Q-grafiek punten ongeveer langs een diagonale lijn zou tonen als de gegevens een normale verdeling volgen.
- Rechtsscheve verdeling : Een verdeling waarbij de Q-Q-grafiek een patroon vertoont waarbij de waargenomen kwantielen afwijken van de rechte lijn naar het bovenste uiteinde, wat wijst op een langere staart aan de rechterkant.
- Linksscheve verdeling : Een verdeling waarbij de Q-Q-grafiek een patroon vertoont waarbij de waargenomen kwantielen afwijken van de rechte lijn naar het onderste uiteinde, wat wijst op een langere staart aan de linkerkant.
- Onderverspreide distributie : Een verdeling waarbij de Q-Q-plot waargenomen kwantielen strakker rond de diagonale lijn zou laten zien in vergelijking met de theoretische kwantielen, wat een lagere variantie suggereert.
- Oververspreide distributie : Een verdeling waarbij de Q-Q-grafiek waargenomen kwantielen weergeeft die meer verspreid zijn of afwijken van de diagonale lijn, wat wijst op een grotere variantie of spreiding vergeleken met de theoretische verdeling.
Python3
import> numpy as np> import> matplotlib.pyplot as plt> import> scipy.stats as stats> # Generate a random sample from a normal distribution> normal_data>=> np.random.normal(loc>=>0>, scale>=>1>, size>=>1000>)> # Generate a random sample from a right-skewed distribution (exponential distribution)> right_skewed_data>=> np.random.exponential(scale>=>1>, size>=>1000>)> # Generate a random sample from a left-skewed distribution (negative exponential distribution)> left_skewed_data>=> ->np.random.exponential(scale>=>1>, size>=>1000>)> # Generate a random sample from an under-dispersed distribution (truncated normal distribution)> under_dispersed_data>=> np.random.normal(loc>=>0>, scale>=>0.5>, size>=>1000>)> under_dispersed_data>=> under_dispersed_data[(under_dispersed_data>>->1>) & (under_dispersed_data <>1>)]># Truncate> # Generate a random sample from an over-dispersed distribution (mixture of normals)> over_dispersed_data>=> np.concatenate((np.random.normal(loc>=>->2>, scale>=>1>, size>=>500>),> >np.random.normal(loc>=>2>, scale>=>1>, size>=>500>)))> # Create Q-Q plots> plt.figure(figsize>=>(>15>,>10>))> plt.subplot(>2>,>3>,>1>)> stats.probplot(normal_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Normal Distribution'>)> plt.subplot(>2>,>3>,>2>)> stats.probplot(right_skewed_data, dist>=>'expon'>, plot>=>plt)> plt.title(>'Q-Q Plot - Right-skewed Distribution'>)> plt.subplot(>2>,>3>,>3>)> stats.probplot(left_skewed_data, dist>=>'expon'>, plot>=>plt)> plt.title(>'Q-Q Plot - Left-skewed Distribution'>)> plt.subplot(>2>,>3>,>4>)> stats.probplot(under_dispersed_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Under-dispersed Distribution'>)> plt.subplot(>2>,>3>,>5>)> stats.probplot(over_dispersed_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Over-dispersed Distribution'>)> plt.tight_layout()> plt.show()> |
>
>
Uitgang:
Q-Q-plot voor verschillende distributies
arraylijst
