• Pushdown-automaten zijn een manier om een ​​CFG te implementeren op dezelfde manier waarop we DFA ontwerpen voor een reguliere grammatica. Een DFA kan een eindige hoeveelheid informatie onthouden, maar een PDA kan een oneindige hoeveelheid informatie onthouden.
• Pushdown-automaten zijn eenvoudigweg een NFA aangevuld met een 'extern stapelgeheugen'. De toevoeging van een stapel wordt gebruikt om Pushdown-automaten een last-in-first-out-geheugenbeheermogelijkheid te bieden. Pushdown-automaten kunnen een onbeperkte hoeveelheid informatie op de stapel opslaan. Het heeft toegang tot een beperkte hoeveelheid informatie op de stapel. Een PDA kan een element op de bovenkant van de stapel duwen en er een element vanaf de bovenkant van de stapel afhalen. Om een ​​element in de stapel te lezen, moeten de bovenste elementen worden verwijderd en gaan ze verloren.
• Een PDA is krachtiger dan FA. Elke taal die aanvaardbaar kan zijn voor FA, kan ook aanvaardbaar zijn voor PDA. PDA accepteert ook een taalklasse die zelfs niet door FA kan worden geaccepteerd. PDA is dus veel superieur aan FA.

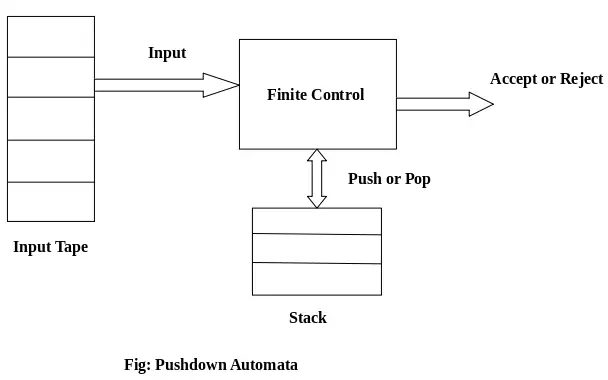
PDA-componenten:

Invoerband: De invoerband is verdeeld in vele cellen of symbolen. De invoerkop is alleen-lezen en mag slechts één symbool tegelijk van links naar rechts bewegen.

Eindige controle: De eindige controle heeft een aanwijzer die naar het huidige symbool wijst dat moet worden gelezen.

Stapel: De stapel is een structuur waarin we de items slechts aan één kant kunnen duwen en verwijderen. Het heeft een oneindige omvang. Bij PDA wordt de stapel gebruikt om de items tijdelijk op te slaan.

Formele definitie van PDA:

De PDA kan worden gedefinieerd als een verzameling van 7 componenten:

Q: de eindige reeks toestanden

∑: de invoer ingesteld

C: een stapelsymbool dat van de stapel kan worden geduwd en gepoft

Q0: de initiële staat

roep een js-functie aan vanuit html

MET: een startsymbool dat in Γ staat.

F: een reeks eindtoestanden

D: mapping-functie die wordt gebruikt om van de huidige staat naar de volgende staat te gaan.

Onmiddellijke beschrijving (ID)

ID is een informele notatie van hoe een PDA een invoerreeks berekent en beslist of de reeks wordt geaccepteerd of afgewezen.

Een onmiddellijke beschrijving is een drievoudige (q, w, α) waarbij:

Q beschrijft de huidige staat.

In beschrijft de resterende invoer.

dhanashree verma

A beschrijft de stapelinhoud, linksboven.

Tourniquet-notatie:

⊢ teken beschrijft de tourniquetnotatie en vertegenwoordigt één beweging.

⊢* teken beschrijft een reeks zetten.

Bijvoorbeeld,

(p, b, T) ⊢ (q, w, α)

Java instellen

In het bovenstaande voorbeeld wordt bij een overgang van toestand p naar q het invoersymbool 'b' verbruikt en wordt de bovenkant van de stapel 'T' weergegeven door een nieuwe string α.

Voorbeeld 1:

Ontwerp een PDA voor het accepteren van een taal a^NB²ⁿ.

Oplossing: In deze taal moet n aantal a's gevolgd worden door 2n aantal b's. Daarom zullen we een heel eenvoudige logica toepassen, en dat betekent dat als we één 'a' lezen, we twee a's op de stapel zullen duwen. Zodra we 'b' lezen, zou voor elke afzonderlijke 'b' slechts één 'a' van de stapel moeten worden geplukt.

De ID kan als volgt worden opgebouwd:

 δ(q0, a, Z) = (q0, aaZ) δ(q0, a, a) = (q0, aaa) 

Als we nu b lezen, veranderen we de status van q0 in q1 en beginnen we de corresponderende 'a' te laten verschijnen. Vandaar,

 δ(q0, b, a) = (q1, ε) 

Dit proces van het laten verschijnen van 'b' zal dus worden herhaald, tenzij alle symbolen worden gelezen. Merk op dat de popping-actie alleen plaatsvindt in toestand q1.

 δ(q1, b, a) = (q1, ε) 

Na het lezen van alle b's zouden alle corresponderende a's moeten verschijnen. Als we dus ε als invoersymbool lezen, zou er niets in de stapel moeten staan. De verhuizing zal dus zijn:

 δ(q1, ε, Z) = (q2, ε) 

Waar

PDA = ({q0, q1, q2}, {a, b}, {a, Z}, δ, q0, Z, {q2})

We kunnen de ID samenvatten als:

 δ(q0, a, Z) = (q0, aaZ) δ(q0, a, a) = (q0, aaa) δ(q0, b, a) = (q1, ε) δ(q1, b, a) = (q1, ε) δ(q1, ε, Z) = (q2, ε) 

Nu gaan we deze PDA simuleren voor de invoerstring 'aaabbbbbb'.

 δ(q0, aaabbbbbb, Z) ⊢ δ(q0, aabbbbbb, aaZ) ⊢ δ(q0, abbbbbb, aaaaZ) ⊢ δ(q0, bbbbbb, aaaaaaZ) ⊢ δ(q1, bbbbb, aaaaaZ) ⊢ δ(q1, bbbb, aaaaZ) ⊢ δ(q1, bbb, aaaZ) ⊢ δ(q1, bb, aaZ) ⊢ δ(q1, b, aZ) ⊢ δ(q1, ε, Z) ⊢ δ(q2, ε) ACCEPT 

Voorbeeld 2:

Ontwerp een PDA die taal 0 accepteert^N1^M0^N.

Oplossing: In deze PDA wordt een aantal nullen gevolgd door een willekeurig aantal enen, gevolgd door een aantal nullen. Daarom zal de logica voor het ontwerp van een dergelijke PDA als volgt zijn:

Duw alle nullen op de stapel als je de eerste nullen tegenkomt. Als we dan 1 lezen, doe dan gewoon niets. Lees vervolgens 0, en bij elke lezing van 0, knalt u één 0 van de stapel.

Vlc mediaspeler download youtube

Bijvoorbeeld:

Dit scenario kan in de ID-vorm worden geschreven als:

 δ(q0, 0, Z) = δ(q0, 0Z) δ(q0, 0, 0) = δ(q0, 00) δ(q0, 1, 0) = δ(q1, 0) δ(q0, 1, 0) = δ(q1, 0) δ(q1, 0, 0) = δ(q1, ε) δ(q0, ε, Z) = δ(q2, Z) (ACCEPT state) 

Nu gaan we deze PDA simuleren voor de invoerstring '0011100'.

 δ(q0, 0011100, Z) ⊢ δ(q0, 011100, 0Z) ⊢ δ(q0, 11100, 00Z) ⊢ δ(q0, 1100, 00Z) ⊢ δ(q1, 100, 00Z) ⊢ δ(q1, 00, 00Z) ⊢ δ(q1, 0, 0Z) ⊢ δ(q1, ε, Z) ⊢ δ(q2, Z) ACCEPT