De normaalkracht wordt gedefinieerd als de kracht die door een oppervlak op een ander object wordt uitgeoefend. Wanneer een voorwerp in rust is, is de netto kracht die erop wordt uitgeoefend gelijk aan nul. Er kan geen normaalkracht worden uitgeoefend op twee oppervlakken die niet met elkaar verbonden zijn. Het kan worden geïnterpreteerd als een onderdeel van de kracht die verticaal staat op elk contactoppervlak. Het bepaalt hoeveel kracht het lichaam op de grond levert. De normaalkracht is alleen gelijk aan het gewicht van het object als de snelheidsverandering van het object negatief is, wat betekent dat het vertraagt.
Formule
De waarde van de normaalkracht hangt af van waar het object zich bevindt ten opzichte van het andere object. Wanneer een voorwerp gaat vallen, bepaalt de positie waarin het voorwerp op de grond valt de waarde van de normaalkracht. De normaalkracht wordt aangegeven met het symbool FN. De meeteenheid is Newton (N) en de maatformule wordt gegeven door [M1L1T-2].
Als een lichaam op een vlakke kracht rust, is de normaalkracht gelijk aan de waarde van het zwaartekrachtgewicht, dat wil zeggen mg.
F N = mg
waar,
FNis de normaalkracht,
m is de massa van het rustende object,
g is de versnelling als gevolg van de zwaartekracht.
Als een lichaam onder een bepaalde hoek van een schuin oppervlak naar beneden glijdt, is de waarde van de normaalkracht het zwaartekrachtgewicht toegevoegd door een extra kracht van F sin θ. In dit geval is de normaalkracht groter dan het gewicht van het object.
F N = mg + F zonde θ
Waar,
FNis de normaalkracht,
m is de massa van het glijdende object,
g is de versnelling als gevolg van de zwaartekracht,
θ is de hellingshoek.
Als de kracht in opwaartse richting op een lichaam inwerkt, is de waarde van de normaalkracht het zwaartekrachtgewicht verminderd met een kracht van F sin θ. In dit geval is de netto normaalkracht kleiner dan het gewicht van het object.
F N = mg – F zonde θ
waar,
voeg een watermerk in het woord inFNis de normaalkracht,
m is de massa van het glijdende object,
g is de versnelling als gevolg van de zwaartekracht,
θ is de hellingshoek.
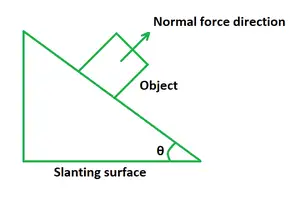
Als een lichaam op een hellend vlak wordt geplaatst, wordt de normaalkracht FNis gelijk aan het product van het zwaartekrachtgewicht en de cosinus van de hellingshoek.
F N = mg cosθ
waar,
FNis de normaalkracht,
m is de massa van het glijdende object,
g is de versnelling als gevolg van de zwaartekracht,
θ is de hellingshoek.
Voorbeeldproblemen
Probleem 1. Een voorwerp met een massa van 2 kg rust op een tafel. Bereken de normaalkracht die erop wordt uitgeoefend.
Oplossing:
We hebben,
m = 2
g = 9,8
Met behulp van de formule die we krijgen,
FN= mg
= 2 (9,8)
= 19,6 N
Opgave 2. Een voorwerp rust op een tafel met een kracht van 39,2 N. Bereken de normaalkracht die erop wordt uitgeoefend.
Oplossing:
We hebben,
F = 39,2
g = 9,8
Met behulp van de formule die we krijgen,
FN= mg
binaire boom postorder traversal=> m = F/g
=> meter = 39,2/9,8
=> m = 4 kg
Probleem 3. Een voorwerp met een massa van 10 kg glijdt met een kracht van 200 N naar beneden vanaf een schuin oppervlak onder een hoek van 30°. Bereken de normaalkracht die erop wordt uitgeoefend.
Oplossing:
We hebben,
F = 200
m = 10
g = 9,8
θ = 30°
Met behulp van de formule die we krijgen,
FN= mg + F zonde θ
= 10 (9,8) + 200 op 30°
= 98 + 200 (1/2)
= 98 + 100
= 198 N
Probleem 4. Een voorwerp met een massa van 20 kg glijdt met een kracht van 400 N naar beneden vanaf een schuin oppervlak onder een hoek van 30°. Bereken de normaalkracht die erop wordt uitgeoefend.
Oplossing:
We hebben,
F = 400
meter = 20
g = 9,8
θ = 30°
Met behulp van de formule die we krijgen,
FN= mg + F zonde θ
= 20 (9,8) + 400 zonde 30°
= 196 + 400 (1/2)
= 196 + 200
= 396 N
Opgave 5. Een voorwerp met een massa van 15 kg wordt op een schuin oppervlak geplaatst onder een hoek van 30°. Bereken de normaalkracht die erop wordt uitgeoefend als de kracht naar boven werkt met een waarde van 100 N.
Oplossing:
We hebben,
F = 100
m = 15
g = 9,8
θ = 30°
Met behulp van de formule die we krijgen,
FN= mg – F zonde θ
Freddie Mercury geboren= 15 (9,8) – 100 zonder 30°
= 147 – 100 (1/2)
= 147 – 50
= 97 N
Opgave 6. Een voorwerp met een massa van 5 kg wordt op een schuin oppervlak geplaatst onder een hoek van 60°. Bereken de normaalkracht die er op een bepaald punt op wordt uitgeoefend.
Oplossing:
We hebben,
m = 5
g = 9,8
θ = 60°
Met behulp van de formule die we krijgen,
FN= mg cosθ
= 5 (9,8) (cos 60°)
= 49/2
= 24,5 N
Probleem 7. Een voorwerp wordt op een schuin oppervlak geplaatst onder een hoek van 60°. Bereken zijn massa als de normaalkracht die erop wordt uitgeoefend 400 N bedraagt.
Oplossing:
We hebben,
FN= 400,
θ = 60°
Met behulp van de formule die we krijgen,
FN= mg cosθ
m = F/(g cos θ)
= 400/ (9,8 × cos 60°)
= 400/4,9
= 81,63 N
