Voor het weergeven van cijfers kan een uit zeven segmenten bestaand display worden gebruikt. Gegeven een array van N natuurlijke getallen. De taak is om het getal in de array te vinden dat het minimumaantal segmenten gebruikt om het getal weer te geven. Als meerdere getallen een minimumaantal segmenten hebben, wordt het getal met de kleinste index uitgevoerd.
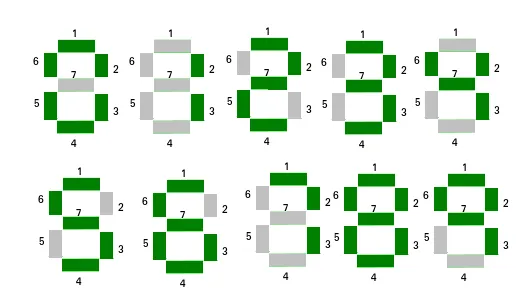
Voorbeelden:
Invoer: arr[] = { 1 2 3 4 5 }.
Uitgang: 1
Uitleg: Het element dat het minimum aantal segmenten gebruikt is 1 (d.w.z. 2 segmenten)Invoer: arr[] = { 489 206 745 123 756 }.
Uitgang: 745
Uitleg: Het element met de kleinste index dat het minimum aantal segmenten gebruikt is 745 (d.w.z. 12 segmenten)
Het idee is om vooraf het aantal segmenten te berekenen dat wordt gebruikt door de cijfers van 0 tot en met 9 en dit op te slaan. Tel nu voor elk element van de array het aantal segmenten op dat door elk cijfer wordt gebruikt. Zoek vervolgens het element dat het minimumaantal segmenten gebruikt.
C++Het aantal segmenten dat per cijfer wordt gebruikt:
0 -> 6
1 -> 2
2 -> 5
3 -> 5
4 -> 4
5 -> 5
6 -> 6
7 -> 3
8 -> 7
9 -> 6
#include
import java.io.*; class GFG { // Precomputed values of segment // used by digit 0 to 9. static int []seg = { 6 2 5 5 4 5 6 3 7 6}; // Return the number of segments used by x. static int computeSegment(int x) { if (x == 0) return seg[0]; int count = 0; // Finding sum of the segment used by // each digit of a number. while (x > 0) { count += seg[x % 10]; x /= 10; } return count; } static int elementMinSegment(int []arr int n) { // Initialising the minimum segment // and minimum number index. int minseg = computeSegment(arr[0]); int minindex = 0; // Finding and comparing segment used // by each number arr[i]. for (int i = 1; i < n; i++) { int temp = computeSegment(arr[i]); // If arr[i] used less segment then update // minimum segment and minimum number. if (temp < minseg) { minseg = temp; minindex = i; } } return arr[minindex]; } static public void main (String[] args) { int []arr = {489 206 745 123 756}; int n = arr.length; System.out.println(elementMinSegment(arr n)); } }
# Precomputed values of segment # used by digit 0 to 9. seg = [6 2 5 5 4 5 6 3 7 6] # Return the number of # segments used by x. def computeSegment(x): if(x == 0): return seg[0] count = 0 # Finding sum of the segment # used by each digit of a number. while(x): count += seg[x % 10] x = x // 10 return count # function to return minimum sum index def elementMinSegment(arr n): # Initialising the minimum # segment and minimum number index. minseg = computeSegment(arr[0]) minindex = 0 # Finding and comparing segment # used by each number arr[i]. for i in range(1 n): temp = computeSegment(arr[i]) # If arr[i] used less segment # then update minimum segment # and minimum number. if(temp < minseg): minseg = temp minindex = i return arr[minindex] # Driver Code arr = [489 206 745 123 756] n = len(arr) # function print required answer print(elementMinSegment(arr n)) # This code is contributed by # Sanjit_Prasad
using System; class GFG{ // Precomputed values of segment // used by digit 0 to 9. static int []seg = new int[10]{ 6 2 5 5 4 5 6 3 7 6}; // Return the number of segments used by x. static int computeSegment(int x) { if (x == 0) return seg[0]; int count = 0; // Finding sum of the segment used by // each digit of a number. while (x > 0) { count += seg[x % 10]; x /= 10; } return count; } static int elementMinSegment(int []arr int n) { // Initialising the minimum segment // and minimum number index. int minseg = computeSegment(arr[0]); int minindex = 0; // Finding and comparing segment used // by each number arr[i]. for (int i = 1; i < n; i++) { int temp = computeSegment(arr[i]); // If arr[i] used less segment then update // minimum segment and minimum number. if (temp < minseg) { minseg = temp; minindex = i; } } return arr[minindex]; } static public void Main() { int []arr = {489 206 745 123 756}; int n = arr.Length; Console.WriteLine(elementMinSegment(arr n)); } }
// Precomputed values of segment // used by digit 0 to 9. let seg = [ 6 2 5 5 4 5 6 3 7 6]; // Return the number of segments used by x. function computeSegment(x) { if (x == 0) return seg[0]; let count = 0; // Finding sum of the segment used by // each digit of a number. while (x > 0) { count += seg[x % 10]; x = parseInt(x / 10 10); } return count; } function elementMinSegment(arr n) { // Initialising the minimum segment // and minimum number index. let minseg = computeSegment(arr[0]); let minindex = 0; // Finding and comparing segment used // by each number arr[i]. for(let i = 1; i < n; i++) { let temp = computeSegment(arr[i]); // If arr[i] used less segment then update // minimum segment and minimum number. if (temp < minseg) { minseg = temp; minindex = i; } } return arr[minindex]; } // Driver code let arr = [ 489 206 745 123 756 ]; let n = arr.length; console.log(elementMinSegment(arr n));
Uitvoer
745
Tijdcomplexiteit: O(n * log 10 N)
Hulpruimte: O(10)
