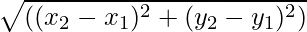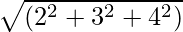Vectorgrootheden zijn de grootheden die zowel richting als grootte hebben. De grootte van een vector is de lengte van de vector. Het wordt gegeven door de numerieke waarde van de vector en omdat het de lengte van de vector vertegenwoordigt, is het altijd positief. Voor elke vector 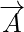de omvang ervan wordt weergegeven als .

Laten we in dit artikel meer leren over de omvang van de vector, de formule, voorbeelden en andere.

Inhoudsopgave

• Wat is de grootte van een vector?
• Omvang van een vectorformule
• Richting van een vector
• Hoe de grootte van een vector vinden?
• Opgeloste voorbeelden

Wat is de grootte van een vector?

De grootte van een vector wordt gedefinieerd als de lengte van de vector. Omdat de grootte van de vector de lengte van de vector aangeeft, is deze altijd positief. Voor elke vector A wordt de grootte weergegeven als |A|. Stel dat een vector wordt gedefinieerd als xi + yj, dan wordt de grootte ervan gedefinieerd als de vierkantswortel van de som van de kwadraten van de afzonderlijke termen. De grootte van de vector vertegenwoordigt de lengte van de vector, dat wil zeggen de waarde of impact die de vector heeft.

Als er bijvoorbeeld een kracht van 5i N op een object werkt, dan is de grootte ervan 5 N, wat betekent dat de kracht van de uitgeoefende kracht 5 N is, en ‘ i' in 5i betekent dat het wordt toegepast in de positieve x-richting.

Omvang van een vectorformule

Er zijn verschillende manieren om de grootte van de vector te berekenen. Gebruik op basis van de gegeven gegevens een ander soort formule om de grootte van een vector te vinden. De grootte van een vector A wordt weergegeven met behulp van de modulusoperator, d.w.z. |A|

Er zijn verschillende formules die worden gebruikt om de grootte van de vector te tellen. De volgende afbeelding toont de belangrijke formules die worden gebruikt om de grootte van de vector te vinden.

Hieronder volgen manieren om de omvang te berekenen.

• Als ze een vector Ā = xi+ yĵ + zk̂ krijgen, dan kan de grootte van vector Ā worden berekend met behulp van de onderstaande formule

Grootte van vector  (|A|) = √(x ² + en ² +z ² )

• Als de startpuntvector bijvoorbeeld (x₁, En₁) en het eindpunt van een vector is bijvoorbeeld (x₂, En₂) wordt vervolgens de grootte van de vector gegeven is gegeven door,

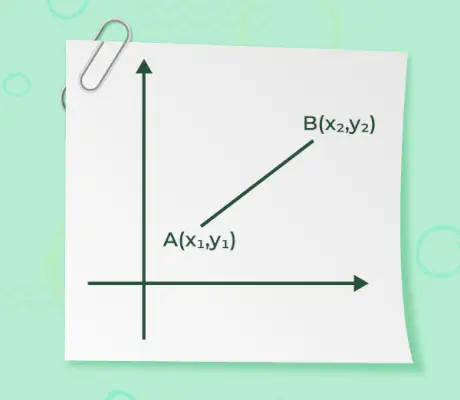
De grootte van een vector, wanneer het begin- en eindpunt van een vector gegeven zijn, is niets anders dan de afstand tussen de punten. De formule voor het vinden van de omvang wordt gegeven door

=

• Als een van de begin- of eindpunten van een vector de oorsprong o(0, 0) heeft en een ander punt dat is EEN(x, y) zoals gespecificeerd in de onderstaande afbeelding,

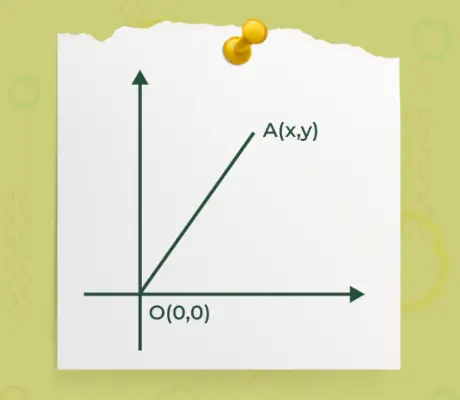
Vervolgens wordt de formule voor het vinden van de grootte van een vector waarbij een van de uiteinden van een vector zich in de oorsprong bevindt, gegeven door

|À| = √(x ² +y ² )

Richting van een vector

Vectorgrootheden zijn grootheden die zowel grootheden als richtingen hebben. De richting van de vectorhoeveelheid geeft aan in welke richting de vectorhoeveelheid wordt toegepast. Het wordt gedefinieerd als de hoek die de vector maakt met de horizontale lijn of de x-as. Het wordt weergegeven door het symbool A .

De onderstaande afbeelding toont de pijl die wordt gebruikt om de richting van de vector aan te geven.

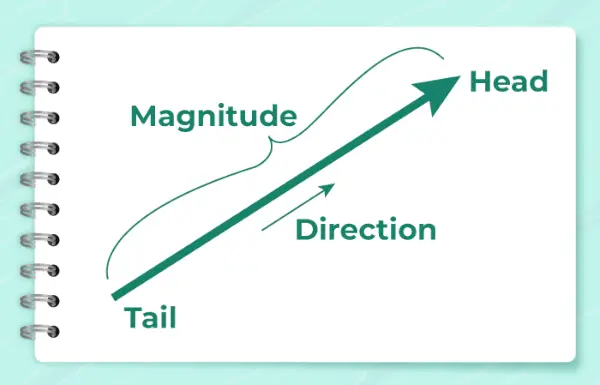
Het wordt berekend met behulp van de formule,

α = bruin ^-1 (y/x)

voorwaardelijke operator in Java

Voor de vector gegenereerd door de coördinaten (x₁, En₁) en (x₂, En₂) hun richting wordt gegeven door de formule,

uitvoerend

α = bruin ^-1 [(En ₂ - En ₁ )/(X ₂ - X ₁ )]

Hoe de grootte van een vector vinden?

De grootte van de vector wordt berekend met behulp van de hieronder besproken stappen,

Stap 1: Identificeer de x-, y- en z-componenten van de vector.

Stap 2 : Zoek het kwadraat van alle x-, y- en z-componenten.

Stap 3: Voeg alle vierkanten toe die je in stap 2 hebt gevonden.

Stap 4: Zoek de vierkantswortel van de som verkregen in stap 3.

De waarde die na stap 4 wordt verkregen, is de grootte van de gegeven vector.

Voorbeeld: Zoek de grootte van de vector A = 3i + 4j

Oplossing:

De grootte van vector A wordt berekend met behulp van de hierboven besproken stappen.

Stap 1: Als we A = 3i + 4j vergelijken met xi + yj, krijgen we x = 3 en y = 4

Stap 2: X²= 3²= 9 en y²= 4²= 16

Stap 3: X²+ en²= 9 + 16 = 25

Stap 4: √(25) = 5

De grootte van de vector A = 3i + 4j is dus 5 eenheden.

Conclusie

Concluderend: de grootte van een vector vertelt ons hoe lang de vector is. Dit concept is erg belangrijk op veel gebieden, zoals natuurkunde, techniek en informatica, omdat het helpt zaken als snelheid, kracht en bewegingsrichting te meten. Door de omvang van vectoren te begrijpen, kunnen we praktische problemen beter analyseren en oplossen, waardoor het een belangrijk stukje kennis wordt voor iedereen die met getallen en metingen werkt in toepassingen in de echte wereld.

Lees verder,

• Scalair en vector
• Vectoroperaties
• Hoe bereken je de eenheidsvector?

Opgeloste voorbeelden van de omvang van vector

Voorbeeld 1: Vind de grootte van de vector Ā = 2i + 3ĵ + 4k.

Oplossing:

string naar geheel getal java

Gegeven,

Ā = 2i + 3ĵ + 4k

Omvang |A| =

=
= √29
= 5,38

De grootte van vector 2i+3ĵ+4k is 5.38 eenheid

Voorbeeld 2: Vind de grootte van de vector Ā = 3i + 3ĵ – 6k

Oplossing:

Gegeven

Ā = 3i + 3ĵ – 6k

Omvang |A| =

=
= √54
= 7,35

De grootte van vector 3i+ 3ĵ – 6k is 7.35 eenheid.

Voorbeeld 3: Vind de grootte van de vector als het beginpunt van een vector (3, 4) is en het eindpunt (6, 2).

Oplossing:

Gegeven,

(X₁, En₁) = (3, 4)
(X₂, En₂) = (6, 2)

|Ā|=

=
= √(3²+ (-2)²)
= √(9+4)
= √13 = 3,6

De grootte van de gegeven vector is dus 3.6 eenheid.

Voorbeeld 4: Vind de grootte van de vector als het startpunt van een vector (2, 1, 4) is en het eindpunt (5, 2, 6).

Oplossing:

Gegeven,

(X₁, En₁, Met₁) = (2, 1, 4)

statisch Java

(X₂, En₂, Met₂) = (5, 2, 6)

|À| =

=
=
= √(9 +1 + 4)
= √14 = 3,74

De grootte van de gegeven vector is dus 3,74 eenheid.

Voorbeeld 5: Wat is de grootte van de vector die begint bij de oorsprong en het eindpunt bij (3, 4).

Oplossing:

Gegeven,

Startpunt van vector is O(0, 0)

Eindpunt (x, y) = (3, 4)

Grootte van vector (|Ā|) = √(x²+y²)

= √(3²+ 4²)
= √(9 + 16)
= √25 = 5

De grootte van de gegeven vector is dus 5 eenheid.

Voorbeeld 6: Zoek de grootte van de vector waarin een van de eindpunten zich in de oorsprong bevindt en het andere punt in (1, 4, 3).

Oplossing:

Gegeven,

Eindpunt van vector is O(0, 0)

Ander punt (x, y, z) = (1, 4, 3)

Grootte van vector (|Ā|) = √(x²+y²+z²)

=
=
= √26 = 5,09

De grootte van de gegeven vector is dus 5.09 eenheid.

afbeeldingen centreren in css

Veelgestelde vragen over de grootte van een vector

Wat is de grootte van een vectorformule?

De grootte van een vector is de numerieke waarde van de vector en definieert de lengte van de vector. Voor elke vector wordt de grootte van A weergegeven als |A|. De grootte van de vector wordt berekend met behulp van de formule:

Voor elke vector, A = xi + yj + zk, wordt de grootte ervan gegeven door de formule

|EEN| = √(x ² + en ² + z ² )

Voor elke vector waarvan het begin- en eindpunt respectievelijk (x₁, En₁) en (x₂, En₂) de omvang ervan wordt gegeven door de formule

|EEN| = √((x ₂ - X ₁ ) ² + (en ₂ - En ₁ ) ² )

Hoe kan de omvang van een vector worden weergegeven?

De grootte van de vector A wordt weergegeven door het symbool |A|.

Hoe vind je de grootte van een vector?

Er worden verschillende formules gebruikt om de grootte van de vector te berekenen, sommige zijn:

• |EEN| = √(x ² + en ² + z ² ) wanneer de vector de vorm heeft van A = xi + yj + zk
• |EEN| = √((x) ² + (en) ² ) wanneer de vector wordt gegeven door punt A (x, y) en de oorsprong O(0, 0).
• |EEN| = √((x ₂ - X ₁ ) ² + (en ₂ - En ₁ ) ² ) wanneer de vector wordt gegeven door punt A (x₁, En₂) en punt B (x₂, En₂).

Zoek een vector van magnitude 5.

Er zijn verschillende vectoren die een grootte van 5 kunnen hebben, waarvan een voorbeeld vector A is, weergegeven als:

A = 3i + 4j Of A = 4i + 5j