Minder dan teken, aangegeven als <, is een wiskundig symbool dat een ongelijkheid tussen twee waarden aangeeft. Wanneer we het <-symbool gebruiken, betekent dit dat de waarde of hoeveelheid aan de linkerkant kleiner is dan de waarde aan de rechterkant.
Laten we bespreken Minder dan symbool , de toepassingen ervan in ongelijkheden, samen met enkele opgeloste voorbeelden.
Inhoudsopgave
- Wat is minder dan symbool?
- Minder dan symboolvoorbeelden
- Tabel met wiskundige tekens - Kleiner dan, groter dan en gelijk aan
- Hoe onthoud je minder dan een symbool?
- Kleiner dan, groter dan en gelijk aan symbolen
- Minder dan symbool in ongelijkheid
- Minder dan symboolvragen
Wat is minder dan symbool?
Kleiner dan teken (<) is een symbool dat tussen twee waarden wordt gebruikt, wat betekent dat de linkerwaarde kleiner is dan de rechterwaarde.
- <-symbool geeft kleiner dan aan.
- Minder-dan-symbool, aangeduid als (<) , wordt gebruikt om de relatie tussen twee getallen of hoeveelheden weer te geven.
- Kleiner dan symbool is binair, wat betekent dat er twee operanden nodig zijn, en wordt gelezen als minder dan of kleiner dan.
Minder dan symboolbetekenis
Het kleiner dan-symbool (<) wordt in de wiskunde gebruikt om aan te geven dat de waarde aan de linkerkant van het symbool kleiner is dan de waarde aan de rechterkant. In de uitdrukking 3<53<5 wordt bijvoorbeeld gesteld dat 3 kleiner is dan 5.
Minder dan symboolvoorbeelden
Hier zijn enkele voorbeelden van Minder dan symbool:
- 3 <5 (Drie is minder dan vijf)
- -2 <0 (negatieve twee is kleiner dan nul)
- 7 <7 (Zeven is niet minder dan zeven. Het is gelijk aan zeven)
Tabel met wiskundige tekens - Kleiner dan, groter dan en gelijk aan
De volgende tabel geeft de wiskundige tekens ter vergelijking weer, samen met hun naam, betekenis en voorbeelden.
| Wiskundige tekens – Betekenis en voorbeelden | |||
|---|---|---|---|
| Symbool/teken | < | = | > |
| Naam | minder dan | is gelijk aan | groter dan |
| Duidt op | linkerwaarde is kleiner dan rechterwaarde | linker- en rechterwaarden zijn gelijk | linkerwaarde is groter dan rechterwaarde |
| Voorbeeld | 5 <7 | 5 = 5 | 7> 5 |
Hoe onthoud je minder dan een symbool?
Kleiner dan teken en zijn tegenhanger groter dan hebben een vrijwel vergelijkbare visuele weergave, maar in tegengestelde richting. Om verwarring te voorkomen zijn er daarom twee trucjes waarmee we ons kunnen herinneren wat het teken van Minder Dan is.
Deze methoden worden genoemd L-methode En Kleinere mondmethode.
L Methode voor kleiner dan symbool
Deze methode is eenvoudig – minder dan begint met een letter L, dus het symbool dat het meest op een lijkt L is degene die dat betekent minder dan .
Gesloten mond Methode voor minder dan symbool
Gesloten mond aan de linkerkant geeft minder dan symbool aan. Het gesloten uiteinde van < wijst naar de kleinere hoeveelheid.

Kleiner dan, groter dan en gelijk aan symbolen
Nu gaan we in het kort groter dan, kleiner dan en gelijk aan teken bespreken.
- Groter dan teken
- Minder dan teken
- Gelijk aan Teken
Groter dan teken
Groter dan teken> wordt gebruikt om een specifiek type vergelijking tussen twee grootheden uit te drukken, waarbij de linkerwaarde groter is dan de rechterwaarde.
Voorbeeld: 10> 5; (tien is groter dan vijf)
Minder dan teken
Minder dan teken < wordt gebruikt om een specifiek type vergelijking tussen twee grootheden uit te drukken, waarbij de linkerwaarde kleiner is dan de rechterwaarde.
Voorbeeld: 5 <10; (vijf is minder dan 10)
Gelijk aan Teken
Gelijk aan Teken = wordt gebruikt om de gelijkheid tussen twee getallen of waarden weer te geven. Het geeft aan dat zowel de linker- als de rechterwaarde gelijk zijn.
Voorbeeld: 5 + 5 = 10, d.w.z. 10 = 10 (tien is gelijk aan tien)
Hierboven staan de fundamentele tekens die ter vergelijking worden gebruikt. Er zijn andere tekens die worden gevormd door een combinatie van tekens. Dit zijn groter dan gelijk aan En minder dan gelijk aan.
Kleiner dan of gelijk aan symbool
Kleiner dan of gelijk aan symbool ≤ wordt gebruikt als er onduidelijkheid bestaat tussen de grootte van de hoeveelheid. Laten we zeggen dat we een verklaring hebben waarin staat dat het aantal appels dat Ram heeft kleiner is dan of gelijk is aan dat van Rohan. Dan kunnen we het wiskundig uitdrukken als x ≤ y waarbij x het aantal appels is met Ram en y het aantal appels met Rohan.
Niet minder dan symbool
Niet minder dan symbool ≮ wordt gebruikt als de hoeveelheid aan de linkerkant niet kleiner is dan de hoeveelheid aan de rechterkant. Dit betekent dat de hoeveelheid aan de linkerkant gelijk is aan of groter is dan de hoeveelheid aan de rechterkant.
Laten we zeggen dat de leeftijd van John ‘p’ jaar is en Andrew ‘q’ jaar oud is en de leeftijd van John niet minder is dan de leeftijd van Andrew. Dit betekent dat de leeftijd van John gelijk is aan of groter is dan die van Andreas. We kunnen het wiskundig uitdrukken als p ≮ q.
Lees gedetailleerd: Groter dan en kleiner dan symbolen
Minder dan symbool in ongelijkheid
Een ongelijkheid is een verklaring die twee uitdrukkingen vergelijkt, en het kleiner dan-symbool geeft aan dat de uitdrukking aan de linkerkant kleiner is dan die aan de rechterkant. Het minder dan-symbool wordt vaak gebruikt bij wiskundige ongelijkheden
Soorten ongelijkheden
De ongelijkheden zijn van twee soorten, genaamd:
- Strenge ongelijkheid
- Niet-strikte ongelijkheid
Deze twee ongelijkheden worden hieronder besproken:
Strikte ongelijkheid (<)
Dit type ongelijkheid vertegenwoordigt een situatie waarin de linkerkant strikt kleiner is dan de rechterkant.
Bijvoorbeeld:
- 2 <7
- x <10; x is kleiner dan 10, dit betekent dat x -∞ tot 9 kan zijn
Strenge ongelijkheid op de getallenlijn
Om ongelijkheden te visualiseren met behulp van het kleiner dan-symbool, kunt u de getallen op een getallenlijn uitzetten. De getallenlijn biedt een grafische weergave van hoe waarden zich tot elkaar verhouden.
Laten we een voorbeeld bekijken:
x<4. Deze ongelijkheid betekent dat de waarde van x kleiner is dan 4. Op de getallenlijn zou je dit weergeven door het gebied links van 4 te arceren.

Niet-strikte ongelijkheid (≤)
In dit geval kan de linkerkant kleiner zijn, maar kan deze ook gelijk zijn aan de rechterkant.
Bijvoorbeeld: 3 ≤ 3 (Drie is kleiner dan of gelijk aan drie).
Niet-strikte ongelijkheid op de getallenlijn
Laten we een voorbeeld bekijken:
x ≤ 4, deze ongelijkheid betekent dat de waarde van x kleiner is dan of gelijk is aan 4 (inclusief 4). Op de getallenlijn zou je dit weergeven door het gebied links en op de 4 te arceren.

Minder dan symboolvoorbeelden
Hier hebben we enkele voorbeeldvragen opgelost die u kunt leren.
Voorbeeld 1: Hoe representeer je 10 is symbolisch minder dan 50?
Oplossing:
10 is minder dan 50 wordt symbolisch weergegeven als 10 <50
Voorbeeld 2: Bepaal of de volgende uitspraken waar of onwaar zijn:
A) 8 <12
B) -5 <-7
C) 6 <6
Oplossing:
a) Waar (8 is minder dan 12)
b) Onwaar (-5 is niet minder dan -7)
c) Onwaar (6 is niet minder dan 6; ze zijn gelijk)
Voorbeeld 3: Vind het mogelijke gehele getal voor ‘x’; waar 10
Oplossing:
Gegeven, 10
Vanaf 10
Vanaf x <15 kan x zijn: (-∞….. 9, 10, 11, 12, 13, 14, 15)
Als we het bereik nemen van zowel de verklaring die we krijgen x kan zijn: 11, 12, 13, 14, 15, 16
Voorbeeld 4: Los op voor x: 3x <15
Oplossing:
Om de waarde van x te vinden, deelt u beide zijden van de ongelijkheid door 3:
3x <15
x <15 / 3
x<5
Dus de oplossing is x<5
Voorbeeld 5: Een rechthoekige tuin is 3 meter lang en 2,5 meter breed. Een andere rechthoekige tuin is 4,5 meter lang en 3 meter breed. Welke tuin heeft een kleinere oppervlakte?
Oplossing:
Om de oppervlakten te vergelijken, berekent u de oppervlakten van beide tuinen
slf4j versus log4jDe eerste tuin heeft een oppervlakte van 12 voet x 8 voet = 96 vierkante voet
De tweede tuin heeft een oppervlakte van 15 voet x 10 voet = 150 vierkante voet
Dat weten we, 96 <150
De eerste tuin heeft een kleiner oppervlak omdat 96 minder is dan 150
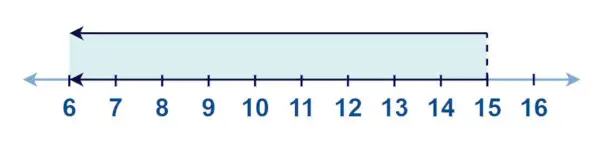
Voorbeeld 6: Voor x <15 tekent u voor x op de getallenlijn.
Oplossing:
Op de getallenlijn wordt x <15 getekend als:

Minder dan symboolvragen
Hier zijn enkele vragen over Less Than Sign voor uw praktijk.
Q1. Ram heeft 5 toffees en Shyam heeft 8 toffees. Wie heeft minder toffees?
Vraag 2. Bob slaapt een half uur en Alice slaapt elke dag in de middag 60 minuten. Wie slaapt minder lang?
Q3. Geef aan of de gegeven bewering waar of onwaar is:
- 5 <8
- 10 <7
- x <100 ; waarbij x = 20
Q4. Zoek het mogelijke gehele getal voor ‘x’; waar 5
Vraag 5. Teken voor ‘x’ op de getallenlijn; waarbij x <100.
Vraag 6. Plaats het Groter dan of Kleiner Tham-symbool in het volgende
- 2__5
- 0,25 __ 0,252
- -14 __ 0
- 1/4 __ 1/3
Mensen lezen ook:
- Groter dan en kleiner dan symbolen
- Gelijkteken
- Meer dan teken
Veelgestelde vragen over Less Than Symbol
Wat vertegenwoordigt Less Than Sign in de wiskunde?
Kleiner dan teken (<) is een wiskundig symbool dat wordt gebruikt om aan te geven dat de linkerwaarde kleiner of kleiner is dan de rechterwaarde.
Wat is het tegenovergestelde van Minder dan symbool?
Het tegenovergestelde van het kleiner dan-symbool (), dat aangeeft dat de ene waarde groter is dan de andere.
Hoe ziet Minder dan symbool eruit?
Minder dan het symbool ziet eruit als een gekantelde ‘L’. Raadpleeg de afbeelding in het artikel.
Wat is het gebruik van kleiner dan teken?
Kleiner dan-teken (<) wordt gebruikt om aan te geven dat de ene waarde kleiner is dan de andere. In de uitspraak 3 < 5 betekent dit bijvoorbeeld dat 3 kleiner is dan 5.
Wat is het verschil tussen symbolen van groter dan, kleiner dan en gelijk aan?
Het groter dan-symbool (>) geeft aan dat de waarde aan de linkerkant groter is dan de waarde aan de rechterkant, terwijl het kleiner dan-symbool (<) aangeeft dat de waarde aan de linkerkant kleiner is dan de waarde aan de rechterkant. Het gelijk aan-symbool (=) geeft aan dat de waarden aan beide zijden exact hetzelfde zijn.
Kan Less Than Symbol worden gebruikt met variabelen?
Ja, het minder dan-symbool kan worden gebruikt bij ongelijkheden waarbij variabelen betrokken zijn. x <10 betekent bijvoorbeeld dat de variabele x kleiner is dan 10.
Wat is het verschil tussen strikte en niet-stricte ongelijkheden?
Bij een strikte ongelijkheid (bijvoorbeeld x <5) moet de linkerwaarde strikt kleiner zijn dan de rechterwaarde. Bij een niet-strikte ongelijkheid (bijvoorbeeld x ≤ 5) kan de linkerwaarde gelijk zijn aan de rechterwaarde.
