Is elke rechthoek een ruit? Rechthoek is een tweedimensionale geometrische figuur weergegeven door vier zijden en vier hoeken. Een rechthoek bevat zijden zodat de lengte van de tegenoverliggende zijden gelijk is en deze zijden evenwijdig aan elkaar zijn. De zijden delen een hoek van aangrenzende zijden met een hoek van 90° daartussen. Daarom zijn er vier rechte hoeken in de rechthoek.

Inhoudsopgave
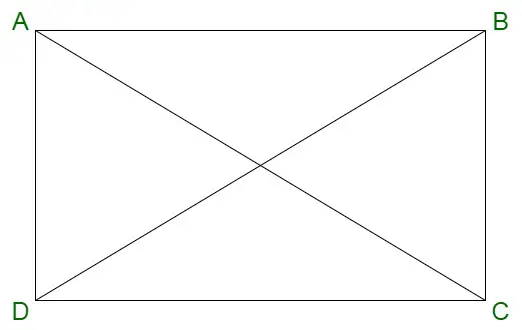
Rechthoek
De eigenschappen van een rechthoek worden hieronder gegeven:
- Het heeft vier randen en vier hoeken, ook wel hoekpunten genoemd.
- Diagonalen van een rechthoek snijden elkaar doormidden.
- De oppervlakte van een rechthoek is gelijk aan het product van zijn lengte en breedte.
- Elk hoekpunt heeft een hoek gelijk aan 90O
- De tegenoverliggende zijden van een rechthoek zijn gelijk en evenwijdig aan elkaar.
- De omtrek is gelijk aan tweemaal de som van de lengte en breedte.
- De som van alle binnenhoeken is gelijk aan 360 graden
Omtrek van een rechthoek
De totale verplaatsing die wordt afgelegd door de grens van de rechthoek te passeren, kan de omtrek worden genoemd. Omdat zowel lengte als breedte worden aangegeven met lengte-eenheid, wordt de omtrek ook gemeten in lengte-eenheid.
Omtrek kan worden aangegeven met,
Omtrek, P = 2 (lengte + breedte)
Gebied van rechthoek
Het gebied dat door een tweedimensionale geometrische figuur in een vlak wordt bedekt, wordt de oppervlakte van een figuur genoemd. De oppervlakte van een rechthoek is dus de oppervlakte binnen de grenzen ervan. Het wordt gemeten in vierkante eenheden. De oppervlakte is gelijk aan het product van de lengte en breedte van de rechthoek.
Gebied kan worden aangegeven met,
Oppervlakte, A = Lengte × Breedte vierkante eenheden
Diagonaal van een rechthoekformule
Diagonalen van elke geometrische figuur verbinden alternatieve hoekpunten. De lengte van de diagonalen van een rechthoek kan worden berekend met de volgende formule, aangegeven met d,
d = sqrt{( l^2 + w^2)} waar,
l = lengte van de rechthoek
w = breedte van de rechthoek
Lees in detail: Eigenschappen van rechthoek: definitie, formules, voorbeelden
Ruit
Een ruit wordt ook wel een vierzijdige vierhoek genoemd. Het wordt beschouwd als een speciaal geval van een parallellogram. Een ruit bevat parallelle tegenoverliggende zijden en gelijke tegenoverliggende hoeken. Een ruit is ook bekend onder de naam diamant of ruitdiamant. Een ruit bevat alle zijden van een ruit die even lang zijn. Ook snijden de diagonalen van een ruit elkaar loodrecht.
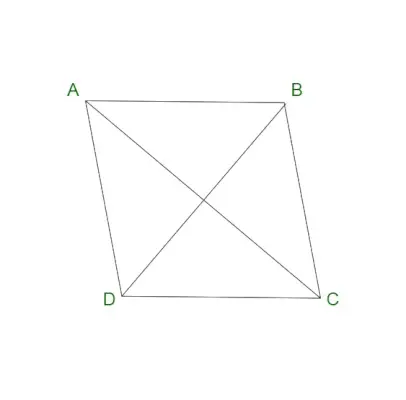
Eigenschappen van een ruit
Een ruit bevat de volgende eigenschappen:
- Een ruit bevat alle gelijke zijden.
- Diagonalen van een ruit snijden elkaar in een rechte hoek.
- De tegenoverliggende zijden van een ruit zijn parallel van aard.
- De som van twee aangrenzende hoeken van een ruit is gelijk aan 180O.
- Er is geen inschrijfcirkel binnen een ruit.
- Er bestaat geen omschrijvende cirkel rond een ruit.
- De diagonalen van een ruit leiden tot de vorming van vier rechthoekige driehoeken.
- Deze driehoeken zijn congruent met elkaar.
- De tegenovergestelde hoeken van een ruit zijn gelijk.
- Wanneer je het middelpunt van de zijkanten van een ruit met elkaar verbindt, ontstaat er een rechthoek.
- Wanneer de middelpunten van de helft van de diagonaal met elkaar verbonden zijn, ontstaat er weer een ruit.
Omtrek van Ruit
De omtrek van een ruit wordt gedefinieerd als de totale lengte van de grenzen die de figuur vormen. Het kan ook worden aangeduid als de totale som van de lengte van vier zijden van een ruit. De omtrek van een ruit wordt gedefinieerd door:
Omtrek, P = 4a eenheden
waarbij de diagonalen van de ruit worden aangegeven met d1& D2en ‘a’ is de zijkant.
Gebied van Ruit
Het gebied van de ruit wordt gedefinieerd als het gebied dat is ingesloten in een tweedimensionaal vlak. De oppervlakte van een ruit is gelijk aan het product van de diagonalen van de ruit gedeeld door 2. De oppervlakte van de ruit kan worden gedefinieerd met de volgende formule:
Oppervlakte, A =
frac{(d_1 imes d_2)}{2} vierkante eenhedenwaar d1en d2zijn de diagonalen van een ruit.
We kunnen gemakkelijk opmerken dat elke ruit een parallellogram is, maar het omgekeerde is niet waar. Een vierkant kan worden beschouwd als een speciaal geval van een ruit, omdat het vier zijden van gelijke lengte bevat. Een vierkant heeft allemaal rechte hoeken. Alle hoeken van een ruit zijn echter niet noodzakelijkerwijs rechte hoeken . Concluderend kan een ruit met rechte hoeken als een vierkant worden beschouwd. Daarom kunnen we zeggen dat,
- Alle ruiten zijn parallellogrammen.
- Alle parallellogrammen zijn geen ruiten.
- Niet alle ruiten zijn vierkanten.
- Alle vierkanten zijn ruiten.
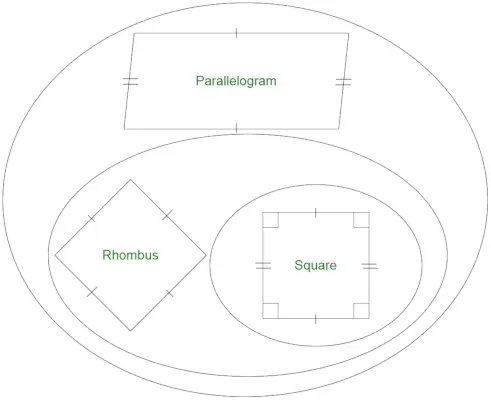
Is elke rechthoek een ruit?
Een rechthoek is een geometrische figuur die niet alle gelijke zijden bevat. Een vierkant is een speciaal geval van een rechthoek met allemaal gelijke zijden. Omdat we weten dat een ruit allemaal gelijke zijden heeft. De sets rechthoeken en ruiten snijden elkaar alleen in het geval van vierkanten. Daarom is de rechthoek geen ruit.
leer selenium

Waarom is een ruit een rechthoek?
Een ruit is een speciaal geval van een rechthoek. Omdat we weten dat de diagonalen van een ruit elkaar onder gelijke hoeken snijden, terwijl de diagonalen van een rechthoek even lang zijn. Door de middelpunten van de zijkanten van een ruit met elkaar te verbinden, wordt een rechthoek gevormd.
Lees meer: Waarom is een ruit geen vierkant?
Voorbeeldvragen – Is elke rechthoek een ruit?
Vraag 1. Bereken de oppervlakte van een rechthoekig frame met een diameter van 15 cm lengte en is 3 inch breed.
Oplossing:
Aangezien we weten,
Oppervlakte van een rechthoek = (lengte x breedte) vierkante eenheden.
Door de waarden te vervangen, verkrijgen we:
de oppervlakte van het rechthoekige frame = 6 × 3 = 18 vierkante inch
Vraag 2. Zoek de lengte van de diagonaal van een rechthoek met een lengte van respectievelijk 12 cm en een breedte van 8 cm.
Oplossing:
Wij weten,
diagonale lengte,
D =
sqrt{ L^2+W^2} ⇒ D =
sqrt{12^2+8^2} ⇒ D =
sqrt{144 + 64} ⇒ D = √208
⇒ D = 4√3
Vraag 3. Zoek de oppervlakte van een ruit met de twee diagonale lengtes d 1 en d 2 respectievelijk 6 cm en 12 cm zijn.
Oplossing:
We hebben,
Diagonaal d1= 6 cm
Diagonaal d2= 12 cm
De oppervlakte van de ruit wordt gegeven door,
EEN =
frac{(d_1 imes d_2)}{2} vierkante eenhedenEEN =
frac{( 6 imes 12)}{2} EEN =
frac{72}{2} A = 36 cm2
Daarom is de oppervlakte van de ruit = 36 cm2.
Vraag 4. Verschil tussen ruit en rechthoek?
Oplossing:
| Eigendom | Ruit | Rechthoek |
| Zijkanten | Gelijke kanten. | Overstaande zijden zijn gelijk. |
| Diagonalen | De diagonalen snijden elkaar in een hoek van 90°. Diagonalen maken rechte hoeken in het midden. | De diagonalen snijden elkaar onder verschillende hoeken. De ene hoek is een stompe hoek en de andere een scherpe hoek. Diagonalen maken in het midden verschillende hoeken: een stompe hoek en een scherpe hoek. |
| Hoeken | Tegenovergestelde hoeken zijn gelijk. Aangrenzende hoeken bedragen samen 180°. | Tegengestelde en aangrenzende hoeken zijn gelijk. Een hoek gevormd door de aangrenzende zijden van een rechthoek is 90°. |
