A Gerichte acyclische grafiek , vaak afgekort als DAG , is een fundamenteel concept in de grafentheorie. DAG's worden gebruikt om op een duidelijke en georganiseerde manier te laten zien hoe dingen met elkaar verband houden of van elkaar afhankelijk zijn. In dit artikel gaan we er meer over leren Gerichte acyclische grafiek , de eigenschappen ervan en de toepassing in het echte leven.

Gerichte acyclische grafiek

Wat is een gerichte acyclische grafiek?

A Gerichte acyclische grafiek (DAG) is een gerichte graaf die geen cycli bevat.

Onderstaande grafiek vertegenwoordigt een gerichte acyclische grafiek (DAG):

Directe acyclische grafiek

Betekenis van gerichte acyclische grafiek:

Gerichte acyclische grafiek heeft twee belangrijke kenmerken:

• Gerichte rand S:In gerichte acyclische grafiek, elke rand heeft een richting, wat betekent dat deze van het ene hoekpunt (knooppunt) naar het andere gaat. Deze richting betekent a een manier relatie of afhankelijkheid tussen knooppunten.
• Acyclisch: De voorwaarde acyclisch geeft aan dat er geen cycli of gesloten lussen in de grafiek voorkomen. Met andere woorden, u kunt niet een reeks gerichte randen doorlopen en terugkeren naar hetzelfde knooppunt, waarbij u de randrichtingen volgt. Het vormen van cycli is verboden in DAG. Daarom is dit kenmerk essentieel.

Gerichte acyclische grafiek

Eigenschappen van gerichte acyclische grafiek DAG:

Directed Acyclic Graph (DAG) heeft verschillende eigenschappen waardoor ze bruikbaar zijn bij grafiekproblemen.

Er zijn de volgende eigenschappen van Directed Acyclic Graph (DAG):

• Bereikbaarheidsrelatie: In DAG kunnen we bepalen of er een bereikbaarheidsrelatie bestaat tussen twee knooppunten. Er wordt gezegd dat knooppunt A bereikbaar is vanaf knooppunt B als er een gericht pad bestaat dat begint bij knooppunt B en eindigt bij knooppunt A. Dit houdt in dat je de richting van de randen in de grafiek kunt volgen om van B naar A te komen.
• Transitieve sluiting: De transitieve afsluiting van een gerichte graaf is een nieuwe graaf die alle directe en indirecte relaties of verbindingen tussen knooppunten in de oorspronkelijke graaf weergeeft. Met andere woorden, het vertelt u welke knooppunten vanuit andere knooppunten kunnen worden bereikt door een of meer gerichte randen te volgen.

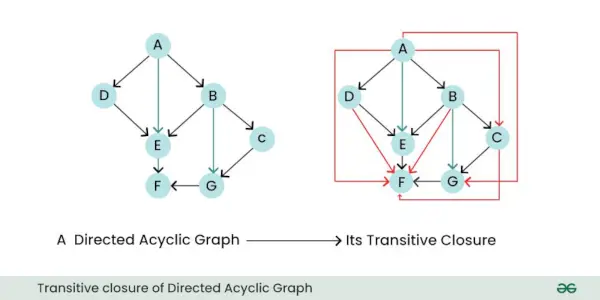
Transitieve sluiting van gerichte acyclische grafiek

• Transitieve reductie: De transitieve reductie van een gerichte graaf is een nieuwe graaf die alleen de essentiële, directe relaties tussen knooppunten behoudt, terwijl alle onnodige indirecte randen worden verwijderd. In wezen vereenvoudigt het de grafiek door randen te elimineren die kunnen worden afgeleid uit de resterende randen.

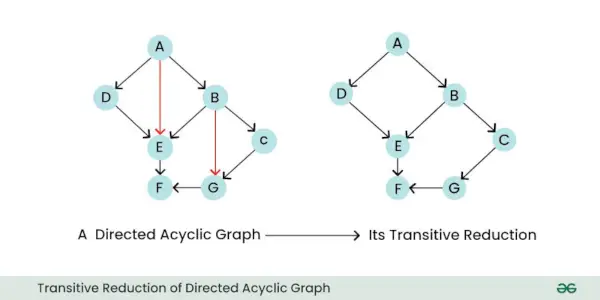
Transitieve reductie van gerichte acyclische grafiek

• Topologische ordening: Een DAG kan topologisch worden gesorteerd, wat betekent dat je de knooppunten lineair zo kunt ordenen dat voor alle randen het startknooppunt van de rand eerder in de reeks voorkomt. Deze eigenschap is handig voor taken zoals planning en het oplossen van afhankelijkheid.

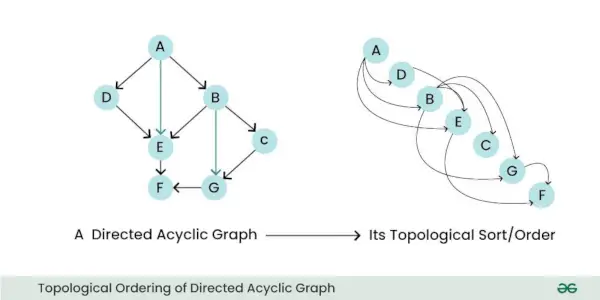
Topologische ordening van gerichte acyclische grafiek

Praktische toepassingen van DAG:

• Gegevensstroomanalyse: Bij het ontwerp en de optimalisatie van compilers worden DAG's gebruikt om de gegevensstroom binnen een programma weer te geven. Dit helpt bij het optimaliseren van code door overtollige berekeningen en dode code te identificeren. DAG's worden ook gebruikt om de structuur van basis blokken in compilerontwerp.

• Taakplanning: DAG's worden gebruikt bij projectbeheer en taakplanning. Elke taak of taak wordt weergegeven als een knooppunt in de DAG, waarbij gerichte randen de afhankelijkheden aangeven. Het acyclische karakter van de DAG zorgt ervoor dat taken in een logische volgorde worden gepland, waardoor circulaire afhankelijkheden worden voorkomen.

Een gewogen gerichte acyclische grafiek kan worden gebruikt om een ​​planningsprobleem weer te geven. Laten we het voorbeeld nemen van een taakplanningsprobleem. Hier kan een hoekpunt de taak vertegenwoordigen en het gewicht ervan kan de omvang van de taakberekening vertegenwoordigen. Op dezelfde manier kan een rand de communicatie tussen twee taken vertegenwoordigen en kan het gewicht ervan de communicatiekosten vertegenwoordigen:

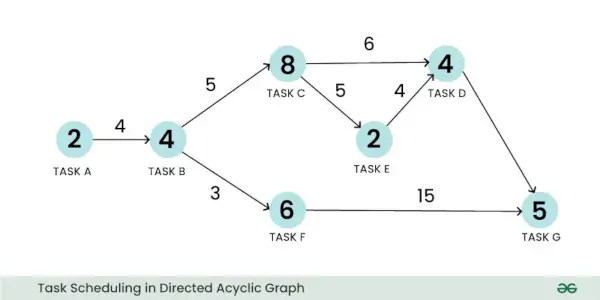
Taakplanning in gerichte acyclische grafiek

Conclusie:

Samenvattend zijn gerichte acyclische grafieken een fundamenteel concept van de grafentheorie met talrijke praktische toepassingen. DAG's spelen een cruciale rol bij taakplanning, gegevensstroomanalyse, afhankelijkheidsresolutie en verschillende andere gebieden van informatica en techniek. Ze helpen processen te optimaliseren, afhankelijkheden te beheren en een efficiënte uitvoering van taken of klussen te garanderen.