De formule Hoogte van een parallellogram is bedoeld om de hoogte van een parallellogram te berekenen. De hoogte van een parallellogram is de loodrechte afstand tussen de basiszijde en de parallelle zijde er tegenover. Een parallellogram kan worden gedefinieerd als een vierhoek waarin tegenoverliggende zijden evenwijdig zijn en de lengte van deze tegenoverliggende zijden ook gelijk is.

Hoogte van een parallellogramformule

De tegenovergestelde hoeken van het parallellogram zijn ook gelijk. Laten we hieronder meer weten over de hoogte van een parallellogramformule met afleiding.

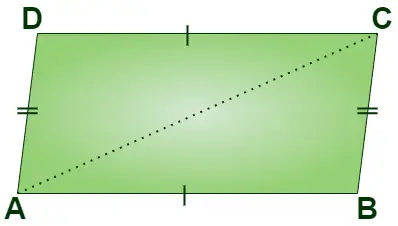
Hoogte van een parallellogramformule

Hoogte van een parallellogramformule

De hoogte van een parallellogram wordt berekend met behulp van de formule Oppervlakte is gelijk aan Basis vermenigvuldigd met Hoogte, dus als de oppervlakte van a Parallellogram Het is bekend dat de hoogte wordt berekend door het gebied te delen door de basis.

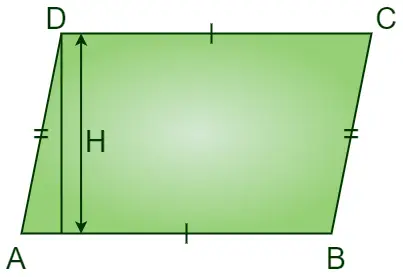
De hoogte van een parallellogramformule wordt afgeleid van de oppervlakteformule, oppervlakte van een parallellogram kan worden gevonden met behulp van de basislengte en hoogte van het parallellogram.

Oppervlakte = Basis × Hoogte

Hoogte = Oppervlakte/basis

Omtrek van een parallellogram

Omtrek wordt gedefinieerd als de som van alle zijden waarmee een gesloten figuur wordt geconstrueerd. In het geval van een parallellogram heeft het vier zijden waarvan de tegenoverliggende zijden gelijk zijn, dus de omtrek is de som van alle vier de zijden.

Laten we de maat nemen van tegenoverliggende zijden als X en Y

Omtrek van parallellogram = X + Y + X + Y = 2X + 2Y = 2(X + Y)

Omtrek = 2(X + Y)

Gerelateerde bronnen

• Parallelle lijnen
• Gebied van rechthoek
• Omtrek van rechthoek

Opgelost voorbeeld van de hoogte van het parallellogram

Voorbeeld 1: Vind de hoogte van een parallellogram als de oppervlakte 625 cm is ² en de lengte van de voet is 25 cm.

Oplossing:

De hoogte van een parallellogram kan worden berekend met behulp van de hoogte van een parallellogramformule

Hoogte = Oppervlakte / Basis

Hoogte = 625/25

Hoogte = 25 cm.

De hoogte van het parallellogram is dus 25 cm

Voorbeeld 2: Zoek de oppervlakte van een parallellogram waarvan de basis 20 cm is en de hoogte 15 cm.

Oplossing:

Gebied van parallellogram = basis x hoogte

Basis en hoogte zijn respectievelijk 20 cm en 15 cm.

Oppervlakte = 20 × 15

Oppervlakte = 300 cm.

Voorbeeld 3: De omtrek van een parallellogram is 226 cm en één zijde van het parallellogram heeft een lengte van 12 cm, bereken de maat van de andere zijde.

Oplossing:

Java8-functies

Omtrek van parallellogram = 2(X + Y)

Waar X de lengte van de ene zijde is en Y de lengte van de andere zijde, dus laat X = 12 cm

226 = 2(X+Y)

2(X+Y) = 226

2(12 + J) = 226

24 + 2Y =226

2J = 226 – 24

2J = 202

J = 202/2

Y = 101 cm.

Voorbeeld 4: Vind de hoogte van een parallellogram als de oppervlakte 800 cm is ² en de lengte van de voet is 40 cm.

Oplossing

De hoogte van een parallellogram kan worden berekend met behulp van de hoogte van een parallellogramformule

Hoogte = Oppervlakte / Basis

Hoogte = 800/40

Hoogte = 20 cm.

De hoogte van het parallellogram is dus 20 cm

Voorbeeld 5: De omtrek van een parallellogram is 400 cm en één zijde van het parallellogram heeft een lengte van 80 cm. Bereken de maat van een andere zijde.

Oplossing:

Omtrek van parallellogram = 2(X + Y)

Waar X de lengte van de ene zijde is en Y de lengte van de andere zijde, dus laat X = 80 cm

400 = 2(X+Y)

java toevoegen aan een array

2(X+Y) = 400

2(80 + J) = 400

160 + 2J =400

2J = 400 – 160

2J = 240

Y = 120cm.

Hoogte van parallellogramformule

Wat is de formule voor de hoogte van het parallellogram?

De formule voor de hoogte van het parallellogram is oppervlakte(a)/basis(b).

Wat is de basis en de hoogte van een parallellogram?

Basis verwijst naar de lengte van een zijde en Hoogte is de lengte van een loodlijn tussen twee parallelle lijnen.

Wat is de hoogte van een parallellogram?

De hoogte van een parallellogram wordt de loodrechte afstand tussen twee parallelle lijnen van een parallellogram genoemd.

Wat is de oppervlakte van een parallellogram?

Het gebied van het parallellogram wordt de ruimte binnen de grens van een parallellogram genoemd.