De hoogte of diepte van een binaire boom kan worden gedefinieerd als het maximale of het grootste aantal randen van een bladknooppunt naar het wortelknooppunt of het wortelknooppunt naar het bladknooppunt. Het hoofdknooppunt bevindt zich op niveau nul, wat betekent dat als op het hoofdknooppunt geen van de onderliggende knooppunten is aangesloten, de hoogte of diepte van de specifieke binaire boom nul is.
Laten we een voorbeeld nemen voor een beter begrip van de hoogte van de binaire boom.
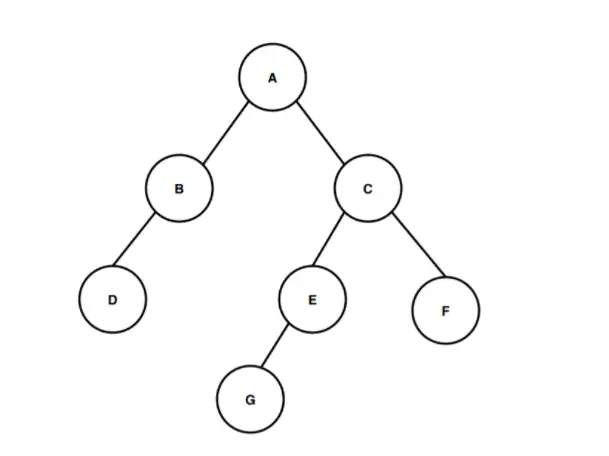
In de bovenstaande afbeelding hebben we een binaire boom die begint bij het hoofdknooppunt met de naam A. Het hoofdknooppunt A heeft twee onderliggende knooppunten B en C als respectievelijk het linkerkind en het rechterkind. En op dezelfde manier heeft het linkerkindknooppunt B slechts één linkerkindknooppunt genaamd D en het rechterkindknooppunt C heeft twee kindknooppunten E en F, waarvan knooppunt E knooppunt G heeft als het enige linkerkind.
robotcomponenten
Laten we nu de hoogte van deze binaire boom berekenen. Tel het aantal randen vanaf het wortelknooppunt tot het diepste bladknooppunt om de hoogte van de binaire boom te berekenen. Het diepste knooppunt dat in deze binaire boom aanwezig is, is knooppunt G. Voor de berekening van de hoogte of diepte van deze binaire boom moeten we dus het aantal randen berekenen tussen het hoofdknooppunt en het diepste knooppunt G. De eerste rand loopt van knooppunt A naar knooppunt C, de tweede rand loopt van knooppunt C naar knooppunt E en de derde rand loopt van knooppunt E naar knooppunt G. Dus als u van het hoofdknooppunt A naar het diepste knooppunt G gaat, zijn er drie randen , dus de hoogte of diepte van de binaire boom is 3. Het pad dat we hebben gevolgd om van de wortel naar het diepste bladknooppunt te gaan is A > C > E > G en dit pad beslaat drie randen tijdens de doorgang, daarom volgens volgens de definitie van de hoogte van de binaire boom is de hoogte van deze binaire boom 3.
Manieren om de hoogte van de binaire boom te vinden
Laten we nu code schrijven om de hoogte van een binaire boom te vinden. Er zijn twee manieren om de hoogte van de binaire boom te vinden. Eén is de recursieve methode en de andere is de niet-recursieve methode dat gebruik zal maken van de wachtrijgegevensstructuur om de hoogte van de binaire boom te berekenen.
Recursieve manier
Laten we eerst eens kijken naar de recursieve manier om de hoogte van de binaire boom te vinden.
Code:
// Java program to create and to find the height of a binary tree by recursive way // util package is imported to use classes like Queue and LinkedList import java.util.*; // A class named Node is created representing a single node of a binary tree class Node{ // The class Node has three class variables named key and left and right of int type and Node type respectively. // the key variable holds the actual value that is assigned to that node of the binary tree int key; // left and right variables that are of Node type will be used to store the left and right child nodes of the parent of the binary tree Node left, right; // a parameterized constructor is created to create and add data to the node at the same time. public Node(int item) { key = item; left = right = null; } } // end of node class definition // A public class named BinaryTree is created having two constructors and methods to print the binary tree level-wise. class BinaryTree{ // A static variable named root_node is created that will represent the node of the binary tree static Node root_node; // A parametrized constructor of the BinaryTree class is written having the key as a parameter BinaryTree(int key) { // here we are constructing a new node and assigning it to the root node root_node = new Node(key); } BinaryTree() { root_node = null; } // a public static function named print tree is created to print all the nodes in the tree level-wise starting from the root node public static void printTree() { int h = height(root_node); int i; for (i=1; i<=h; i++){ printcurrentlevel(root_node, i); system.out.println(); } a public static function named height is created to fund the of binary tree starting from root node deepest leaf that present in passed as parameter called recursively until returned null find int height(node root){ then will be zero if (root="=" null) return 0; else { * compute each subtree lheight="height(root.left);" rheight="height(root.right);" use larger one both sub trees calcualted and which higher used. (lheight> rheight) return(lheight+1); else return(rheight+1); } } // a Public static function named printCurrentLevel is created to print al the nodes that are present in that level // this function is called repeatedly for each level of the binary tree to print all the nodes in that particular level public static void printCurrentLevel (Node root ,int level) { if (root == null) return; if (level == 1) System.out.print(root.key + ' '); else if (level > 1) { printCurrentLevel(root.left, level-1); printCurrentLevel(root.right, level-1); } } //the main function is created to create an object of the BinaryTree class and call the printTree method to level-wise print the nodes of the binary tree and the height method to find the height of the binary tree public static void main(String[] args){ // first of all we have created an Object of the BinaryTree class that will represent the binary tree BinaryTree tree = new BinaryTree(); // now a new node with the value as 150 is added as the root node to the Binary Tree tree.root_node = new Node(150); // now a new node with the value 250 is added as a left child to the root node tree.root_node.left = new Node(250); // now a new node with the value 270 is added as a right child to the root node tree.root_node.right = new Node(270); // now a new node with the value 320 is added as a left child to the left node of the previous level node tree.root_node.left.left = new Node(320); // now a new node with the value 350 is added as a right child to the right node of the previous level node tree.root_node.left.right = new Node(350); /* 150 / 250 270 / / 320 350 null null */ System.out.println('Printing the nodes of tree level wise :'); System.out.println('Level order traversal : '); tree.printTree(); // height of the binary tree is calculated bypassing the root as parameter to the height() function. int h = tree.height(tree.root_node) System.out.println('The height of the Binary tree is : ' + h ); } } // end of the BinaryTree class </=h;> Uitgang: De uitvoer van de bovenstaande code is:
Printing the nodes of tree level wise: Level order traversal: (level 0) 150 (level 1) 250 270 (level 2) 320 350 The height of the Binary tree is: 2
Op recursieve wijze hebben we de hoogte() functie herhaaldelijk om de hoogte van de binaire boom te vinden. Het hoofdknooppunt van de binaire boom wordt als parameter doorgegeven aan de functie height(). De functie height() berekent de hoogte van beide subbomen van het hoofdknooppunt en welke van beide hoogten hoger is, wordt beschouwd als de hoogte van de binaire boom.
abstracte klasse
Niet-recursieve manier
Laten we nu eens kijken naar de niet-recursieve manier om de hoogte van de binaire boom te vinden.
Code:
// A C++ program to create and to find the height of a binary tree by non recursive way // iostream header file is included to use the cin and cout objects of the istream and ostream classes respectively #include #include using namespace std; // A struct named Node is created representing a single node of a binary tree struct Node { // The struct Node has three variables named key and left and right of int type and Node type respectively. // the key variable holds the actual value that is assigned to that node of the binary tree int key; // left and right variables that are of Node type will be used to store the left and right child nodes of the parent of the binary tree struct Node* left, *right; }; // A Function named newNode is created to add a new node to the binary tree, the newNode function has one parameter of integer type named key that will represent the value that particular new node will be storing Node* newNode(int key) { Node* temp = new Node; temp->key = key; temp->left = temp->right = NULL; return (temp); } // A function named height is created to find the height of the binary tree with non recursive way // The parameter to the height function is the root node of the binary tree that will be present at level zero // In the height function the nodes of the binary tree are added into the Queue data structure and the depth variable is incremented until // the NULL node is encountered while traversing the nodes of the binary tree stored in the Queue data structure. int height(struct Node* root){ //Initialising a variable to count the //height of tree int depth = 0; queueq; //Pushing first level element along with NULL q.push(root); q.push(NULL); while(!q.empty()){ Node* temp = q.front(); q.pop(); //When NULL encountered, increment the value if(temp == NULL){ depth++; } //If NULL not encountered, keep moving if(temp != NULL){ if(temp->left){ q.push(temp->left); } if(temp->right){ q.push(temp->right); } } //If queue still have elements left, //push NULL again to the queue. else if(!q.empty()){ q.push(NULL); } } return depth; } // Start of the main function int main() { // first of all we have created an Object of the struct Node that will represent the binary tree // the value of the root node is 10 Node *root = newNode(10); // now a new node with the value 20 is added as a left child to the root node root->left = newNode(20); // now a new node with the value 30 is added as a right child to the root node root->right = newNode(30); // now a new node with the value 40 is added as a left child to the left node of the previous level node root->left->left = newNode(40); // now a new node with the value 50 is added as a right child to the left node of the previous level node root->left->right = newNode(50); /* 10 / 20 30 / / 40 50 null null */ cout<<'the height(depth) of tree is: '<<height(root); cout<<endl; } end the main function < pre> <p> <strong>Output:</strong> </p> <pre> The Height(Depth) of the tree is: 2 </pre> <p>In this approach, we have used a non recursive way to find the depth of the binary tree. To find the height of the binary tree, we have written a function named height that will require a parameter of Node type (that means the root of the binary tree whose height needs to be calculated). The root of the binary tree is present at level zero, which means the height or depth of the root is zero.</p> <p>In the non recursive approach, we use the Queue Data Structure to find the depth of the binary tree. The nodes of the binary tree for which we want to find the depth are added to the Queue data structure with the help of an enqueue operation to which the node of the binary tree is passed as a parameter to this function.</p> <p>Once all the nodes are added to the queue, the nodes added in the queue are removed by calling the dequeue function that will keep on removing one element from the queue until the null node of the binary tree is encountered. Each time a node of the binary tree from the queue is removed, the depth variable representing the depth of the binary tree is incremented by one. And in the end, the value of the depth variable will represent the final depth of the binary tree.</p> <hr></'the> Bij deze benadering hebben we een niet-recursieve manier gebruikt om de diepte van de binaire boom te vinden. Om de hoogte van de binaire boom te vinden, hebben we een functie geschreven met de naam height waarvoor een parameter van het knooppunttype nodig is (dat wil zeggen de wortel van de binaire boom waarvan de hoogte moet worden berekend). De wortel van de binaire boom bevindt zich op niveau nul, wat betekent dat de hoogte of diepte van de wortel nul is.
Bij de niet-recursieve benadering gebruiken we de wachtrijgegevensstructuur om de diepte van de binaire boom te vinden. De knooppunten van de binaire boom waarvan we de diepte willen vinden, worden aan de wachtrijgegevensstructuur toegevoegd met behulp van een wachtrijbewerking waaraan het knooppunt van de binaire boom als parameter aan deze functie wordt doorgegeven.
Zodra alle knooppunten aan de wachtrij zijn toegevoegd, worden de aan de wachtrij toegevoegde knooppunten verwijderd door de dequeue-functie aan te roepen die één element uit de wachtrij blijft verwijderen totdat het nulknooppunt van de binaire boom wordt aangetroffen. Elke keer dat een knooppunt van de binaire boom uit de wachtrij wordt verwijderd, wordt de dieptevariabele die de diepte van de binaire boom vertegenwoordigt, met één verhoogd. En uiteindelijk zal de waarde van de dieptevariabele de uiteindelijke diepte van de binaire boom vertegenwoordigen.
