In Java is Heap een speciaal type gegevensstructuur waarbij het hoofdknooppunt of het bovenliggende knooppunt wordt vergeleken met de linker- en rechterkinderen en in volgorde wordt gerangschikt. Stel dat x een hoofdknooppunt is en y het onderliggende knooppunt, eigenschap sleutel(x)<= key(y)< strong>zal min-heap genereren, en naar die relatie wordt verwezen als 'Heap-eigendom' .
Op basis van de volgorde van de bovenliggende en onderliggende knooppunten kan Heap in twee vormen worden geclassificeerd, namelijk Min heap en Max heap. Laten we ze allebei een voor een begrijpen en de code in Java implementeren.
Min hoop
Min heap is een speciaal type heap-gegevensstructuur die op zichzelf een complete binaire boom is. Min heap heeft de volgende eigenschappen:
- De waarde van het hoofdknooppunt is altijd kleiner in vergelijking met de andere knooppunten van de heap.
- Elk intern knooppunt heeft een sleutelwaarde die altijd kleiner is dan of gelijk is aan de onderliggende knooppunten.
We kunnen de volgende drie bewerkingen uitvoeren in Min heap:
insertNode()
We kunnen het invoegen in de Min-heap uitvoeren door een nieuwe sleutel aan het einde van de boom toe te voegen. Als de waarde van de ingevoegde sleutel kleiner is dan het bovenliggende knooppunt, moeten we de sleutel naar boven doorlopen om aan de heap-eigenschap te voldoen. Het invoegproces kost O(log n) tijd.
extractMin()
Het is een van de belangrijkste bewerkingen die we uitvoeren om het knooppunt met de minimumwaarde te verwijderen, dat wil zeggen het hoofdknooppunt van de heap. Na het verwijderen van het rootknooppunt moeten we ervoor zorgen dat de heap-eigenschap behouden blijft. De bewerking extractMin() kost O(Logn) tijd om het minimumelement uit de heap te verwijderen.
Hoe te converteren van string naar int
getMin()
De getMin() bewerking wordt gebruikt om het hoofdknooppunt van de heap te verkrijgen, dat wil zeggen het minimale element in O(1) tijd.
Voorbeeld:
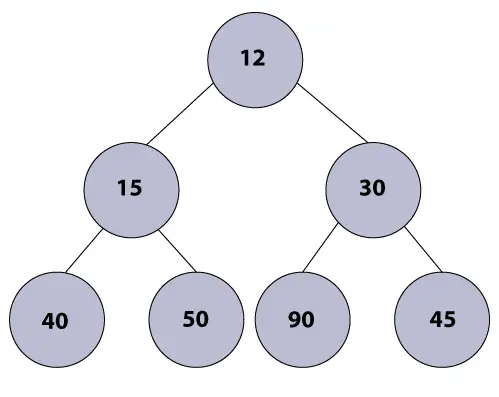
Min heap-algoritme
proceduredesign_min_heap Array arr: of size n => array of elements // call min_heapify procedure for each element of the array to form min heap repeat for (k = n/2 ; k >= 1 ; k--) call procedure min_heapify (arr, k); proceduremin_heapify (vararr[ ] , var k, varn) { varleft_child = 2*k; varright_child = 2*k+1; var smallest; if(left_child<= n and arr[left_child ] <arr[ k ) smallest="left_child;" else if(right_child<="n" arr[right_child <arr[smallest] if(smallest !="k)" { swaparr[ arr[ ]); callmin_heapify (arr, smallest, n); } < pre> <p> <strong>MinHeapJavaImplementation.java</strong> </p> <pre> // import required classes and packages packagejavaTpoint.javacodes; importjava.util.Scanner; // create class MinHeap to construct Min heap in Java classMinHeap { // declare array and variables privateint[] heapData; privateintsizeOfHeap; privateintheapMaxSize; private static final int FRONT = 1; //use constructor to initialize heapData array publicMinHeap(intheapMaxSize) { this.heapMaxSize = heapMaxSize; this.sizeOfHeap = 0; heapData = new int[this.heapMaxSize + 1]; heapData[0] = Integer.MIN_VALUE; } // create getParentPos() method that returns parent position for the node privateintgetParentPosition(int position) { return position / 2; } // create getLeftChildPosition() method that returns the position of left child privateintgetLeftChildPosition(int position) { return (2 * position); } // create getRightChildPosition() method that returns the position of right child privateintgetRightChildPosition(int position) { return (2 * position) + 1; } // checks whether the given node is leaf or not privatebooleancheckLeaf(int position) { if (position >= (sizeOfHeap / 2) && position heapData[getLeftChildPosition(position)] || heapData[position] >heapData[getRightChildPosition(position)]) { // swap with left child and then heapify the left child if (heapData[getLeftChildPosition(position)] = heapMaxSize) { return; } heapData[++sizeOfHeap] = data; int current = sizeOfHeap; while (heapData[current] <heapdata[getparentposition(current)]) { swap(current, getparentposition(current)); current="getParentPosition(current);" } crreatedisplayheap() method to print the data of heap public void displayheap() system.out.println('parent node' + ' ' 'left child 'right node'); for (int k="1;" position--) minheapify(position); create removeroot() removing minimum element from publicintremoveroot() intpopelement="heapData[FRONT];" heapdata[front]="heapData[sizeOfHeap--];" minheapify(front); returnpopelement; minheapjavaimplementation class in java classminheapjavaimplementation{ main() start static main(string[] arg) declare variable intheapsize; scanner object sc="new" scanner(system.in); system.out.println('enter size min heap'); heapsize="sc.nextInt();" minheapheapobj="new" minheap(heapsize); for(inti="1;" i<="heapSize;" i++) system.out.print('enter '+i+' element: '); int heapobj.insertnode(data); close obj sc.close(); construct a given heapobj.designminheap(); display system.out.println('the is heapobj.displayheap(); root node system.out.println('after element(root node) '+heapobj.removeroot()+', is:'); < pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/java-tutorial/97/heap-implementation-java-2.webp" alt="Heap implementation in Java"> <h2>Max heap</h2> <p>Max heap is another special type of heap data structure that is also a complete binary tree in itself in Java. Max heap has the following properties:</p> <ol class="points"> <li>Root node value is always greater in comparison to the other nodes of the heap.</li> <li>Each internal node has a key value that is always greater or equal to its children.</li> </ol> <p>We can perform the following three operations in Max heap:</p> <h3>insertNode()</h3> <p>We can perform insertion in the Max heap by adding a new key at the end of the tree. If the value of the inserted key is greater than its parent node, we have to traverse the key upwards for fulfilling the heap property. The insertion process takes O(log n) time.</p> <h3>extractMax()</h3> <p>It is one of the most important operations which we perform to remove the maximum value node, i.e., the root node of the heap. After removing the root node, we have to make sure that heap property should be maintained. The extractMax() operation takes O(Log n) time to remove the maximum element from the heap.</p> <h3>getMax()</h3> <p>The <strong>getMax()</strong> operation is used to get the root node of the heap, i.e., maximum element in O(1) time.</p> <p> <strong>Example:</strong> </p> <img src="//techcodeview.com/img/java-tutorial/97/heap-implementation-java-3.webp" alt="Heap implementation in Java"> <p> <strong>Min heap Algorithm</strong> </p> <pre> proceduredesign_max_heap Array arr: of size n => array of elements // call min_heapify procedure for each element of the array to form max heap repeat for (k = n/2 ; k >= 1 ; k--) call procedure max_heapify (arr, k); proceduremin_heapify (vararr[ ] , var k, varn) { varleft_child = 2*k + 1; varright_child = 2*k+ 2; if(left_childarr[ largest ] ) largest = left_child; else largest = k; if(right_childarr[largest] ) largest = right_child; if(largest != k) { swaparr[ k ] and arr[ largest ]); callmax_heapify (arr, largest, n); } } </pre> <p> <strong>MaxHeapJavaImplementation.java</strong> </p> <pre> //import required classes and packages packagejavaTpoint.javacodes; importjava.util.Scanner; //create class MinHeap to construct Min heap in Java classMaxHeap { // declare array and variables privateint[] heapData; privateintsizeOfHeap; privateintheapMaxSize; private static final int FRONT = 1; //use constructor to initialize heapData array publicMaxHeap(intheapMaxSize) { this.heapMaxSize = heapMaxSize; this.sizeOfHeap = 0; heapData = new int[this.heapMaxSize]; } // create getParentPos() method that returns parent position for the node privateintgetParentPosition(int position) { return (position - 1) / 2; } // create getLeftChildPosition() method that returns the position of left child privateintgetLeftChildPosition(int position) { return (2 * position); } // create getRightChildPosition() method that returns the position of right child privateintgetRightChildPosition(int position) { return (2 * position) + 1; } // checks whether the given node is leaf or not privatebooleancheckLeaf(int position) { if (position > (sizeOfHeap / 2) && position <= sizeofheap) { return true; } false; create swapnodes() method that perform swapping of the given nodes heap firstnode and secondnode are positions private void swap(intfirstnode, intsecondnode) int temp; temp="heapData[firstNode];" heapdata[firstnode]="heapData[secondNode];" heapdata[secondnode]="temp;" maxheapify() to heapify node for maintaining property maxheapify(int position) check whether is non-leaf greater than its right left child if (!checkleaf(position)) (heapdata[position] <heapdata[getleftchildposition(position)] || heapdata[position] heapdata[getrightchildposition(position)]) swap(position, getleftchildposition(position)); maxheapify(getleftchildposition(position)); swap with else getrightchildposition(position)); maxheapify(getrightchildposition(position)); insertnode() insert element in public insertnode(int data) heapdata[sizeofheap]="data;" current="sizeOfHeap;" while (heapdata[current]>heapData[getParentPosition(current)]) { swap(current, getParentPosition(current)); current = getParentPosition(current); } sizeOfHeap++; } // create displayHeap() method to print the data of the heap public void displayHeap() { System.out.println('PARENT NODE' + ' ' + 'LEFT CHILD NODE' + ' ' + 'RIGHT CHILD NODE'); for (int k = 0; k <sizeofheap 2; k++) { system.out.print(' ' + heapdata[k] ' ' heapdata[2 * k 1] 2]); system.out.println(); } create designmaxheap() method to construct min heap public void for (int position="0;" < (sizeofheap 2); position++) maxheapify(position); removeroot() removing maximum element from the publicintremoveroot() intpopelement="heapData[FRONT];" heapdata[front]="heapData[sizeOfHeap--];" maxheapify(front); returnpopelement; minheapjavaimplementation class in java classmaxheapjavaimplementation{ main() start static main(string[] arg) declare variable intheapsize; scanner object sc="new" scanner(system.in); system.out.println('enter size of max heap'); heapsize="sc.nextInt();" maxheapheapobj="new" maxheap(50); for(inti="1;" i<="heapSize;" i++) system.out.print('enter '+i+' element: '); int data="sc.nextInt();" heapobj.insertnode(data); close obj sc.close(); a given heapobj.designmaxheap(); display system.out.println('the is heapobj.displayheap(); root node system.out.println('after element(root node) '+heapobj.removeroot()+', is:'); pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/java-tutorial/97/heap-implementation-java-4.webp" alt="Heap implementation in Java"> <hr></sizeofheap></=></pre></heapdata[getparentposition(current)])></pre></=> MaxHeapJavaImplementation.java
//import required classes and packages packagejavaTpoint.javacodes; importjava.util.Scanner; //create class MinHeap to construct Min heap in Java classMaxHeap { // declare array and variables privateint[] heapData; privateintsizeOfHeap; privateintheapMaxSize; private static final int FRONT = 1; //use constructor to initialize heapData array publicMaxHeap(intheapMaxSize) { this.heapMaxSize = heapMaxSize; this.sizeOfHeap = 0; heapData = new int[this.heapMaxSize]; } // create getParentPos() method that returns parent position for the node privateintgetParentPosition(int position) { return (position - 1) / 2; } // create getLeftChildPosition() method that returns the position of left child privateintgetLeftChildPosition(int position) { return (2 * position); } // create getRightChildPosition() method that returns the position of right child privateintgetRightChildPosition(int position) { return (2 * position) + 1; } // checks whether the given node is leaf or not privatebooleancheckLeaf(int position) { if (position > (sizeOfHeap / 2) && position <= sizeofheap) { return true; } false; create swapnodes() method that perform swapping of the given nodes heap firstnode and secondnode are positions private void swap(intfirstnode, intsecondnode) int temp; temp="heapData[firstNode];" heapdata[firstnode]="heapData[secondNode];" heapdata[secondnode]="temp;" maxheapify() to heapify node for maintaining property maxheapify(int position) check whether is non-leaf greater than its right left child if (!checkleaf(position)) (heapdata[position] <heapdata[getleftchildposition(position)] || heapdata[position] heapdata[getrightchildposition(position)]) swap(position, getleftchildposition(position)); maxheapify(getleftchildposition(position)); swap with else getrightchildposition(position)); maxheapify(getrightchildposition(position)); insertnode() insert element in public insertnode(int data) heapdata[sizeofheap]="data;" current="sizeOfHeap;" while (heapdata[current]>heapData[getParentPosition(current)]) { swap(current, getParentPosition(current)); current = getParentPosition(current); } sizeOfHeap++; } // create displayHeap() method to print the data of the heap public void displayHeap() { System.out.println('PARENT NODE' + ' ' + 'LEFT CHILD NODE' + ' ' + 'RIGHT CHILD NODE'); for (int k = 0; k <sizeofheap 2; k++) { system.out.print(\' \' + heapdata[k] \' \' heapdata[2 * k 1] 2]); system.out.println(); } create designmaxheap() method to construct min heap public void for (int position="0;" < (sizeofheap 2); position++) maxheapify(position); removeroot() removing maximum element from the publicintremoveroot() intpopelement="heapData[FRONT];" heapdata[front]="heapData[sizeOfHeap--];" maxheapify(front); returnpopelement; minheapjavaimplementation class in java classmaxheapjavaimplementation{ main() start static main(string[] arg) declare variable intheapsize; scanner object sc="new" scanner(system.in); system.out.println(\'enter size of max heap\'); heapsize="sc.nextInt();" maxheapheapobj="new" maxheap(50); for(inti="1;" i<="heapSize;" i++) system.out.print(\'enter \'+i+\' element: \'); int data="sc.nextInt();" heapobj.insertnode(data); close obj sc.close(); a given heapobj.designmaxheap(); display system.out.println(\'the is heapobj.displayheap(); root node system.out.println(\'after element(root node) \'+heapobj.removeroot()+\', is:\'); pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/java-tutorial/97/heap-implementation-java-4.webp" alt="Heap implementation in Java"> <hr></sizeofheap></=>