Regressie- en probabilistische classificatieproblemen kunnen worden opgelost met behulp van het Gaussiaanse proces (GP), een begeleide leertechniek. Omdat elk Gaussiaans proces kan worden gezien als een oneindig-dimensionale generalisatie van multivariate Gaussiaanse distributies , komt de term Gaussiaans voor in de naam. We zullen Gaussiaanse processen voor regressie in dit bericht bespreken, ook wel Gaussiaanse procesregressie (GPR) genoemd. Talloze problemen uit de echte wereld op het gebied van materiaalkunde, scheikunde, natuurkunde en biologie zijn opgelost met het gebruik van GPR.
Inhoudsopgave
- Gaussiaanse procesregressie (GPR)
- Sleutelconcepten van Gaussiaanse procesregressie (GPR)
- Wiskundig concept van Gaussiaanse procesregressie (GPR)
- Implementatie van Gauss-proces in Python
Gaussiaanse procesregressie (GPR)
Gaussiaanse procesregressie (GPR) is een krachtige en flexibele niet-parametrische regressietechniek die wordt gebruikt bij machinaal leren En statistieken . Het is met name handig bij het omgaan met problemen met continue gegevens, waarbij de relatie tussen invoervariabelen en uitvoer niet expliciet bekend is of complex kan zijn. GPR is een Bayesiaanse benadering die zekerheid in voorspellingen kan modelleren, waardoor het een waardevol hulpmiddel is voor verschillende toepassingen, waaronder optimalisatie, tijdreeksvoorspellingen en meer. GPR is gebaseerd op het concept van een Gauss-proces, dat een verzameling willekeurige variabelen is, waarvan elk eindig aantal een gezamenlijke Gauss-verdeling heeft. Een Gaussiaans proces kan worden gezien als een verdeling van functies.
Sleutelconcepten van Gaussiaanse procesregressie (GPR)
Gaussain-proces
Een niet-parametrisch, probabilistisch model genaamd a Gaussiaans proces (GP) wordt gebruikt in statistieken en machinaal leren voor regressie, classificatie en kwantificering van onzekerheid. Het toont een groep willekeurige variabelen, die elk een gezamenlijke Gaussiaanse verdeling hebben en een eindig aantal kunnen hebben. Huisartsen zijn een veelzijdige en effectieve techniek voor het modelleren van ingewikkelde relaties in gegevens en het maken van voorspellingen met bijbehorende onzekerheid.
Kenmerken van Gaussische processen :
variabel globaal javascript
- Niet-parametrische aard : Huisartsen kunnen zich aanpassen aan de complexiteit van de gegevens omdat ze niet afhankelijk zijn van een vast aantal modelparameters
- Probabilistische voorspellingen : Voorspellingen van huisartsen kunnen worden gekwantificeerd omdat ze voorspellingen doen als kansverdelingen.
- Interpolatie en afvlakking : Huisartsen zijn handig voor gegevens met ruis of onregelmatig bemonsterde gegevens, omdat ze goed zijn in het gladstrijken van gegevens met ruis en het interpoleren tussen gegevenspunten.
- Marginalisering van hyperparameters : Door de vereiste voor het expliciet aanpassen van hyperparameters te elimineren, marginaliseren ze hyperparameters, waardoor het model eenvoudiger wordt.
Gemiddelde functie
De voorspelde waarde van de functie die op elk invoerpunt wordt gemodelleerd, wordt weergegeven door de gemiddelde functie in Gaussiaanse processen (huisartsen). Het fungeert als een fundamenteel vermoeden met betrekking tot de onderliggende datastructuur. De gemiddelde functie wordt vaak standaard op nul gezet, niet noodzakelijkerwijs, en kan worden gewijzigd op basis van gegevenseigenschappen of domeinexpertise. Door de centrale tendens van voorspellingen te beïnvloeden, helpt het huisartsen bij het identificeren van patronen of trends in de gegevens. Huisartsen geven probabilistische voorspellingen die zowel onzekerheid als puntschattingen bevatten door de gemiddelde functie op te nemen
Covariantie (kernel) functie
De covariantie functie , ook wel de kernelfunctie genoemd, meet hoe vergelijkbaar de invoergegevenspunten met elkaar zijn in Gaussiaanse processen (GP's). Het is essentieel bij het karakteriseren van het gedrag van het GP-model en beïnvloedt de selectie van functies uit de vorige distributie. De covariantiefunctie meet paarsgewijze overeenkomsten om de correlatie tussen functiewaarden vast te stellen. Huisartsen kunnen zich aanpassen aan een breed scala aan datapatronen, van vloeiende trends tot complexe structuren, omdat verschillende kernelfuncties verschillende soorten correlaties vastleggen. De prestaties van het model kunnen sterk worden beïnvloed door de kernelselectie.
Eerdere uitkeringen
De voorafgaande distributie , in Gaussiaanse processen (huisartsen), is ons begrip van functies voorafgaand aan de observatie van gegevens. Meestal wordt het beschreven door een covariantiefunctie (kernelfunctie) en een gemiddelde functie. Terwijl de covariantiefunctie de gelijkenis of correlatie beschrijft tussen functiewaarden op verschillende invoerpunten, codeert de gemiddelde functie onze eerdere verwachtingen. Dit wordt vooraf door huisartsen gebruikt om een verdeling over functies te creëren. Bij huisartsen kunnen priors worden geselecteerd om gegevensonzekerheid weer te geven, domeinkennis te integreren of gladheid aan te geven.
Posterieure distributies
Gaussiaanse processen’ latere distributie toont onze herziene aannames over functies na dataobservatie. Het stelt de waarschijnlijkheid van de gegevens samen, gegeven de functie en de eerdere verdeling. De posterior in GP-regressie biedt een verdeling over functies die het meest overeenkomt met de waargenomen gegevens. Door probabilistische voorspellingen en de kwantificering van onzekerheid mogelijk te maken, weerspiegelt de posterieure verdeling de wisselwerking tussen de eerdere overtuigingen die in de eerdere verdeling zijn opgeslagen en de informatie die door de gegevens wordt geleverd.
Wiskundig concept van Gaussiaanse procesregressie (GPR)
Voor regressietaken wordt een niet-parametrisch, probabilistisch machine learning-model gebruikt, genaamd Gaussiaanse procesregressie (GP). Bij het modelleren van ingewikkelde en dubbelzinnige interacties tussen invoer- en uitvoervariabelen is het een krachtig hulpmiddel. Aangenomen wordt dat een multivariate Gaussiaanse verdeling de gegevenspunten in GP-regressie oplevert, en het doel is om deze verdeling af te leiden.
Het GP-regressiemodel heeft de volgende wiskundige uitdrukking. Laten we aannemen dat x1, X2,…..,XNzijn de invoergegevenspunten, waarbij x tot reële getallen behoort (-2,-1,0,1…), (xi
Laten we aannemen dat y1, En2,……., EnNzijn de uitvoerwaarden, waarbij yibehoort tot een reëel getal (yi
Het GP-regressiemodel gaat ervan uit dat een Gaussiaans proces met een gemiddelde functie (
Vervolgens wordt op een reeks testlocaties x* de verdeling van f gegeven door:
Normaal gesproken worden kernelfuncties gebruikt om de gemiddelde functie en de covariantiefunctie te definiëren. Ter illustratie wordt de vierkante exponentiële kern die vaak wordt gebruikt beschreven als:
Waar,
k(x_{i}, x_{j}) = De kernelfunctie wordt hierdoor weergegeven en berekent de correlatie of gelijkenis tussen twee invoergegevenspunten, xien xJ.sigma^2 = De variantieparameter van de kernel is deze. Het bepaalt de schaal of verticale spreiding van de kernelfunctie. Het regelt hoe sterk de datapunten gecorreleerd zijn. Een hogeresigma^2 levert een kernelfunctie op met grotere variantie.- exp: De exponentiële functie is verantwoordelijk voor het verheffen van e tot de macht van het argument.
||x_{i} – x_{j}||^2 : Het verschil tussen de invoergegevenspunten, xien xJ, is de kwadratische Euclidische afstand. De geometrische scheiding tussen de punten in de kenmerkruimte wordt gemeten.- l2: Dit is een weergave van de lengteschaal of karakteristieke lengte van de kernel. Het regelt de snelheid waarmee de kernelfunctie verslechtert naarmate gegevenspunten verder uit elkaar liggen. Een lagere l zorgt ervoor dat de kernel sneller degradeert.
Het GP-regressiemodel past Bayesiaanse gevolgtrekking toe om de verdeling van f te bepalen die het meest waarschijnlijk de gegevens heeft opgeleverd, gegeven een reeks trainingsgegevens (x, y). Om dit te doen, moet de posterieure verdeling van f gegeven de gegevens worden berekend, die als volgt wordt gedefinieerd:
waarbij de marginale waarschijnlijkheid van de gegevens p(y|x) is, is de eerdere verdeling van f p(f), en de waarschijnlijkheid van de gegevens gegeven de functie f is (y|x,f).
Nadat het model de posterieure verdeling van f heeft geleerd, berekent het de posterieure voorspellende verdeling om voorspellingen te doen op aanvullende testpunten x*. Het kan als volgt worden gedefinieerd:
wat is structuur in datastructuur
Waar,
p(f^*|x*, y, x) = Dit toont, gegeven de trainingsgegevens y en x, de voorwaardelijke waarschijnlijkheid van de voorspelde functiewaarden f*op een nieuw invoerpunt x*Anders gezegd: het is de waarschijnlijkheidsverdeling over alle potentiële functiewaarden op de nieuwe invoerlocatie x*, afhankelijk van de waargenomen gegevens y en hun overeenkomende invoerlocaties x.int p(f^*|x^*, f)p(f|y,x)df = In dit gedeelte van de vergelijking wordt een integraal gebruikt om de voorwaardelijke waarschijnlijkheid te bepalen. De integraal omvat alle potentiële waarden van de functie f.p(f^*|x^*, f) = Dit is de voorwaardelijke kansverdeling van de verwachte functiewaarden f*bij x*, gegeven de functiewaarden f op enkele tussenliggende locaties.p(f|y,x) = Gegeven de waargenomen gegevens (y) en hun invoerlocaties (x), is dit de voorwaardelijke waarschijnlijkheidsverdeling van de functiewaarden (f).
Voor taken als onzekerheidsbewuste besluitvorming en actief leren biedt deze verdeling een maatstaf voor de onzekerheid van de voorspelling, wat nuttig kan zijn.
Stappen in Gaussiaanse procesregressie
- Gegevensverzameling : Verzamel de input-output-gegevensparen voor uw regressieprobleem.
- Kies een kernelfunctie : Selecteer een geschikte covariantiefunctie (kernel) die bij uw probleem past. De keuze van de kernel beïnvloedt de vorm van de functies die GPR kan modelleren.
- Parameteroptimalisatie : Schat de hyperparameters van de kernelfunctie door de waarschijnlijkheid van de gegevens te maximaliseren. Dit kan worden gedaan met behulp van optimalisatietechnieken zoals gradiëntafdaling.
- Voorspelling: Bij nieuwe input kunt u het getrainde GPR-model gebruiken om voorspellingen te doen. GPR biedt zowel het voorspelde gemiddelde als de bijbehorende onzekerheid (variantie).
Implementatie van Gaussiaanse procesregressie (GPR)
Python import numpy as np import matplotlib.pyplot as plt from sklearn.gaussian_process import GaussianProcessRegressor from sklearn.gaussian_process.kernels import RBF from sklearn.model_selection import train_test_split # Generate sample data np.random.seed(0) X = np.sort(5 * np.random.rand(80, 1), axis=0) y = np.sin(X).ravel() # Add noise to the data y += 0.1 * np.random.randn(80) # Define the kernel (RBF kernel) kernel = 1.0 * RBF(length_scale=1.0) # Create a Gaussian Process Regressor with the defined kernel gp = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=10) # Split the data into training and testing sets X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.5, random_state=0) # Fit the Gaussian Process model to the training data gp.fit(X_train, y_train) # Make predictions on the test data y_pred, sigma = gp.predict(X_test, return_std=True) # Visualize the results x = np.linspace(0, 5, 1000)[:, np.newaxis] y_mean, y_cov = gp.predict(x, return_cov=True) plt.figure(figsize=(10, 5)) plt.scatter(X_train, y_train, c='r', label='Training Data') plt.plot(x, y_mean, 'k', lw=2, zorder=9, label='Predicted Mean') plt.fill_between(x[:, 0], y_mean - 1.96 * np.sqrt(np.diag(y_cov)), y_mean + 1.96 * np.sqrt(np.diag(y_cov)), alpha=0.2, color='k', label='95% Confidence Interval') plt.xlabel('X') plt.ylabel('y') plt.legend() plt.show()> Uitgang:
Genereer in deze code eerst enkele voorbeeldgegevenspunten met toegevoegde ruis, definieer vervolgens een RBF-kernel en maak een Gaussiaanse procesregressor ermee. Het model wordt getraind op de trainingsgegevens en gebruikt om voorspellingen te doen op basis van de testgegevens. Ten slotte worden de resultaten gevisualiseerd met een grafiek die de trainingsgegevens, het voorspelde gemiddelde en het 95% betrouwbaarheidsinterval toont.
verschil tussen een leeuw en een tijger
Implementatie van Gauss-proces in Python
Scikit Leer
Python import matplotlib.pyplot as plt import numpy as np from scipy import linalg from sklearn.gaussian_process import kernels,GaussianProcessRegressor ## check version import sys import sklearn print(sys.version) !python --version print("numpy:", np.__version__) print("sklearn:",sklearn.__version__)> De benodigde bibliotheken voor Gaussian Process Regression (GPR) in Python worden door deze code geïmporteerd; dit zijn SciPy voor lineaire algebrafuncties, NumPy voor numerieke bewerkingen, en Matplotlib voor datavisualisatie. Om er zeker van te zijn dat het compatibel is met de benodigde pakketten, verifieert het bovendien de versie van Python en drukt deze af, samen met de versies van NumPy en scikit-learn (sklearn).
Kernelselectie
Python np.random.seed(0) n=50 kernel_ =[kernels.RBF (), kernels.RationalQuadratic(), kernels.ExpSineSquared(periodicity=10.0), kernels.DotProduct(sigma_0=1.0)**2, kernels.Matern() ] print(kernel_, '
')> Uitgang:
[RBF(lengte_schaal=1),
RationeelKwadratisch(alfa=1, lengte_schaal=1),
ExpSineSquared(lengte_schaal=1, periodiciteit=10),
PuntProduct(sigma_0=1) ** 2,
Moederlijk(lengte_schaal=1, nu=1,5)]
De code specificeert het aantal testlocaties (n) en initialiseert a willekeurig zaad . Om de gekozen kernels weer te geven, genereert het een lijst met verschillende kernelfuncties en drukt de lijst af.
Kernelvergelijking en visualisatie
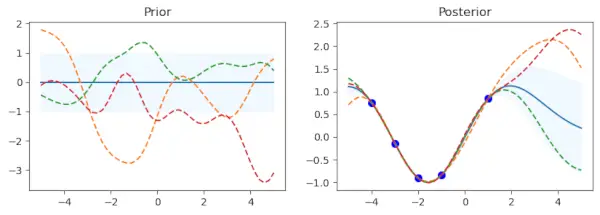
Python for kernel in kernel_: # Gaussian process gp = GaussianProcessRegressor(kernel=kernel) # Prior x_test = np.linspace(-5, 5, n).reshape(-1, 1) mu_prior, sd_prior = gp.predict(x_test, return_std=True) samples_prior = gp.sample_y(x_test, 3) # plot plt.figure(figsize=(10, 3)) plt.subplot(1, 2, 1) plt.plot(x_test, mu_prior) plt.fill_between(x_test.ravel(), mu_prior - sd_prior, mu_prior + sd_prior, color='aliceblue') plt.plot(x_test, samples_prior, '--') plt.title('Prior') # Fit x_train = np.array([-4, -3, -2, -1, 1]).reshape(-1, 1) y_train = np.sin(x_train) gp.fit(x_train, y_train) # posterior mu_post, sd_post = gp.predict(x_test, return_std=True) mu_post = mu_post.reshape(-1) samples_post = np.squeeze(gp.sample_y(x_test, 3)) # plot plt.subplot(1, 2, 2) plt.plot(x_test, mu_post) plt.fill_between(x_test.ravel(), mu_post - sd_post, mu_post + sd_post, color='aliceblue') plt.plot(x_test, samples_post, '--') plt.scatter(x_train, y_train, c='blue', s=50) plt.title('Posterior') plt.show() print("gp.kernel_", gp.kernel_) print("gp.log_marginal_likelihood:", gp.log_marginal_likelihood(gp.kernel_.theta)) print('-'*50, '
')> Uitgang:
RBF
gp.kernel_RBF(lengte_schaal=1,93)
gp.log_marginal_likelihood: -3.444937833462133
--------------------------------------------- -
Rationeel kwadratisch

gp.kernel_ RationalQuadratic(alpha=1e+05, lengte_schaal=1,93)
gp.log_marginal_likelihood: -3.4449718909150966
---------------------------------------------
ExpSinekwadraat

gp.kernel_ ExpSineSquared(length_scale=0,000524, periodiciteit=2,31e+04)
gp.log_marginal_likelihood: -3.4449381454930217
---------------------------------------------
Punt product

gp.kernel_DotProduct(sigma_0=0,998) ** 2
gp.log_marginal_likelihood: -150204291.56018084
---------------------------------------------
Moederlijk

gp.kernel_ Matern(lengte_schaal=1,99, nu=1,5)
gp.log_marginal_likelihood: -5.131637070524745
---------------------------------------------
De code begint met het doorlopen van de verschillende kernelfuncties die in de kernel_list staan vermeld. Er wordt een Gaussiaanse procesregressor (gp) gemaakt met behulp van de specifieke kernel voor elke kernel. Voor het Gaussiaanse proces wordt hiermee de covariantiestructuur vastgesteld. Om de vorige verdeling te beoordelen, wordt een set testinvoerpunten, x_test genaamd, vastgesteld, met waarden variërend van -5 tot 5. Deze set punten wordt omgezet in een kolomvector.
tekenreeks naar json-object converteren
Met behulp van de gp.predict-methode worden op elk testpunt het gemiddelde (mu_prior) en de standaarddeviatie (sd_prior) van de eerdere verdeling bepaald. Standaardafwijkingswaarden worden opgevraagd met de optie return_std=True. gp.sample_y (x_test, 3) wordt gebruikt om drie functievoorbeelden uit de vorige distributie te verkrijgen.
De eerste subplot toont het gemiddelde van de vorige verdeling, waarbij de standaarddeviatie wordt weergegeven door een gearceerd gebied. De monsters worden als stippellijnen over elkaar heen gelegd, terwijl het gemiddelde als een ononderbroken lijn wordt weergegeven. Er is een subplot genaamd Prior. Er is een gedefinieerde set trainingsgegevenspunten (x_train) en doelwaarden (y_train) die daarbij horen. Het Gaussiaanse procesmodel wordt aangepast met behulp van deze punten (gp.fit(x_train, y_train)). Vijf gegevenspunten met bijbehorende sinuswaarden vormen de trainingsgegevens in deze code.
Na de aanpassingsfase van de trainingsgegevens berekent de procedure het gemiddelde van de posterieure verdeling (mu_post) en de standaarddeviatie (sd_post) voor dezelfde testpunten (x_test). gp.sample_y(x_test, 3) wordt ook gebruikt om functiemonsters uit de posterieure distributie te produceren. Het tweede subplot legt de bemonsterde functies als stippellijnen over elkaar heen en toont het gemiddelde van de posterieure verdeling, gearceerd met de standaarddeviatie. In blauw zijn de trainingsgegevenspunten weergegeven. Het subplot heeft de naam Posterior.
Om de vorige en latere plots voor de huidige kernel te zien en een visueel inzicht te krijgen in het gedrag van het model, roept u de functie plt.show() van Matplotlib aan.
De code toont details over de huidige kernel, zoals gp.kernel_, wat aangeeft welke huidige kernel wordt gebruikt, en gp.log_marginale_waarschijnlijkheid (gp.kernel_.theta), wat de log marginale waarschijnlijkheid geeft van het model dat de huidige kernel gebruikt, na elke set eerdere en latere plots.
Voordelen van Gaussiaanse procesregressie (GPR)
Gaussiaanse procesregressie (GPR) heeft een aantal voordelen in een reeks toepassingen:
- GPR biedt een probabilistisch raamwerk voor regressie, wat betekent dat het niet alleen puntschattingen geeft, maar ook onzekerheidsschattingen voor voorspellingen.
- Het is zeer flexibel en kan complexe relaties in de gegevens vastleggen.
- GPR kan worden aangepast aan verschillende toepassingen, waaronder tijdreeksvoorspellingen, optimalisatie en Bayesiaanse optimalisatie.
Uitdagingen van Gaussiaanse procesregressie (GPR)
- GPR kan rekenkundig duur zijn bij het omgaan met grote datasets, omdat de inversie van een covariantiematrix vereist is.
- De keuze van de kernelfunctie en de hyperparameters ervan kunnen een aanzienlijke invloed hebben op de prestaties van het model.
Goede voorbeelden van GPR-toepassingen
- Voorspelling van de aandelenkoers: GPR kan worden gebruikt om aandelenkoersen te modelleren en te voorspellen, rekening houdend met de volatiliteit en onzekerheid op de financiële markten.
- Computerexperimenten: GPR is nuttig bij het optimaliseren van complexe simulaties door de input-output-relaties te modelleren en de meest invloedrijke parameters te identificeren.
- Onregelmatigheidsdetectie: GPR kan worden toegepast op anomaliedetectie, waarbij het ongebruikelijke patronen in tijdreeksgegevens identificeert door normale gegevensverdelingen vast te leggen.
Conclusie
Concluderend is Gaussiaanse procesregressie een waardevol hulpmiddel voor data-analyse en -voorspelling in situaties waarin het begrijpen van de onzekerheid in voorspellingen essentieel is. Door gebruik te maken van probabilistische modellering en kernelfuncties kan GPR nauwkeurige en interpreteerbare resultaten opleveren. Het is echter van cruciaal belang om rekening te houden met de rekenkosten en de behoefte aan deskundige input bij de implementatie van GPR in de praktijk.
