FLOYD WARSHALL-ALGORITME

De Floyd-Warshall-algoritme , genoemd naar de makers ervan Robert Floyd en Stephen Warshall , is een fundamenteel algoritme in de informatica en grafentheorie. Het wordt gebruikt om de kortste paden tussen alle paren knooppunten in een gewogen grafiek te vinden. Dit algoritme is zeer efficiënt en kan met beide grafieken overweg positief en N negatieve randgewichten , waardoor het een veelzijdig hulpmiddel is voor het oplossen van een breed scala aan netwerk- en connectiviteitsproblemen.

Inhoudsopgave

Floyd Warshall-algoritme
Idee achter het Floyd Warshall-algoritme
Floyd Warshall-algoritme Algoritme
Pseudo-code van Floyd Warshall-algoritme
Illustratie van het Floyd Warshall-algoritme
Complexiteitsanalyse van het Floyd Warshall-algoritme
Waarom het Floyd-Warshall-algoritme beter is voor compacte grafieken en niet voor dunne grafieken?
Belangrijke interviewvragen met betrekking tot Floyd-Warshall
Toepassingen in de echte wereld van het Floyd-Warshall-algoritme

Floyd-Warshall-Algoritme-banner

Floyd Warshall-algoritme:

De Floyd Warshall-algoritme is een all-pair kortste pad-algoritme, in tegenstelling tot Dijkstra En Bellman Ford dit zijn kortste pad-algoritmen met één bron. Dit algoritme werkt voor zowel de gericht En ongericht gewogen grafieken. Maar het werkt niet voor grafieken met negatieve cycli (waarbij de som van de randen in een cyclus negatief is). Het volgt Dynamisch programmeren aanpak om elk mogelijk pad dat via elk mogelijk knooppunt gaat te controleren om zo de kortste afstand tussen elk paar knooppunten te berekenen.
hoe u kolommen uit verschillende tabellen in sql selecteert

Idee achter het Floyd Warshall-algoritme:

Stel dat we een grafiek hebben G[][] met IN hoekpunten van 1 naar N . Nu moeten we a beoordelen kortstePadMatrix[][] waar s hortestPathMatrix[i][j] vertegenwoordigt het kortste pad tussen hoekpunten i En J .

Uiteraard de kortste weg ertussen i naar J zal er een paar hebben k aantal tussenliggende knooppunten. Het idee achter het Floyd Warshall-algoritme is om elk hoekpunt te behandelen 1 naar N één voor één als tussenknooppunt.

De volgende afbeelding toont de bovenstaande optimale substructuureigenschap in het Floyd Warshall-algoritme:

Floyd Warshall-algoritme Algoritme:

Initialiseer de oplossingsmatrix op dezelfde manier als de invoergrafiekmatrix als eerste stap.
Werk vervolgens de oplossingsmatrix bij door alle hoekpunten als tussenliggende hoekpunten te beschouwen.
Het idee is om alle hoekpunten één voor één te kiezen en alle kortste paden bij te werken, inclusief het gekozen hoekpunt als tussenliggend hoekpunt in het kortste pad.
Wanneer we het hoekpuntnummer kiezen k als tussenpunt hebben we al rekening gehouden met hoekpunten {0, 1, 2, .. k-1} als tussenliggende hoekpunten.
Voor elk paar (ik, j) van respectievelijk de bron- en bestemmingshoekpunten zijn er twee mogelijke gevallen.
- k is geen tussenliggend hoekpunt op de kortste weg van i naar J . Wij behouden de waarde van dist[i][j] zoals het is.
- k is een tussenliggend hoekpunt op de kortste weg van i naar J . We updaten de waarde van dist[i][j] als dist[i][k] + dist[k][j], als dist[i][j]> dist[i][k] + dist[k][j]

Pseudo-code van Floyd Warshall-algoritme:`>`

Voor k = 0 tot n – 1
Voor i = 0 tot n – 1
Voor j = 0 tot n – 1
Afstand[i, j] = min(Afstand[i, j], Afstand[i, k] + Afstand[k, j])
SQL-volgorde willekeurig

waarbij i = bronknooppunt, j = bestemmingsknooppunt, k = tussenknooppunt

Illustratie van het Floyd Warshall-algoritme:

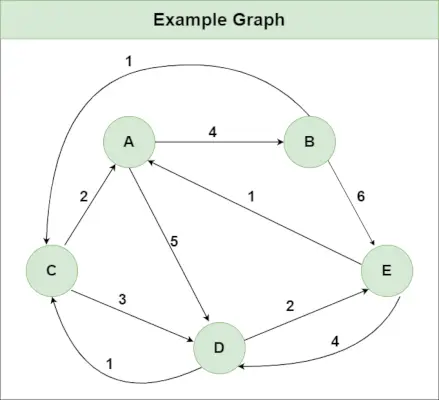
Stel dat we een grafiek hebben zoals weergegeven in de afbeelding:

Stap 1 : Initialiseer de afstand[][]-matrix met behulp van de invoergrafiek, zodat Afstand[i][j]= gewicht van de rand vanaf i naar J , ook Afstand[i][j] = Oneindig als er geen rand van is i naar J.

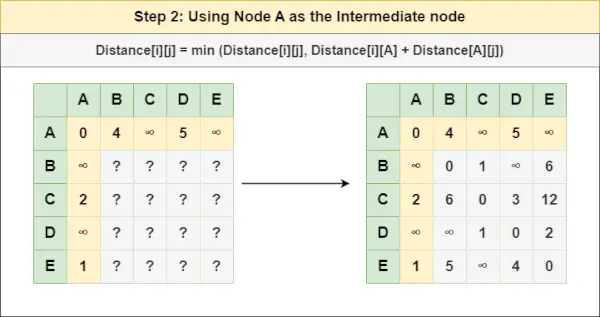
Stap 2 : Behandel knooppunt A als tussenliggend knooppunt en bereken de Afstand[][] voor elk {i,j} knooppuntenpaar met behulp van de formule:

= Afstand[i][j] = minimum (Afstand[i][j], (Afstand van i tot A ) + (Afstand vanaf A naar j))
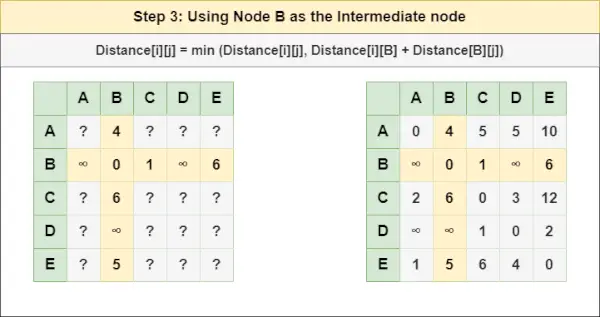
= Afstand[i][j] = minimum (Afstand[i][j], Afstand[i][ A ] + Afstand[ A ][J])

Stap 3 : Behandel knooppunt B als tussenliggend knooppunt en bereken de Afstand[][] voor elk {i,j} knooppuntenpaar met behulp van de formule:

= Afstand[i][j] = minimum (Afstand[i][j], (Afstand van i tot B ) + (Afstand vanaf B naar j))
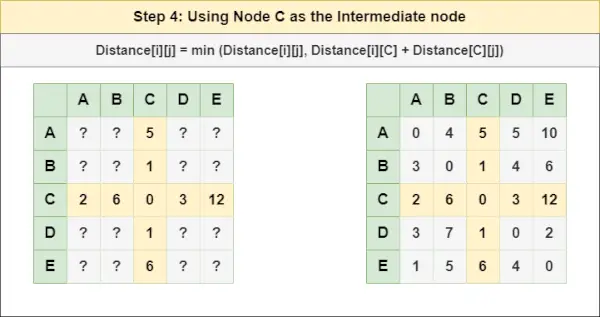
= Afstand[i][j] = minimum (Afstand[i][j], Afstand[i][ B ] + Afstand[ B ][J])

Stap 4 : Behandel knooppunt C als tussenliggend knooppunt en bereken de Afstand[][] voor elk {i,j} knooppuntenpaar met behulp van de formule:

= Afstand[i][j] = minimum (Afstand[i][j], (Afstand van i tot C ) + (Afstand vanaf C naar j))
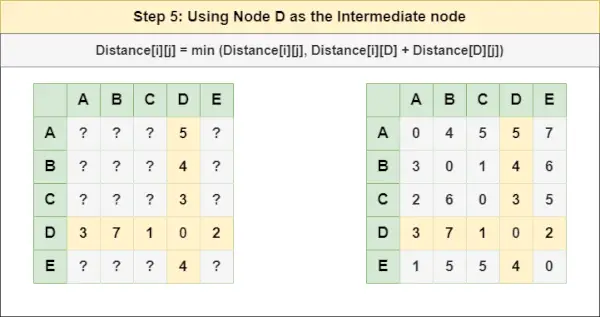
= Afstand[i][j] = minimum (Afstand[i][j], Afstand[i][ C ] + Afstand[ C ][J])

Stap 5 : Behandel knooppunt D als tussenliggend knooppunt en bereken de Afstand[][] voor elk {i,j} knooppuntenpaar met behulp van de formule:
Hoe de applicatie zichtbaar te maken in Android

= Afstand[i][j] = minimum (Afstand[i][j], (Afstand van i tot D ) + (Afstand vanaf D naar j))
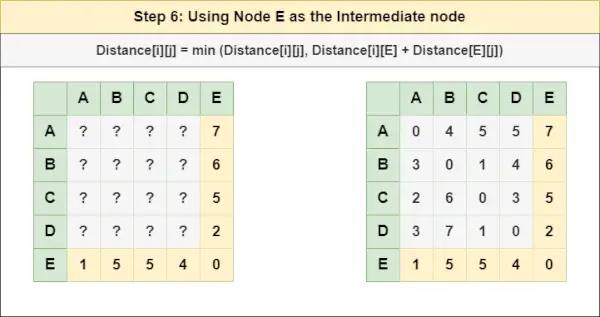
= Afstand[i][j] = minimum (Afstand[i][j], Afstand[i][ D ] + Afstand[ D ][J])

Stap 6 : Behandel knooppunt EN als tussenliggend knooppunt en bereken de Afstand[][] voor elk {i,j} knooppuntenpaar met behulp van de formule:

= Afstand[i][j] = minimum (Afstand[i][j], (Afstand van i tot EN ) + (Afstand vanaf EN naar j))
= Afstand[i][j] = minimum (Afstand[i][j], Afstand[i][ EN ] + Afstand[ EN ][J])

Stap 7 : Omdat alle knooppunten zijn behandeld als een tussenliggend knooppunt, kunnen we nu de bijgewerkte afstand[][]-matrix retourneren als onze antwoordmatrix.
Java-bubbel sorteren

Aanbevolen praktijk Probeer het!

Hieronder vindt u de implementatie van de bovenstaande aanpak:

C++

 // C++ Program for Floyd Warshall Algorithm #include  using namespace std; // Number of vertices in the graph #define V 4 /* Define Infinite as a large enough value.This value will be used for vertices not connected to each other */ #define INF 99999 // A function to print the solution matrix void printSolution(int dist[][V]); // Solves the all-pairs shortest path // problem using Floyd Warshall algorithm void floydWarshall(int dist[][V]) {  int i, j, k;  /* Add all vertices one by one to  the set of intermediate vertices.  --->Voordat een iteratie begint, hebben we de kortste afstanden tussen alle paren hoekpunten, zodat de kortste afstanden alleen de hoekpunten in verzameling {0, 1, 2, .. k-1} als tussenliggende hoekpunten beschouwen.  ----> Na het einde van een iteratie, hoekpunt nr. k wordt toegevoegd aan de set tussenliggende hoekpunten en de set wordt {0, 1, 2, .. k} */ for (k = 0; k< V; k++) {  // Pick all vertices as source one by one  for (i = 0; i < V; i++) {  // Pick all vertices as destination for the  // above picked source  for (j = 0; j < V; j++) {  // If vertex k is on the shortest path from  // i to j, then update the value of  // dist[i][j]  if (dist[i][j]>(dist[i][k] + dist[k][j]) && (dist[k][j] != INF && dist[i][k] != INF)) dist[i][j] = dist[i][k] + dist[k][j];  } } } // Druk de kortste afstand af matrix printSolution(dist); } /* Een hulpprogramma voor het afdrukken van oplossingen */ void printSolution(int dist[][V]) { cout<< 'The following matrix shows the shortest '  'distances'  ' between every pair of vertices 
';  for (int i = 0; i < V; i++) {  for (int j = 0; j < V; j++) {  if (dist[i][j] == INF)  cout << 'INF'  << ' ';  else  cout << dist[i][j] << ' ';  }  cout << endl;  } } // Driver's code int main() {  /* Let us create the following weighted graph  10  (0)------->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 */ int grafiek[V][V] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1}, {INF, INF, INF, 0 } };  // Functieaanroep floydWarshall(grafiek);  retour 0; } // Deze code is bijgedragen door Mythri J L>

 // C Program for Floyd Warshall Algorithm #include  // Number of vertices in the graph #define V 4 /* Define Infinite as a large enough  value. This value will be used  for vertices not connected to each other */ #define INF 99999 // A function to print the solution matrix void printSolution(int dist[][V]); // Solves the all-pairs shortest path // problem using Floyd Warshall algorithm void floydWarshall(int dist[][V]) {  int i, j, k;  /* Add all vertices one by one to  the set of intermediate vertices.  --->Voordat een iteratie begint, hebben we de kortste afstanden tussen alle paren hoekpunten, zodat de kortste afstanden alleen de hoekpunten in verzameling {0, 1, 2, .. k-1} als tussenliggende hoekpunten beschouwen.  ----> Na het einde van een iteratie, hoekpunt nr. k wordt toegevoegd aan de set tussenliggende hoekpunten en de set wordt {0, 1, 2, .. k} */ for (k = 0; k< V; k++) {  // Pick all vertices as source one by one  for (i = 0; i < V; i++) {  // Pick all vertices as destination for the  // above picked source  for (j = 0; j < V; j++) {  // If vertex k is on the shortest path from  // i to j, then update the value of  // dist[i][j]  if (dist[i][k] + dist[k][j] < dist[i][j])  dist[i][j] = dist[i][k] + dist[k][j];  }  }  }  // Print the shortest distance matrix  printSolution(dist); } /* A utility function to print solution */ void printSolution(int dist[][V]) {  printf(  'The following matrix shows the shortest distances'  ' between every pair of vertices 
');  for (int i = 0; i < V; i++) {  for (int j = 0; j < V; j++) {  if (dist[i][j] == INF)  printf('%7s', 'INF');  else  printf('%7d', dist[i][j]);  }  printf('
');  } } // driver's code int main() {  /* Let us create the following weighted graph  10  (0)------->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 */ int grafiek[V][V] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1}, {INF, INF, INF, 0 } };  // Functieaanroep floydWarshall(grafiek);  retour 0; }>

Java

 // Java program for Floyd Warshall All Pairs Shortest // Path algorithm. import java.io.*; import java.lang.*; import java.util.*; class AllPairShortestPath {  final static int INF = 99999, V = 4;  void floydWarshall(int dist[][])  {  int i, j, k;  /* Add all vertices one by one  to the set of intermediate  vertices.  --->Voordat een iteratie begint, hebben we de kortste afstanden tussen alle paren hoekpunten, zodat de kortste afstanden alleen de hoekpunten in verzameling {0, 1, 2, .. k-1} als tussenliggende hoekpunten beschouwen.  ----> Na het einde van een iteratie, hoekpunt nr. k wordt toegevoegd aan de set tussenliggende hoekpunten en de set wordt {0, 1, 2, .. k} */ for (k = 0; k< V; k++) {  // Pick all vertices as source one by one  for (i = 0; i < V; i++) {  // Pick all vertices as destination for the  // above picked source  for (j = 0; j < V; j++) {  // If vertex k is on the shortest path  // from i to j, then update the value of  // dist[i][j]  if (dist[i][k] + dist[k][j]  < dist[i][j])  dist[i][j]  = dist[i][k] + dist[k][j];  }  }  }  // Print the shortest distance matrix  printSolution(dist);  }  void printSolution(int dist[][])  {  System.out.println(  'The following matrix shows the shortest '  + 'distances between every pair of vertices');  for (int i = 0; i < V; ++i) {  for (int j = 0; j < V; ++j) {  if (dist[i][j] == INF)  System.out.print('INF ');  else  System.out.print(dist[i][j] + ' ');  }  System.out.println();  }  }  // Driver's code  public static void main(String[] args)  {  /* Let us create the following weighted graph  10  (0)------->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 */ int grafiek[][] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1 }, {INF, INF, INF, 0 } };  AllPairShortestPath a = nieuw AllPairShortestPath();  // Functieaanroep a.floydWarshall(grafiek);  } } // Bijgedragen door Aakash Hasija>

Python3

 # Python3 Program for Floyd Warshall Algorithm # Number of vertices in the graph V = 4 # Define infinity as the large # enough value. This value will be # used for vertices not connected to each other INF = 99999 # Solves all pair shortest path # via Floyd Warshall Algorithm def floydWarshall(graph):  ''' dist[][] will be the output   matrix that will finally  have the shortest distances   between every pair of vertices '''  ''' initializing the solution matrix   same as input graph matrix  OR we can say that the initial   values of shortest distances  are based on shortest paths considering no   intermediate vertices ''' dist = list(map(lambda i: list(map(lambda j: j, i)), graph))  ''' Add all vertices one by one   to the set of intermediate  vertices.  --->Voordat een iteratie begint, hebben we de kortste afstanden tussen alle paren hoekpunten, zodat de kortste afstanden alleen de hoekpunten in de verzameling {0, 1, 2, .. k-1} als tussenliggende hoekpunten beschouwen.  ----> Na het einde van een iteratie, hoekpunt nr. k wordt toegevoegd aan de set tussenliggende hoekpunten en de set wordt {0, 1, 2, .. k} ''' voor k in bereik(V): # kies alle hoekpunten één voor één als bron voor i in range(V): # Kies alle hoekpunten als bestemming voor de # hierboven gekozen bron voor j in range(V): # Als hoekpunt k zich op het kortste pad van # i naar j bevindt, update dan de waarde van dist[i][ j] dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j] ) printSolution(dist) # Een hulpprogrammafunctie om de oplossing def printSolution af te drukken (dist): print('De volgende matrix toont de kortste afstanden tussen elk paar hoekpunten') voor i binnen bereik(V): voor j binnen bereik(V): if(dist[i][j] == INF): print('%7s' % ('INF'), end=' ') else: print('%7d	' % (dist[i][j]), end=' ') if j == V-1: print() # Stuurprogrammacode if __name__ == '__main__': ''' 10 (0)------ ->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 ''' grafiek = [[0, 5, INF, 10], [INF, 0, 3, INF], [INF, INF, 0 , 1], [INF, INF, INF, 0] ] # Functieaanroep floydWarshall(graph) # Deze code is bijgedragen door Mythri J L>

 // C# program for Floyd Warshall All // Pairs Shortest Path algorithm. using System; public class AllPairShortestPath {  readonly static int INF = 99999, V = 4;  void floydWarshall(int[, ] graph)  {  int[, ] dist = new int[V, V];  int i, j, k;  // Initialize the solution matrix  // same as input graph matrix  // Or we can say the initial  // values of shortest distances  // are based on shortest paths  // considering no intermediate  // vertex  for (i = 0; i < V; i++) {  for (j = 0; j < V; j++) {  dist[i, j] = graph[i, j];  }  }  /* Add all vertices one by one to  the set of intermediate vertices.  --->Voordat een iteratie begint, hebben we de kortste afstanden tussen alle paren hoekpunten, zodat de kortste afstanden alleen de hoekpunten in verzameling {0, 1, 2, .. k-1} als tussenliggende hoekpunten beschouwen.  ---> Na het einde van een iteratie, hoekpunt nr. k wordt toegevoegd aan de set tussenliggende hoekpunten en de set wordt {0, 1, 2, .. k} */ for (k = 0; k< V; k++) {  // Pick all vertices as source  // one by one  for (i = 0; i < V; i++) {  // Pick all vertices as destination  // for the above picked source  for (j = 0; j < V; j++) {  // If vertex k is on the shortest  // path from i to j, then update  // the value of dist[i][j]  if (dist[i, k] + dist[k, j]  < dist[i, j]) {  dist[i, j]  = dist[i, k] + dist[k, j];  }  }  }  }  // Print the shortest distance matrix  printSolution(dist);  }  void printSolution(int[, ] dist)  {  Console.WriteLine(  'Following matrix shows the shortest '  + 'distances between every pair of vertices');  for (int i = 0; i < V; ++i) {  for (int j = 0; j < V; ++j) {  if (dist[i, j] == INF) {  Console.Write('INF ');  }  else {  Console.Write(dist[i, j] + ' ');  }  }  Console.WriteLine();  }  }  // Driver's Code  public static void Main(string[] args)  {  /* Let us create the following  weighted graph  10  (0)------->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 */ int[, ] grafiek = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0 , 1 }, {INF, INF, INF, 0 } };  AllPairShortestPath a = nieuw AllPairShortestPath();  // Functieaanroep a.floydWarshall(grafiek);  } } // Dit artikel is bijgedragen door // Abdul Mateen Mohammed>

Javascript

 // A JavaScript program for Floyd Warshall All  // Pairs Shortest Path algorithm.  var INF = 99999;  class AllPairShortestPath {  constructor() {  this.V = 4;  }  floydWarshall(graph) {  var dist = Array.from(Array(this.V), () =>nieuwe Array(this.V).fill(0));  var ik, j, k;  // Initialiseer de oplossingsmatrix // hetzelfde als de invoergrafiekmatrix // Of we kunnen zeggen dat de initiële // waarden van de kortste afstanden // zijn gebaseerd op de kortste paden // zonder tussenliggend // hoekpunt voor (i = 0; i< this.V; i++) {  for (j = 0; j < this.V; j++) {  dist[i][j] = graph[i][j];  }  }  /* Add all vertices one by one to  the set of intermediate vertices.  --->Voordat een iteratie begint, hebben we de kortste afstanden tussen alle paren hoekpunten, zodat de kortste afstanden alleen de hoekpunten in verzameling {0, 1, 2, .. k-1} als tussenliggende hoekpunten beschouwen.  ---> Na het einde van een iteratie, hoekpunt nr. k wordt toegevoegd aan de set tussenliggende hoekpunten en de set wordt {0, 1, 2, .. k} */ for (k = 0; k< this.V; k++) {  // Pick all vertices as source  // one by one  for (i = 0; i < this.V; i++) {  // Pick all vertices as destination  // for the above picked source  for (j = 0; j < this.V; j++) {  // If vertex k is on the shortest  // path from i to j, then update  // the value of dist[i][j]  if (dist[i][k] + dist[k][j] < dist[i][j]) {  dist[i][j] = dist[i][k] + dist[k][j];  }  }  }  }  // Print the shortest distance matrix  this.printSolution(dist);  }  printSolution(dist) {  document.write(  'Following matrix shows the shortest ' +  'distances between every pair of vertices '  );  for (var i = 0; i < this.V; ++i) {  for (var j = 0; j < this.V; ++j) {  if (dist[i][j] == INF) {  document.write(' INF ');  } else {  document.write('  ' + dist[i][j] + ' ');  }  }  document.write(' ');  }  }  }  // Driver Code  /* Let us create the following  weighted graph  10  (0)------->(3) | /| 5 | |  | | 1 |/ |  (1)------->(2) 3 */ var grafiek = [ [0, 5, INF, 10], [INF, 0, 3, INF], [INF, INF, 0, 1] , [INF, INF, INF, 0], ];  var a = nieuw AllPairShortestPath();  // Druk de oplossing af a.floydWarshall(graph);    // Deze code is bijgedragen door rdtaank.>

PHP

  // PHP Program for Floyd Warshall Algorithm  // Solves the all-pairs shortest path problem // using Floyd Warshall algorithm  function floydWarshall ($graph, $V, $INF) { /* dist[][] will be the output matrix   that will finally have the shortest   distances between every pair of vertices */ $dist = array(array(0,0,0,0), array(0,0,0,0), array(0,0,0,0), array(0,0,0,0)); /* Initialize the solution matrix same   as input graph matrix. Or we can say the   initial values of shortest distances are   based on shortest paths considering no   intermediate vertex. */ for ($i = 0; $i < $V; $i++) for ($j = 0; $j < $V; $j++) $dist[$i][$j] = $graph[$i][$j]; /* Add all vertices one by one to the set   of intermediate vertices.   --->Voordat een iteratie begint, hebben we de kortste afstanden tussen alle paren hoekpunten, zodat de kortste afstanden alleen de hoekpunten in verzameling {0, 1, 2, .. k-1} als tussenliggende hoekpunten beschouwen.   ----> Na het einde van een iteratie, hoekpunt nr. k wordt toegevoegd aan de set tussenliggende hoekpunten en de set wordt {0, 1, 2, .. k} */ for ($k = 0; $k< $V; $k++) { // Pick all vertices as source one by one  for ($i = 0; $i < $V; $i++) { // Pick all vertices as destination  // for the above picked source  for ($j = 0; $j < $V; $j++) { // If vertex k is on the shortest path from  // i to j, then update the value of dist[i][j]  if ($dist[$i][$k] + $dist[$k][$j] < $dist[$i][$j]) $dist[$i][$j] = $dist[$i][$k] + $dist[$k][$j]; } } } // Print the shortest distance matrix  printSolution($dist, $V, $INF); } /* A utility function to print solution */ function printSolution($dist, $V, $INF) { echo 'The following matrix shows the ' . 'shortest distances between ' . 'every pair of vertices 
'; for ($i = 0; $i < $V; $i++) { for ($j = 0; $j < $V; $j++) { if ($dist[$i][$j] == $INF) echo 'INF ' ; else echo $dist[$i][$j], ' '; } echo '
'; } } // Drivers' Code // Number of vertices in the graph  $V = 4 ; /* Define Infinite as a large enough  value. This value will be used for vertices not connected to each other */ $INF = 99999 ; /* Let us create the following weighted graph   10  (0)------->(3) | /| 5 | |   | | 1 |/ |  (1)------->(2) 3 */ $graph = array(array(0, 5, $INF, 10), array($INF, 0, 3, $INF), array($ INF, $INF, 0, 1), array($INF, $INF, $INF, 0)); // Functieaanroep floydWarshall($graph, $V, $INF); // Deze code is bijgedragen door Ryuga ?>>

Uitvoer

The following matrix shows the shortest distances between every pair of vertices 0 5 8 9 INF 0 3 4 INF INF 0 1 INF INF INF 0>

Complexiteitsanalyse van het Floyd Warshall-algoritme:

Tijdcomplexiteit: O(V³), waarbij V het aantal hoekpunten in de grafiek is en we drie geneste lussen van elk maat V uitvoeren
Hulpruimte: O(V²), om een 2D-matrix te creëren om de kortste afstand voor elk paar knooppunten op te slaan.

Opmerking : Bovenstaand programma drukt alleen de kortste afstanden af. We kunnen de oplossing aanpassen om de kortste paden af te drukken, ook door de voorgangerinformatie in een aparte 2D-matrix op te slaan.

Waarom het Floyd-Warshall-algoritme beter is voor compacte grafieken en niet voor dunne grafieken?

Dichte grafiek : Een grafiek waarin het aantal randen aanzienlijk veel hoger is dan het aantal hoekpunten.
Schaarse grafiek : Een grafiek waarin het aantal randen erg laag is.

Het maakt niet uit hoeveel randen er in de grafiek zijn Floyd Warshall-algoritme loopt voor O(V³) tijden waarvoor het het meest geschikt is Dichte grafieken . In het geval van schaarse grafieken, Johnson’s algoritme is geschikter.

Hoe kan ik een negatieve cyclus in een grafiek detecteren met behulp van het Floyd Warshall-algoritme?
Hoe verschilt het Floyd-Warshall-algoritme van het algoritme van Dijkstra?
Hoe verschilt het Floyd-Warshall-algoritme van het Bellman-Ford-algoritme?

Toepassingen in de echte wereld van het Floyd-Warshall-algoritme:

Bij computernetwerken kan het algoritme worden gebruikt om het kortste pad tussen alle paren knooppunten in een netwerk te vinden. Dit wordt genoemd als netwerk routering .
Vluchtconnectiviteit In de luchtvaartindustrie wordt het kortste pad tussen de luchthavens gevonden.
GIS ( Geografische Informatie Systemen ) toepassingen omvatten vaak het analyseren van ruimtelijke gegevens, zoals wegennetwerken, om de kortste paden tussen locaties te vinden.
Het algoritme van Kleene wat een generalisatie is van Floyd Warshall, kan worden gebruikt om reguliere expressies voor een reguliere taal te vinden.