• Finite state machine wordt gebruikt om patronen te herkennen.
• Eindige automatenmachine neemt de tekenreeks als invoer en verandert de status dienovereenkomstig. Wanneer in de invoer een gewenst symbool wordt gevonden, vindt de overgang plaats.
• Tijdens de overgang kunnen de automaten naar de volgende staat gaan of in dezelfde staat blijven.
• FA heeft twee staten: status accepteren of status afwijzen. Wanneer de invoerreeks met succes is verwerkt en de automaat zijn eindstatus heeft bereikt, zal deze accepteren.

Een eindige automaat bestaat uit het volgende:

Vraag: eindige reeks toestanden
∑: eindige set invoersymbolen
q0: begintoestand
F: eindtoestand
d: Overgangsfunctie

Overgangsfunctie kan worden gedefinieerd als

 δ: Q x ∑ →Q 

FA wordt op twee manieren gekarakteriseerd:

1. DFA (eindige automaten)
2. NDFA (niet-deterministische eindige automaten)

DFA

DFA staat voor Deterministische Eindige Automaten. Deterministisch verwijst naar het unieke karakter van de berekening. In DFA gaat het invoerteken slechts naar één status. DFA accepteert de nulbeweging niet, wat betekent dat de DFA de status niet kan wijzigen zonder enig invoerteken.

DFA heeft vijf tupels {Q, ∑, q0, F, δ}

Voorbeeld

Zie een voorbeeld van deterministische eindige automaten:

 Q = {q0, q1, q2} ∑ = {0, 1} q0 = {q0} F = {q3}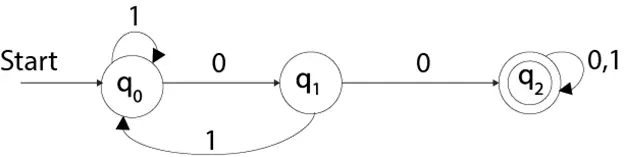 

NDFA

NDFA verwijst naar de niet-deterministische eindige automaten. Het wordt gebruikt om een ​​willekeurig aantal toestanden voor een bepaalde invoer te doorlopen. NDFA accepteert de NULL-beweging, wat betekent dat de status kan worden gewijzigd zonder de symbolen te lezen.

NDFA heeft ook vijf staten, net als DFA. Maar NDFA heeft een andere overgangsfunctie.

Overgangsfunctie van NDFA kan worden gedefinieerd als:

Voorbeeld

Zie een voorbeeld van niet-deterministische eindige automaten:

 Q = {q0, q1, q2} ∑ = {0, 1} q0 = {q0} F = {q3}