Voorbeeld 1:
Ontwerp een NFA voor de transitietabel, zoals hieronder weergegeven:
| Huidige staat | 0 | 1 |
|---|---|---|
| →q0 | q0, q1 | q0, q2 |
| q1 | Q3 | e |
| Q2 | q2, q3 | Q3 |
| →q3 | Q3 | Q3 |
Oplossing:
Java-variabele variabele
Het overgangsdiagram kan worden getekend met behulp van de mappingfunctie zoals weergegeven in de tabel.
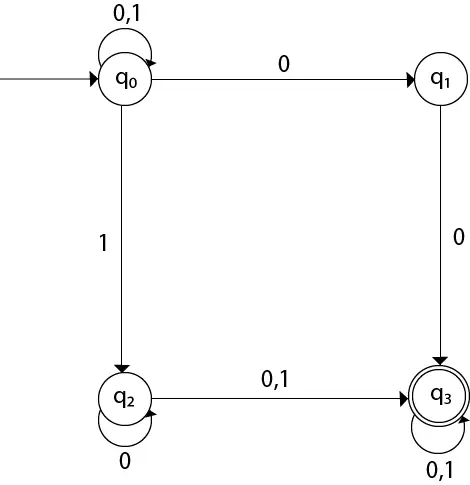
Hier,
δ(q0, 0) = {q0, q1} δ(q0, 1) = {q0, q2} Then, δ(q1, 0) = {q3} Then, δ(q2, 0) = {q2, q3} δ(q2, 1) = {q3} Then, δ(q3, 0) = {q3} δ(q3, 1) = {q3} Voorbeeld 2:
Ontwerp een NFA met ∑ = {0, 1} accepteert alle tekenreeksen die eindigen op 01.
Oplossing:

NFA zou dus zijn:

Voorbeeld 3:
Ontwerp een NFA met ∑ = {0, 1} waarin dubbel '1' wordt gevolgd door dubbel '0'.
Oplossing:
De FA met dubbel 1 is als volgt:

Het moet onmiddellijk worden gevolgd door dubbel 0.
genezing tool gimp
Dan,

Vóór dubbel 1 kan er elke reeks van 0 en 1 zijn. Op dezelfde manier kan er na dubbel 0 elke reeks van 0 en 1 zijn.
Daarom wordt de NFA:

Kijk nu naar de string 01100011
q0 → q1 → q2 → q3 → q4 → q4 → q4 → q4
Voorbeeld 4:
Ontwerp een NFA waarin alle strings een substring 1110 bevatten.
Oplossing:
De taal bestaat uit de gehele tekenreeks die subtekenreeks 1010 bevat. Het gedeeltelijke overgangsdiagram kan er als volgt uitzien:
polymorfisme Java

Nu zou 1010 de subtekenreeks kunnen zijn. Daarom zullen we de ingangen 0's en 1's optellen, zodat de substring 1010 van de taal behouden kan blijven. Daarom wordt de NFA:
Java-constante

Overgangstabel voor het bovenstaande overgangsdiagram vindt u hieronder:
| Huidige staat | 0 | 1 |
|---|---|---|
| →q1 | q1 | q1, q2 |
| Q2 | Q3 | |
| Q3 | Q4 | |
| Q4 | Q5 | *q5 | Q5 | Q5 |
Beschouw een string 111010,
δ(q1, 111010) = δ(q1, 1100) = δ(q1, 100) = δ(q2, 00)
Zat vast! Omdat er geen pad vanuit q2 is voor invoersymbool 0, kunnen we string 111010 op een andere manier verwerken.
δ(q1, 111010) = δ(q2, 1100) = δ(q3, 100) = δ(q4, 00) = δ(q5, 0) = δ(q5, ε)
Omdat toestand q5 de acceptatietoestand is. We krijgen de volledige scan en we hebben de eindtoestand bereikt.
Voorbeeld 5:
Ontwerp een NFA met ∑ = {0, 1} accepteert alle strings waarin het derde symbool vanaf de rechterkant altijd 0 is.
Oplossing:

We krijgen dus het derde symbool van rechts altijd als '0'. De NFA kan zijn:

De bovenstaande afbeelding is een NFA omdat we in toestand q0 met invoer 0 naar toestand q0 of q1 kunnen gaan.
