Trigonometrie is een belangrijke tak van de wiskunde die zich bezighoudt met de relatie tussen de lengtes van zijden en hoeken van een rechthoekige driehoek. Sinus, cosinus, tangens, cosecans, secans en cotangens zijn de zes trigonometrische verhoudingen of functies. Waar een trigonometrische verhouding wordt weergegeven als de verhouding tussen de zijden van een rechthoekige driehoek.

• sin θ = tegenoverliggende zijde/hypotenusa
• cos θ = aangrenzende zijde/hypotenusa
• tan θ = tegenoverliggende zijde/aangrenzende zijde
• cosec θ = 1/sin θ = hypotenusa/overzijde
• sec θ = 1/cos θ = hypotenusa/aangrenzende zijde
• kinderbed θ = 1/tan θ = aangrenzende zijde/tegenoverliggende zijde

Cotangens formule

Een cotangensfunctie is een reciproque functie van de gegeven tangensfunctie. De waarde van een cotangenshoek in een rechthoekige driehoek is de verhouding van de lengte van de zijde grenzend aan de gegeven hoek tot de lengte van de zijde tegenovergesteld aan de gegeven hoek. We schrijven de cotangensfunctie als cot.

Driehoek ABC

De cotangensformule voor de hoek θ is nu:

kinderbedje θ = (Aangrenzende zijde)/(Tegenovergestelde zijde)

• De cotangensfunctie is positief in het eerste en derde kwadrant en negatief in het tweede en vierde kwadrant.

1. kinderbedje (2π + θ) = kinderbedje θ (1^stkwadrant)
2. kinderbedje (π – θ) = – kinderbedje θ (2^nlkwadrant)
3. kinderbedje (π + θ) = kinderbedje θ (3^rdkwadrant)
4. kinderbedje (2π – θ) = – kinderbedje θ (4^ekwadrant)

• De cotangensfunctie is een negatieve functie omdat de cotangens van een negatieve hoek het negatief is van een cotangens positieve hoek.

kinderbedje (-θ) = – kinderbedje θ

• In termen van de tangensfunctie wordt de cotangensfunctie geschreven als:

kinderbed θ = 1/bruin θ

(of)

kinderbed θ = bruin (90° – θ) (of) bruin (π/2 – θ)

• De cotangensfunctie in termen van sinus- en cosinusfuncties kan worden geschreven als:

kinderbed θ = cos θ/sin θ

Dat weten we, kinderbed θ = aangrenzende zijde/tegenoverliggende zijde

Deel nu zowel de teller als de noemer door de hypotenusa

⇒ kinderbed θ = (aangrenzende zijde/hypotenusa) / (tegenoverliggende zijde/hypotenusa)

Dat weten we, sin θ = tegenoverliggende zijde/hypotenusa

cos θ = aangrenzende zijde/hypotenusa

Daarom is cot θ = cos θ/sin θ

• Cotangensfunctie in termen van sinusfunctie kan worden geschreven als,

kinderbed θ = (√1 – zonde ² ik)/zonde ik

Dat weten we: cot θ = cos θ/sin θ

Van de identiteiten van Pythagoras die we hebben;

want²θ + zonde²θ = 1

⇒ cos θ = √1 – zonde²i

Daarom kinderbedje θ =

• Cotangensfunctie in termen van cosinusfunctie kan worden geschreven als,

kinderbed θ = cos θ/(√1 -cos ² i)

Dat weten we: cot θ = cos θ/sin θ

Van de identiteiten van Pythagoras die we hebben;

want²θ + zonde²θ = 1

zonde θ = √1 – cos²i

Daarom kinderbedje θ =

• Cotangensfunctie in termen van secans- en cosecansfuncties kan worden geschreven als,

kinderbed θ = cosec θ/sec θ

We hebben: kinderbed θ = cos θ/sin θ

Dit kan worden geschreven als: kinderbed θ = (1/sin θ) / (1/cos θ)

⇒ kinderbed θ = cosec θ/sec θ

• Cotangensfunctie in termen van cosecante functie kan worden geschreven als:

kinderbedje θ = √(cosec ² - 1)

Van de identiteiten van Pythagoras hebben we:

cosec²θ – kinderbed²θ = 1

⇒ kinderbed²θ = 1 – cosec²- 1

Daarom is bed θ = √(cosec²- 1)

• Cotangensfunctie in termen van secansfunctie kan worden geschreven als:

kinderbedje θ = 1/(√sec ² ik – 1)

Van de identiteiten van Pythagoras hebben we:

sec²θ – dus²θ = 1

bruin θ = √sec²ik – 1

Dat weten we, kinderbed θ = 1/tan θ

Vandaar, kinderbedje θ =

Trigonometrische verhoudingstabel

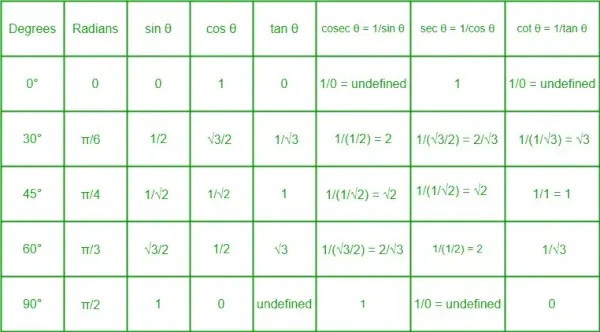
Trigonometrische verhoudingstabel

Cotangentenwet of wet van cotangenten

De cotangenswet lijkt op de sinuswet, maar hier gaat het om halve hoeken. De wet van de cotangens beschrijft de relatie tussen de lengtes van de zijden van de driehoek en de cotangensen van de helften van de drie hoeken. Beschouw een driehoek ABC, waarbij a, b en c de lengtes zijn van de zijden van de driehoek.

De wet van de cotangenten stelt dat:

Waarbij s de halve omtrek is van de driehoek ABC en r de binnenstraal van de ingeschreven cirkel van de driehoek.

s = (een + b + c)/2

r=

Voorbeeldproblemen

Probleem 1: Vind de waarde van kinderbed θ als tan θ = 3/4.

Oplossing:

Gegeven gegevens: tan θ = 3/4

We weten dat, kinderbed θ = 1/bruin θ

⇒ kinderbed θ = 1/(3/4) = 4/3

Dus kinderbedje θ = 4/3

Probleem 2: Vind de waarde van cot α, sin α = 1/3, en cos α = 2√2/3.

Oplossing:

Gegeven gegevens: sin α = 1/3 en cos α = 2√2/3

We weten dat, kinderbed α = cos α/sin α

willekeurig geen generator in Java

⇒ kinderbed α = (2√2/3) / (1/3) = 2√2

Daarom is de waarde van kinderbed α = 2√2

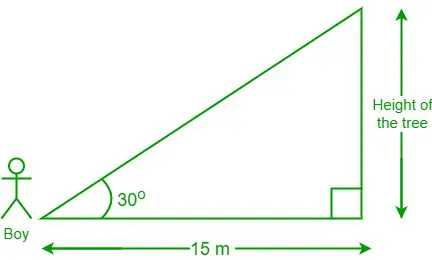
Probleem 3: Een jongen die op 15 meter van een boom staat, kijkt in een hoek van 30 graden naar de top van de boom. Wat is de hoogte van de boom?

Oplossing:

Diagram uit de gegeven gegevens

Gegeven gegevens: de afstand tussen de jongen en de voet van de boom = 15 m en θ = 30°

Laat de hoogte van de boom ‘h’ zijn

We hebben, kinderbedje θ = aangrenzende zijde/tegenoverliggende zijde

⇒ kinderbed 30° = 15/u

⇒ √3 = 15/u [sinds kinderbed 30° = √3]

⇒ h = 15/√3

⇒ h = 5√3 m

De hoogte van de boom is dus 5√3 m

Probleem 4: Vind de waarde van bed x als sec x = 6/5.

Oplossing:

Gegeven gegevens, sec x = 6/5

We hebben, sec ² x-zo ² x = 1

⇒ (6/5)²- Dus²x = 1

⇒ 36/25 – zo²x = 1

⇒ dus²x = 36/25 – 1

⇒ dus²x = 11/25

⇒ bruin x = √(11/25) = √11/5

We weten dat, kinderbed x = 1/bruin x

⇒ kinderbed x = 1/(√11/5) = 5/√11

Daarom kinderbed x = 5/√11

Probleem 5: Vind de waarde van kinderbed θ als cosec θ = 25/24.

Oplossing:

Gegeven gegevens: cosec θ = 25/24

We weten dat, kinderbedje θ = √(cosec ² - 1)

⇒ kinderbed θ = √(25/24)²- 1

⇒ kinderbed θ =√(625 – 576)/576 = √49/576

⇒ kinderbed θ = 7/24

Daarom is de waarde van kinderbed θ = 7/24

Probleem 6: Vind de waarde van kinderbed β als sin β = 5/13.

Oplossing:

Gegeven gegevens: sin β = 5/13

We weten dat, zonder ² β + cos ² β = 1

⇒ (13/5)²+ co²β = 1

⇒ cos²β = 1 – (5/13)²= 1 – 25/169 = 144/169

⇒ cos β = √144/169 = 12/13

wieg β = cosβ/sin β

= (12/13) / (5/13)

⇒ kinderbed β = 12/5

Daarom is de waarde van kinderbed β = 12/5

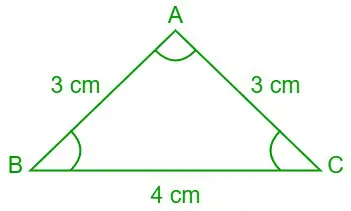
Probleem 7: Vind met behulp van de wet van de cotangensen de waarden van ∠A, ∠B en ∠C (in graden) als de lengtes van de drie zijden van driehoek ABC a = 4 cm, b= 3 cm en c= zijn 3 cm.

Oplossing:

Gegeven: a = 4 cm, b = 3 cm en c = 3 cm

Driehoek ABC

Uit de cotangentenwet volgt

s = (een + b + c)/2

⇒ s = (3 + 4 + 3)/2 = 10/2 = 5

Nu, s – a = 5 – 4 = 1

⇒ s – b = 5 – 3 = 2

⇒ s – c = 5 – 3 = 2

r=

⇒ r = √[(1)(2)(2)/5]

Inradius van de driehoek r = 2/√5

numpy lijnruimte

Uit de vergelijking van de wet van cotangensen,

kinderbedje (A/2)/1 = 1/(2/√5)

⇒ kinderbed (A/2) = √5/2 ⇒ A/2 = kinderbed^-1(√5/2)

⇒ (A/2) = 41,8° ⇒ ∠A = 83,6°

kinderbed(B/2)/2 = 1/(2/√5)

⇒ kinderbed(B/2)/2 = √5/2 ⇒ kinderbed (B/2) = √5

⇒ (B/2) = kinderbed^-1(√5) = 24,1° ⇒ ∠B = 48,2°

kinderbedje (C/2)/2 = 1/(2/√5)

⇒ kinderbed(C/2) = √5 ⇒ (C/2) = kinderbed^-1(√5)

⇒ (C/2) = 24,1° ⇒ ∠C = 48,2°

De hoeken van driehoek ABC zijn dus ∠A = 83,6°, ∠B = 48,2° en ∠C = 48,2°.