Wij kennen een boom is een niet-lineaire datastructuur. Er is geen beperking op het aantal kinderen. AWat is een volledige binaire boom?

Een volledige binaire boom is een speciaal type binaire boom waarbij alle niveaus van de boom volledig gevuld zijn, behalve de knooppunten op het laagste niveau die van zo links mogelijk worden gevuld.

Volledige binaire boom

Enkele terminologie van de volledige binaire boom:

• Wortel – Knooppunt waarin geen rand van de ouder komt. Voorbeeld -knooppunt A
• Kind – Een knooppunt met een inkomende rand wordt een kind genoemd. Voorbeeld: knooppunten B en F zijn respectievelijk het kind van A en C.
• Broer of zus – Knooppunten met dezelfde ouder zijn broers of zussen. Voorbeeld: D en E zijn broers en zussen omdat ze dezelfde ouder B hebben.
• Graad van een knooppunt – Aantal kinderen van een bepaalde ouder. Voorbeeld: Graad van A is 2 en Graad van C is 1. Graad van D is 0.
• Interne/externe knooppunten – Leaf-knooppunten zijn externe knooppunten en niet-bladknooppunten zijn interne knooppunten.
• Niveau – Tel knooppunten in een pad om een ​​bestemmingsknooppunt te bereiken. Voorbeeld: Het niveau van knooppunt D is 2, aangezien knooppunten A en B het pad vormen.
• Hoogte – Aantal randen om het doelknooppunt te bereiken, wortel bevindt zich op hoogte 0. Voorbeeld – Hoogte van knooppunt E is 2 omdat het twee randen vanaf de wortel heeft.

Eigenschappen van volledige binaire boom:

• Van een volledige binaire boom wordt gezegd dat deze een echte binaire boom is, waarbij alle bladeren dezelfde diepte hebben.
• In een volledige binaire boom het aantal knooppunten op diepte D is 2 ^D .
• In een volledige binaire boom met N knooppunten hoogte van de boom is logboek(n+1) .
• Alle niveaus behalve het laatste niveau zijn helemaal vol.

Perfecte binaire boom versus volledige binaire boom:

Een binaire boom met hoogte ‘h’ met het maximale aantal knooppunten is a perfect binaire boom.
Voor een bepaalde hoogte H , is het maximale aantal knooppunten 2 ^u+1 -1 .

A compleet binaire boom met hoogte h is een perfecte binaire boom tot hoogte h-1 , en in het laatste niveau worden de elementen in de volgorde van links naar rechts opgeslagen.

Voorbeeld 1:

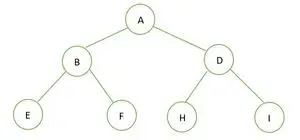
Een binaire boom

De hoogte van de gegeven binaire boom is 2 en het maximale aantal knooppunten in die boom is n= 2^u+1-1 = 2²⁺¹-1 = 2³-1 = 7 .
Daarom kunnen we concluderen dat dit zo is een perfecte binaire boom .
Voor een complete binaire boom is deze vol tot aan de hoogte h-1 d.w.z.; 1, en de laatste niveau-elementen worden in de volgorde van links naar rechts opgeslagen. Daarom is het ook een complete binaire boom. Hier is de weergave van elementen wanneer ze in een array zijn opgeslagen

Element dat niveau voor niveau in een array wordt opgeslagen

In de array worden alle elementen continu opgeslagen.

Voorbeeld 2:

Java is een exemplaar van

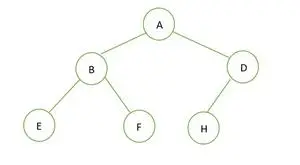
Een binaire boom

De hoogte van de gegeven binaire boom is 2 en het maximale aantal knooppunten dat daar zou moeten zijn, is 2^u+1– 1 = 2²⁺¹– 1 = 2³– 1 = 7 .
Maar het aantal knooppunten in de boom is dat wel 6 . Daarom is het zo geen perfecte binaire boom .
Voor een complete binaire boom is deze vol tot aan de hoogte h-1 d.w.z.; 1 en het laatste niveau-element worden in de volgorde van links naar rechts opgeslagen. Dit is dus een volledige binaire boom . Bewaar het element in een array en het ziet er zo uit;

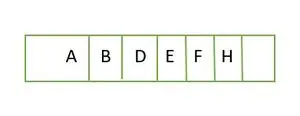
Element dat niveau voor niveau in een array wordt opgeslagen

Voorbeeld 3:

inclusief c-programmering

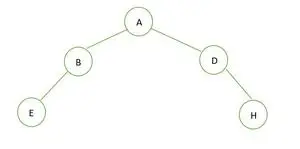
Een binaire boom

De hoogte van de binaire boom is 2 en het maximale aantal knooppunten dat daar kan zijn is 7, maar er zijn slechts 5 knooppunten, dus geen perfecte binaire boom .
In het geval van een volledige binaire boom zien we dat in het laatste niveau de elementen niet van links naar rechts worden gevuld. Zo is het geen volledige binaire boom .

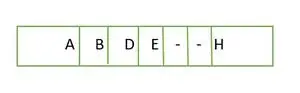
Element dat niveau voor niveau in een array wordt opgeslagen

De elementen in de array zijn niet continu.

Volledige binaire boom versus volledige binaire boom:

Voor een volledige binaire boom heeft elk knooppunt 2 kinderen of 0 kinderen.

Voorbeeld 1:

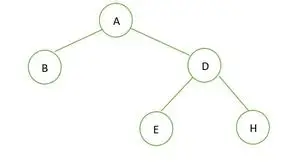
Een binaire boom

In de gegeven binaire boom is er geen knooppunt met graad 1, ofwel 2 of 0 kinderen voor elk knooppunt, daarom is het een volledige binaire boom .

Voor een volledige binaire boom worden de elementen niveau voor niveau opgeslagen en niet vanaf de meest linkse kant in het laatste niveau. Daarom is dit geen volledige binaire boom . De array-weergave is:

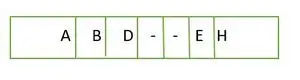
Element dat niveau voor niveau in een array wordt opgeslagen

Voorbeeld 2:

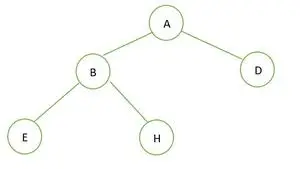
Een binaire boom

In de gegeven binaire boom is er geen knooppunt met graad 1. Elk knooppunt heeft een graad van 2 of 0. Daarom is het een volledige binaire boom .

Voor een volledige binaire boom worden elementen niveau voor niveau opgeslagen en gevuld vanaf de meest linkse kant van het laatste niveau. Vandaar dit A volledige binaire boom . Hieronder ziet u de arrayweergave van de boom:

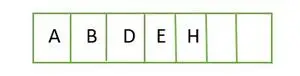
Element dat niveau voor niveau in een array wordt opgeslagen

Voorbeeld 3:

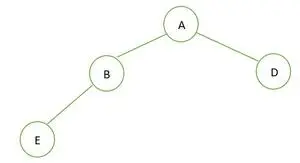
Een binaire boom

In de gegeven binaire boom heeft knooppunt B graad 1, wat in strijd is met de eigenschap van een volledige binaire boom en dat is het ook geen volledige binaire boom

Java-indexvan

Voor een volledige binaire boom worden elementen niveau voor niveau opgeslagen en gevuld vanaf de meest linkse kant van het laatste niveau. Dit is dus een volledige binaire boom . Arrayweergave van de binaire boom is:

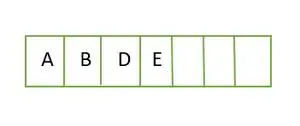
Element dat niveau voor niveau in een array wordt opgeslagen

Voorbeeld 4:

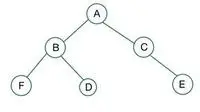
een binaire boom

In de gegeven binaire boom heeft knooppunt C graad 1, wat in strijd is met de eigenschap van een volledige binaire boom en dat is het ook geen volledige binaire boom

Voor een volledige binaire boom worden elementen niveau voor niveau opgeslagen en gevuld vanaf de meest linkse kant van het laatste niveau. Hier schendt knooppunt E de voorwaarde. Daarom is dit geen volledige binaire boom .

Creatie van een volledige binaire boom:

Wij kennen een volledige binaire boom is een boom waarin behalve het laatste niveau (zeg l )al het andere niveau heeft ( 2l ) knooppunten en de knooppunten staan ​​van links naar rechts op een rij.
Het kan worden weergegeven met behulp van een array. Als de ouder het index i dus het linkerkind is bij 2i+1 en het juiste kind is bij 2i+2 .

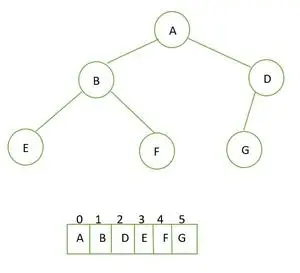
Volledige binaire boom en zijn array-weergave

Algoritme:

Voor het maken van een Volledige binaire boom , we hebben een nodig Stap 1: Initialiseer de root met een nieuw knooppunt als de boom leeg is.

Stap 2: Als de boom niet leeg is, pak dan het voorste element

string.format Java-tekenreeks

• Als het voorste element geen linkerkind heeft, stelt u het linkerkind in op een nieuw knooppunt
• Als het juiste kind niet aanwezig is, stelt u het juiste kind in als nieuw knooppunt

Stap 3: Als het knooppunt beide kinderen heeft, dan knal het uit de wachtrij.

Stap 4: Zet de nieuwe gegevens in de wachtrij.

Illustratie:

Beschouw de onderstaande array:

1. Het eerste element zal de root zijn (waarde bij index = 0 )

A wordt als root genomen

2. Het volgende element (bij index = 1 ) blijft over en het derde element (index = 2 ) zal het rechterkind van root zijn

B als linkerkind en D als rechterkind

3. vierde (index = 3 ) en vijfde element (index = 4 ) zal het linker- en rechterkind zijn van het B-knooppunt

E en F zijn linker- en rechterkind van B

4. Volgend element (index = 5 ) zal een kind van knooppunt D blijven

converteer byte-array naar string

G wordt het linkerkind van het D-knooppunt gemaakt

Dit is hoe een volledige binaire boom wordt gecreëerd.

Implementatie: Voor de implementatie van het bouwen van een complete binaire boom vanaf niveau wordt volgorde-doorgang gegeven deze post .

Toepassing van de volledige binaire boom:

• Hoop sorteren
• Op heap-sortering gebaseerde gegevensstructuur

Controleer of een bepaalde binaire boom compleet is of niet: Volgen deze post om te controleren of de gegeven binaire boom compleet is of niet.