Eerst zullen we de binaire boom En binaire zoekboom afzonderlijk, en dan zullen we kijken naar de verschillen tussen een binaire boom en een binaire zoekboom.

Wat is een binaire boom?

A Binaire boom is eenWijzer naar het linkerkind:Het slaat de referentie van het linkerkindknooppunt op.Wijzer naar het juiste kind:Het slaat de referentie van het rechterkindknooppunt op.Gegevenselement:Het data-element is de waarde van de gegevens die door het knooppunt zijn opgeslagen.

De binaire boom kan worden weergegeven als:

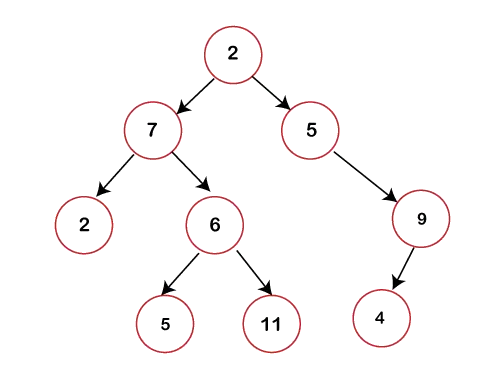
In de bovenstaande figuur kunnen we zien dat elk knooppunt maximaal twee kinderen bevat. Als een knooppunt geen linker- of rechterkind bevat, is de waarde van de aanwijzer met betrekking tot dat kind NULL.

Basisterminologieën die in een binaire boom worden gebruikt, zijn:

Hoofdknooppunt:Het hoofdknooppunt is het eerste of het bovenste knooppunt in een binaire boom.Bovenliggend knooppunt:Wanneer een knooppunt via randen met een ander knooppunt is verbonden, wordt dat knooppunt een ouderknooppunt genoemd. In een binaire boom kan het ouderknooppunt maximaal 2 kinderen hebben.Onderliggend knooppunt:Als een knooppunt zijn voorganger heeft, staat dat knooppunt bekend als a kind knooppunt .Bladknooppunt:Het knooppunt dat geen enkel kind bevat dat bekend staat als a blad knooppunt .Intern knooppunt:Het knooppunt met ten minste twee kinderen, bekend als een interne knooppunt .Diepte van een knooppunt:De afstand van het hoofdknooppunt tot het gegeven knooppunt staat bekend als a diepte van een knooppunt . We bieden labels aan alle knooppunten, zoals het hoofdknooppunt dat is gelabeld met 0 omdat het geen diepte heeft, kinderen van de hoofdknooppunten zijn gelabeld met 1, kinderen van het hoofdknooppunt zijn gelabeld met 2.Hoogte:De langste afstand van het wortelknooppunt tot het bladknooppunt is de hoogte van het knooppunt .

In een binaire boom is er één boom die bekend staat als a perfecte binaire boom . Het is een boom waarin alle interne knooppunten twee knooppunten moeten bevatten en alle bladknooppunten zich op dezelfde diepte moeten bevinden. In het geval van een perfecte binaire boom kan het totale aantal knooppunten in een binaire boom worden berekend met behulp van de volgende vergelijking:

n = 2^m+1-1

waarbij n het aantal knooppunten is, is m de diepte van een knooppunt.

Wat is een binaire zoekboom?

A Binaire zoekboom is een boom die een bepaalde volgorde volgt om de elementen te rangschikken, terwijl de binaire boom geen enkele volgorde volgt. In een binaire zoekboom moet de waarde van het linkerknooppunt kleiner zijn dan het bovenliggende knooppunt, en de waarde van het rechterknooppunt moet groter zijn dan het bovenliggende knooppunt.

Laten we het concept van een binaire zoekboom begrijpen aan de hand van voorbeelden.

In de bovenstaande afbeelding kunnen we zien dat de waarde van het hoofdknooppunt 15 is, wat groter is dan de waarde van alle knooppunten in de linker deelboom. De waarde van het hoofdknooppunt is kleiner dan de waarden van alle knooppunten in een rechtersubboom. Nu gaan we naar het linkerkind van het hoofdknooppunt. 10 is groter dan 8 en kleiner dan 12; het voldoet ook aan de eigenschap van de binaire zoekboom. Nu gaan we naar het rechterkind van het wortelknooppunt; de waarde 20 is groter dan 17 en kleiner dan 25; het voldoet ook aan de eigenschap van een binaire zoekboom. Daarom kunnen we zeggen dat de hierboven weergegeven boom de binaire zoekboom is.

Als we nu de waarde van 12 in 16 in de bovenstaande binaire boom veranderen, moeten we uitzoeken of het nog steeds een binaire zoekboom is of niet.

De waarde van het hoofdknooppunt is 15, wat groter is dan 10 maar kleiner dan 16, en voldoet dus niet aan de eigenschap van de binaire zoekboom. Daarom is het geen binaire zoekboom.

Bewerkingen in de binaire zoekboom

We kunnen invoeg-, verwijder- en zoekbewerkingen uitvoeren op de binaire zoekboom. Laten we begrijpen hoe een zoekopdracht wordt uitgevoerd op een binaire zoekopdracht. Hieronder wordt de binaire boom weergegeven waarop we de zoekbewerking moeten uitvoeren:

Stel dat we 10 moeten zoeken in de bovenstaande binaire boom. Om de binaire zoekopdracht uit te voeren, beschouwen we alle gehele getallen in een gesorteerde array. Eerst maken we een volledige lijst in een zoekruimte, en alle nummers zullen in de zoekruimte voorkomen. De zoekruimte wordt gemarkeerd door twee aanwijzers, d.w.z. begin en einde. De array van de bovenstaande binaire boom kan worden weergegeven als

Eerst berekenen we het middelste element en vergelijken we het middelste element met het element dat moet worden doorzocht. Het middelste element wordt berekend met behulp van n/2. De waarde van n is 7; daarom is het middelste element 15. Het middelste element is niet gelijk aan het gezochte element, d.w.z. 10.

Opmerking: Als het element dat wordt doorzocht kleiner is dan het middenelement, wordt er gezocht in de linkerhelft; anders wordt er op de rechterhelft gezocht. In het geval van gelijkheid wordt het element gevonden.

Omdat het te doorzoeken element kleiner is dan het middenelement, wordt er gezocht op de linkerarray. Nu is de zoekopdracht teruggebracht tot de helft, zoals hieronder weergegeven:

Het middelste element in de linker array is 10, wat gelijk is aan het gezochte element.

Tijdcomplexiteit

Bij een binaire zoekopdracht zijn er n elementen. Als het middelste element niet gelijk is aan het gezochte element, wordt de zoekruimte verkleind tot n/2, en zullen we de zoekruimte met n/2 blijven verkleinen totdat we het element hebben gevonden. Als we bij de hele reductie van n naar n/2 naar n/4 enzovoort gaan, duurt het log₂n stappen.

Verschillen tussen binaire boom en binaire zoekboom