Snelheid is eenvoudigweg de maatstaf voor hoe snel of langzaam een ​​object beweegt, zoals hoe snel je autorijdt. We hebben het hier over een specifiek type snelheid. Hoeksnelheid is alleen een soort snelheid, maar hier moet het lichaam in een cirkelvormig pad bewegen.

Hoeksnelheidsformule

Hoeksnelheid wordt gedefinieerd als de snelheid waarmee de hoekverplaatsing verandert, dat wil zeggen de hoek die een lichaam langs een cirkelvormig pad aflegt. De hoeksnelheid wordt berekend in termen van het aantal rotaties/omwentelingen dat een lichaam maakt in verhouding tot de benodigde tijd. De hoeksnelheid wordt aangegeven met de Griekse letter ‘ω’, bekend als Omega. De SI-eenheid van hoeksnelheid is rad/s.

De hoeksnelheid wordt berekend met behulp van twee verschillende formules,

ω = θ/t ω = v/r

Formule afleiding

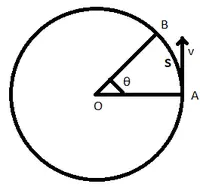
Laten we een lichaam beschouwen dat beweegt in een cirkelvormig pad met straal r, zoals hierboven weergegeven, met een lineaire snelheid v. Laten we veronderstellen dat het lichaam van punt A naar B beweegt, een afstand s door de cirkelboog aflegt en een hoek θ in tijdsperiode t aflegt.

Cirkelvormig pad bedekt door een lichaam

Zoals bekend is de hoeksnelheid de snelheid waarmee de verplaatsing verandert – hoeksnelheid, ω = θ/t

Dus de formule voor hoeksnelheid is ω = θ/t .

Een andere formule voor hoeksnelheid

Ondanks de hierboven genoemde formule is er een andere en breder gebruikte formule voor het berekenen van de hoeksnelheid vanuit het oogpunt van competitieve examens.

Als ω = θ/t ⇢ (1)

Nu weten we dat de afstand die over de boog van een cirkel wordt afgelegd, gelijk is aan de straal maal de afgelegde hoek. Dus,

s = rθ

=> θ = s/r ⇢ (2)

wat is desktop.ini

Van (1) en (2),

ω = s/(rt) ⇢ (3)

Ook vanuit algemeen begrip van lineaire snelheden,

v = s/t ⇢ (4)

Van (3) en (4),

ω = v/r

Voorbeeldproblemen

Vraag 1: Beschouw een lichaam dat beweegt langs een cirkelvormig pad met een straal van 5 meter. Het bestrijkt een halve omwenteling in 5s. Bereken de hoeksnelheid.

Oplossing:

Bij een halve omwenteling is de afgelegde hoek 180 graden. In radialen is het gelijk aan π radialen.

ω = θ/t

=> ω = π/5 = 0,628 rad/s

Vraag 2: Een autowiel met een straal van 2 meter draait met een lineaire snelheid van 10 meter per seconde. Bereken de hoeksnelheid.

Oplossing:

ω = v/r

ω = 10/2

= 5 rad/s

Vraag 3: Beschouw een racewagen die op een cirkelvormige baan rijdt met een snelheid van 18 km/uur en een straal van de baan is 0,2 m. Bereken de hoeksnelheid van de auto.

Oplossing:

v = 18 km/uur = 5 m/s

r = 0,2 meter

ω = v/r

= 5/0,2

= 25 rad/sec

Vraag 4: Een auto beweegt zich langs een cirkelvormige baan met een straal van 2 meter en een hoeksnelheid van 2 rad/s. Bereken de hoek in graden waarover de auto in 2 seconden beweegt.

Oplossing:

Gegeven, ω = 2 rad/s en t = 2s

Omdat ω = θ/t => θ = ωt

=> θ = (2 × 2) = 4 rad

In graden, θ = 4 × (180/π) = 229,18 graden

Vraag 5: Hoeveel omwentelingen heeft een lichaam gemaakt terwijl het zich langs een cirkelvormig pad bewoog met een hoeksnelheid van 7π rad/s in 0,5s?

Oplossing:

Gegeven ω = 7π rad/s en t = 0,5s

Omdat ω = θ/t => θ = ωt

θ = (7π × 0,5) = 3,5π

In 2π rad is het aantal afgelegde omwentelingen 1

=> In 1 rad is het afgelegde toerental (1/2π)

=> In 3,5π rad, omwentelingen = 3,5π/2π = 1,75 omwentelingen

Het lichaam zal dus 1 volledige omwenteling en 3/4 van de volgende omwenteling voltooien in een tijdsperiode van 0,5 s.

Vraag 6: Wat zal de hoeksnelheid zijn van een lichaam dat beweegt in een cirkelvormige baan met een straal van 2 m die 4 m booglengte 5s beslaat.

Oplossing:

Gegeven s = 4m, r = 2m, t = 5s

Met formule s = rθ => θ = s/r

θ = 4/2 = 2 rad

Aangezien ω = θ/t

retourneert een array-Java

=> ω = 2/5 = 0,4 rad/s