Een prisma is een driedimensionale vaste figuur met twee identieke uiteinden. Het bestaat uit vlakke zijden, soortgelijke bases en gelijke doorsneden. De vlakken zijn parallellogrammen of rechthoeken zonder basis. Een dergelijk prisma met drie rechthoekige vlakken en twee evenwijdige driehoekige bases wordt een driehoekig prisma genoemd. De driehoekige basissen zijn verbonden door zijvlakken die evenwijdig aan elkaar lopen.

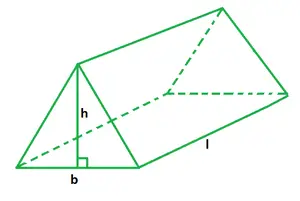
Volume van een driehoekige prismaformule

Het volume van een driehoekig prisma wordt gedefinieerd als de ruimte erin of de ruimte die erdoor wordt gevuld. Het kennen van het basisoppervlak en de hoogte van een driehoekig prisma is alles wat nodig is om het volume ervan te berekenen. Het volume van een driehoekig prisma is gelijk aan het product van het oppervlak van de basis en de hoogte van het prisma, ook wel de lengte van het prisma genoemd. Het basisoppervlak van een driehoekig prisma is gelijk aan de helft van het product van de driehoekige basis en zijn hoogte.

Formule

V = (1/2) × b × h × l

waar,

b is de driehoekige basis,

h is de hoogte van het prisma,

l is de lengte van het prisma.

Voorbeeldproblemen

Probleem 1. Bepaal het volume van een driehoekig prisma als de basis 6 cm is, de hoogte 8 cm en de lengte 12 cm.

Oplossing:

We hebben b = 6, h = 8 en l = 12.

rr-algoritme

Met behulp van de formule die we hebben,

V = (1/2) × b × h × l

= (1/2) × 6 × 8 × 12

= 3×8×12

= 288 cu. cm

Probleem 2. Bepaal het volume van een driehoekig prisma als de basis 5 cm is, de hoogte 7 cm en de lengte 8 cm.

Oplossing:

We hebben b = 5, h = 7 en l = 8.

Met behulp van de formule die we hebben,

V = (1/2) × b × h × l

= (1/2) × 5 × 7 × 8

= 5×7×4

teken naar int java

= 140 cu. cm

Probleem 3. Zoek de lengte van het driehoekige prisma als de basis 6 cm is, de hoogte 9 cm en het volume 98 cu. cm.

Oplossing:

We hebben b = 6, h = 9 en V = 98.

Met behulp van de formule die we hebben,

V = (1/2) × b × h × l

=> 98 = (1/2) × 6 × 9 × l

snaar omkeren in c

=> 196 = 27l

=> l=196/27

=> l= 7,25 cm

Probleem 4. Bepaal de hoogte van het driehoekige prisma als de basis 8 cm is, de lengte 14 cm en het volume 504 cu. cm.

Oplossing:

We hebben b = 8, l = 14 en V = 504.

Met behulp van de formule die we hebben,

V = (1/2) × b × h × l

=> 504 = (1/2) × 8 × h × 14

=> 504 = 56 uur

=> h = 504/56

=> h = 9 cm

Probleem 5. Bepaal de oppervlakte van de basis van het driehoekige prisma als de lengte 18 cm is, de hoogte 10 cm en het volume 450 cu. cm.

Oplossing:

We hebben l = 18, h = 10 en V = 450.

Met behulp van de formule voor volume die we hebben,

V = (1/2) × b × h × l

=> 450 = (1/2) × b × 10 × 18

=> 450 = 90b

=> b = 450/90

=> b = 5 cm

als het anders in Java is

Daarom is het gebied van de driehoekige basis:

A = (1/2) × b × h

= (1/2) × 5 × 10

= 25 vierkante cm