Volume van een bol is de hoeveelheid vloeistof die een bol kan bevatten. De formule voor het volume van de bol wordt gegeven als 4/3πr³. Het is de ruimte die wordt ingenomen door een bol in de driedimensionale ruimte. Het wordt gemeten in eenheid³dat wil zeggen m³, cm³, enz. Een bol is een driedimensionaal vast object met een ronde vorm in de geometrie.

Het volume van de bol is de totale ruimte die wordt ingenomen door het oppervlak van de bol en is evenredig met de derde macht van de straal van de bol. In dit artikel zullen we in detail leren over Volume of Sphere, Volume of Sphere-formule, Volume of Sphere-formulevoorbeelden en andere.

• Wat is het volume van een bol?
• Volume van bolformule
• Volume van een vaste bol
• Volume van een holle bol
• Volume van bolformule-afleiding
• Hoe het volume van de bol berekenen?

Wat is het volume van een bol?

Het volume van een bol is de hoeveelheid ruimte die deze inneemt. De bol is een driedimensionale ronde vaste vorm waarin alle punten op het oppervlak op gelijke afstand van het midden liggen. De vaste afstand is de straal van de bol en het vaste punt is het middelpunt van de bol. We zullen een vormverandering opmerken wanneer de cirkel wordt omgedraaid. Als resultaat van de rotatie van het tweedimensionale object dat bekend staat als een cirkel, wordt de driedimensionale vorm van een bol verkregen.

Kom meer te weten,

• Gebied
• Oppervlakte van bol

Volume van een boldefinitie

Het volume van een bol is de totale massa omsloten door het oppervlak van de bol. Het is de 3D-ruimte binnen de bol. Het hangt af van de straal van de bol. De onderstaande afbeelding toont een bol met straal r en het volume ervan.

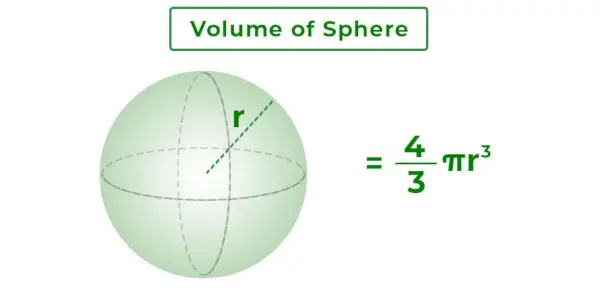
Volume van bolformule

Volume van bolformule is de formule die wordt gebruikt om het volume van de bol te vinden wanneer de straal wordt gegeven. Het volume van de bolformule voor de bol met straal R wordt hieronder toegevoegd,

Volume van bolformule = 4/3πr ³

Waar,

• R is de straal van een bol
• Pi is een constante en de waarde ervan is 22/7

Een bol wordt over het algemeen onderverdeeld in twee, namelijk:

• Volume van vaste bol
• Volume van holle bol

Laten we ze in detail leren kennen.

Volume van een vaste bol

Een massieve bol is een bol die tot binnenin volledig gevuld is. dat wil zeggen, het heeft massa tot aan de kern en de formule voor het volume wanneer de straal r is,

Volume van een massieve bol(V) = (4/3)πr ³

Volume van een holle bol

Voor een holle bol is de interne ruimte leeg en stel dat de buitenste straal dat ook is R en de binnenradius is R, vervolgens wordt het volume berekend met behulp van de formule,

Volume van holle bol = (4/3)π(R ³ - R ³ )

Volume van bolformule-afleiding

Het volume van de bolformule kan worden afgeleid met behulp van de volgende methoden:

• Integratie gebruiken
• Met behulp van Archimedes Relatie tussen cilinder, kegel en bol

Laten we deze methoden als volgt in detail bespreken:

Volume van bol met behulp van integratie

Met behulp van de integratiebenadering kunnen we eenvoudig het volume van een bol berekenen.

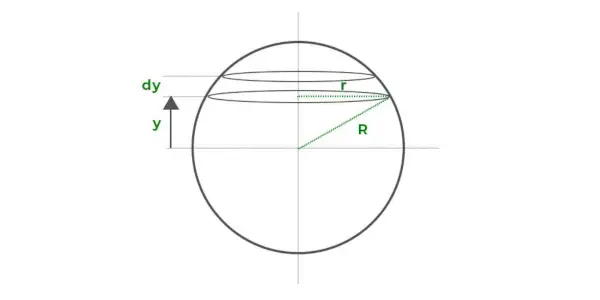
Stel dat het volume van de bol bestaat uit een reeks dunne ronde schijven die op elkaar zijn gestapeld, zoals weergegeven in het diagram hierboven. Elke dunne schijf heeft een straal r en een dikte van dy die op de y-afstand van de x-as ligt.

Stel dat het volume van een schijf dV is. De waarde van dV wordt gegeven door,

dV = (πr²) Jij

Dus dV = π (R²- En²) Jij

Het totale volume van de bol zal de som zijn van de volumes van al deze kleine schijven. De vereiste waarde kan worden verkregen door de uitdrukking van limiet -R tot R te integreren.

Dus het volume van de bol wordt,

V =int_{y=-R}^{y=R} dV

⇒ V =int_{y=-R}^{y=R}π(R^2 – y^2)dy

⇒ V =pi|(R^2y – frac{y^3}{3})dy|_{y=-R}^{y=R}

⇒ V =pi left[R^3-frac{R^3}{3}-(-R^3+frac{R^3}{3}) ight]

⇒ V =pi left[2R^3-frac{2R^3}{3} ight]

⇒ V =frac{4}{3}pi R^3

Zo wordt de formule voor het volume van de bol afgeleid.

Volume van bol met behulp van Archimedes-relaties

Zoals Archimedes al heeft bewezen: als een kegel, een bol en een cilinder dezelfde straal r en dezelfde hoogte hebben, hebben hun volumes een verhouding van 1:2:3.

Daarom kunnen we zeggen:

Volume van cilinder = volume van kegel + volume van bol

Dus volume van bol = volume van cilinder – volume van kegel

Zoals we weten is dat cilindervolume = πr²h en volume van de kegel = (1/3)πr²H

Als we deze waarden in de vergelijking invullen, krijgen we:

Volume van bol = πr²h – (1/3)πr²h = (2/3)πr²H

We nemen aan dat de hoogte van de cilinder gelijk is aan de diameter van de bol, namelijk 2r. Dus:

Het volume van de bol is (2/3)πr ² h = (2/3)πr ² (2r) = (4/3)πr ³

Controleer ook

• Bolvormige dopvolumeformule
• Sferische sectorformule
• Sferische segmentformule

Hoe het volume van de bol berekenen?

Het bolvolume is de ruimte die door een bol wordt ingenomen. Het volume kan worden berekend met behulp van de formule V = 4/3πr ³ .

De stappen die nodig zijn om het volume van een bol te berekenen zijn:

Stap 1: Markeer de waarde van de straal van de bol.

2 september: Zoek de kubus van de straal.

Stap 3: Vermenigvuldig de derde macht van de straal met (4/3)π

Stap 4: Voeg de (eenheid) toe³naar het uiteindelijke antwoord.

Voorbeeld om het volume van de bol te berekenen

Voorbeeld: Zoek het volume van een bol met een straal van 7 cm.

Gegeven, r = 7 cm

V = (4/3)πr³

Volume van bol, V = ((4/3) × π × 7³) cm³

Hoogte = 1436,8 cm³

Het volume van de bol is dus 1436,8 cm³

Lees verder

• Volume van kegel
• Volume van kubus
• Volume van cilinder

Volume van bolvoorbeelden

Voorbeeld 1. Zoek het volume van de bol met een straal van 9 cm.

Oplossing:

Wij hebben, r = 9

Bolvolume = 4/3 πr³

⇒ Bolvolume = (4/3) (3,14) (9) (9) (9)

⇒ Volume van bol = (4) (3,14) (3) (9) (9)

⇒ Inhoud bol = 3052 cm³

Voorbeeld 2. Zoek het volume van de bol met een straal van 12 cm.

Oplossing:

Wij hebben, r = 12

Bolvolume = 4/3 πr³

⇒ Bolvolume = (4/3) (3,14) (12) (12) (12)

⇒ Volume van bol = (4) (3,14) (4) (12) (12)

⇒ Volume bol = 7234,56 cm³

Voorbeeld 3. Zoek het volume van de bol met een straal van 6 cm.

Oplossing:

Wij hebben, r = 6

Bolvolume = 4/3 πr³

⇒ Bolvolume = (4/3) (3,14) (6) (6) (6)

⇒ Volume van bol = (4) (3,14) (2) (6) (6)

⇒ Volume bol = 904,32 cm³

Voorbeeld 4. Zoek het volume van de bol met een straal van 4 cm.

Oplossing:

Wij hebben, r = 4

Bolvolume = 4/3 πr3

⇒ Bolvolume = (4/3) (3,14) (4) (4) (4)

⇒ Volume van bol = (1,33) (3,14) (4) (4) (4)

⇒ Volume bol = 267,27 cm³

Voorbeeld 5. Zoek het volume van de bol met een diameter van 10 cm.

Oplossing:

Wij hebben, 2r = 10

zwevende css

⇒ r = 5

Volume van bol = 4/3 πr³

⇒ Bolvolume = (4/3) (3,14) (5) (5) (5)

⇒ Volume van bol = (1,33) (3,14) (5) (5) (5)

⇒ Volume bol = 522,025 cm³

Voorbeeld 6. Zoek het volume van de bol met een diameter van 16 cm.

Oplossing:

Wij hebben, 2r = 16

⇒ r = 8

Bolvolume = 4/3 πr³

⇒ Bolvolume = (4/3) (3,14) (8) (8) (8)

⇒ Volume van bol = (1,33) (3,14) (8) (8) (8)

⇒ Volume bol = 2138,21 cm³

Voorbeeld 7. Zoek het volume van de bol met een diameter van 14 cm.

Oplossing:

Wij hebben, 2r = 14

⇒ r = 7

Bolvolume = 4/3 πr³

⇒ Bolvolume = (4/3) (3,14) (7) (7) (7)

⇒ Volume van bol = (1,33) (3,14) (7) (7) (7)

⇒ Volume bol = 1432,43 cm³

Volume met sfeeroefeningsvragen

Vraag 1: Zoek het volume van de bol met een diameter van 34 cm.

Vraag 2: Zoek het volume van de holle bol waarvan de binnenstraal 4 cm is en de buitenstraal 8 cm.

Vraag 3: Zoek het volume van de bol waarvan de straal 14 cm is.

Vraag 4: Wat is het volume van een bol waarvan de straal gelijk is aan de zijde van een vierkant met een oppervlakte van 144 m².

Volume van Sphere-FAQ's

Wat is bolvolume?

Het volume van de bol is de ruimte die wordt ingenomen door het oppervlak van de bol.

Wat is de oppervlakte van een bolformule?

Totale oppervlakte van bol met straal r is, Oppervlakte = 4πr ²

Wat is de formule voor het volume van een bol?

Volume van een bol met straal r is, Volume = 4/3πr ³

Hoe vinden we het volume van het halfrond?

Volume van een halve bol met straal r is, Volume = 2/3πr ³

Wat is de verhouding tussen het volume van bol en halfrond?

Als een bol en een halve bol dezelfde stralen hebben, is de verhouding van hun volume:

IN ₁ : IN ₂ = (4/3πr ³ ) : (2/3πr ³ ) = 2 : 1

Wat is de volume-eenheid van een bol?

Het volume van de bol wordt gemeten in m³, cm³, liter, enz. M ³ is de standaard meeteenheid.

Wat is het bolvolume als de straal gehalveerd is?

Bolvolume = (4/3)πr³= (4/3)π(r/2)³= (4/3)π(r³/8) = Volume/8. Het volume van de bol wordt dus een achtste.