Voorwaarde - Fenwick-boom
We weten dat het beantwoorden van bereiksomquery's op een 1-D-array efficiënt binair geïndexeerde boom (of Fenwick Tree) de beste keuze is (zelfs beter dan een segmentboom vanwege minder geheugenvereisten en iets sneller dan een segmentboom).
Kunnen we submatrixsomvragen efficiënt beantwoorden met behulp van Binary Indexed Tree?
Het antwoord is Ja . Dit is mogelijk met behulp van een 2D BIT wat niets anders is dan een array van 1D BIT.
tekenreeksaaneenschakeling java
Algoritme:
We beschouwen het onderstaande voorbeeld. Stel dat we de som van alle getallen binnen het gemarkeerde gebied moeten vinden:
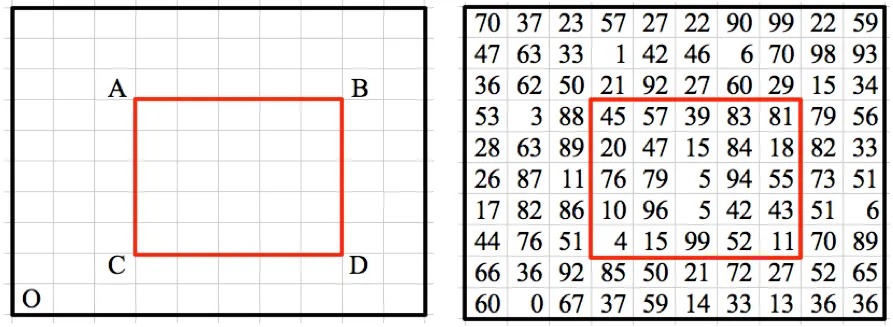
We gaan uit van de oorsprong van de matrix onderaan - O. Dan maakt een 2D BIT gebruik van het feit dat-
Java-anonieme functie
Sum under the marked area = Sum(OB) - Sum(OD) - Sum(OA) + Sum(OC) 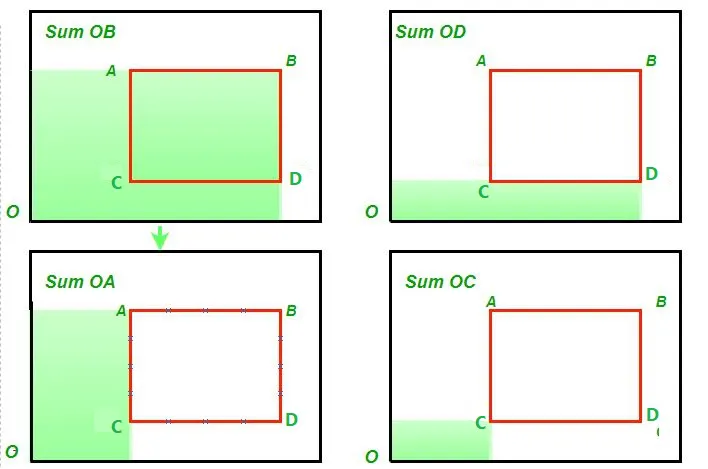
In ons programma gebruiken we de functie getSum(xy) die de som van de matrix van (0 0) tot (xy) vindt.
Vandaar onderstaande formule:
Sum under the marked area = Sum(OB) - Sum(OD) - Sum(OA) + Sum(OC) The above formula gets reduced to Query(x1y1x2y2) = getSum(x2 y2) - getSum(x2 y1-1) - getSum(x1-1 y2) + getSum(x1-1 y1-1) waar
x1 j1 = x- en y-coördinaten van C
x2 j2 = x- en y-coördinaten van B
De functie updateBIT(xy val) werkt alle elementen onder de regio bij – (xy) tot (NM) waar
N = maximale X-coördinaat van de hele matrix.
M = maximale Y-coördinaat van de hele matrix.
De restprocedure lijkt veel op die van 1D Binary Indexed Tree.
Hieronder vindt u de C++-implementatie van een 2D-geïndexeerde boom
C++/* C++ program to implement 2D Binary Indexed Tree 2D BIT is basically a BIT where each element is another BIT. Updating by adding v on (x y) means it's effect will be found throughout the rectangle [(x y) (max_x max_y)] and query for (x y) gives you the result of the rectangle [(0 0) (x y)] assuming the total rectangle is [(0 0) (max_x max_y)]. So when you query and update on this BITyou have to be careful about how many times you are subtracting a rectangle and adding it. Simple set union formula works here. So if you want to get the result of a specific rectangle [(x1 y1) (x2 y2)] the following steps are necessary: Query(x1y1x2y2) = getSum(x2 y2)-getSum(x2 y1-1) - getSum(x1-1 y2)+getSum(x1-1 y1-1) Here 'Query(x1y1x2y2)' means the sum of elements enclosed in the rectangle with bottom-left corner's co-ordinates (x1 y1) and top-right corner's co-ordinates - (x2 y2) Constraints -> x1<=x2 and y1<=y2 / y | | --------(x2y2) | | | | | | | | | | --------- | (x1y1) | |___________________________ (0 0) x--> In this program we have assumed a square matrix. The program can be easily extended to a rectangular one. */ #include
/* Java program to implement 2D Binary Indexed Tree 2D BIT is basically a BIT where each element is another BIT. Updating by adding v on (x y) means it's effect will be found throughout the rectangle [(x y) (max_x max_y)] and query for (x y) gives you the result of the rectangle [(0 0) (x y)] assuming the total rectangle is [(0 0) (max_x max_y)]. So when you query and update on this BITyou have to be careful about how many times you are subtracting a rectangle and adding it. Simple set union formula works here. So if you want to get the result of a specific rectangle [(x1 y1) (x2 y2)] the following steps are necessary: Query(x1y1x2y2) = getSum(x2 y2)-getSum(x2 y1-1) - getSum(x1-1 y2)+getSum(x1-1 y1-1) Here 'Query(x1y1x2y2)' means the sum of elements enclosed in the rectangle with bottom-left corner's co-ordinates (x1 y1) and top-right corner's co-ordinates - (x2 y2) Constraints -> x1<=x2 and y1<=y2 / y | | --------(x2y2) | | | | | | | | | | --------- | (x1y1) | |___________________________ (0 0) x--> In this program we have assumed a square matrix. The program can be easily extended to a rectangular one. */ class GFG { static final int N = 4; // N-.max_x and max_y // A structure to hold the queries static class Query { int x1 y1; // x and y co-ordinates of bottom left int x2 y2; // x and y co-ordinates of top right public Query(int x1 int y1 int x2 int y2) { this.x1 = x1; this.y1 = y1; this.x2 = x2; this.y2 = y2; } }; // A function to update the 2D BIT static void updateBIT(int BIT[][] int x int y int val) { for (; x <= N; x += (x & -x)) { // This loop update all the 1D BIT inside the // array of 1D BIT = BIT[x] for (; y <= N; y += (y & -y)) BIT[x][y] += val; } return; } // A function to get sum from (0 0) to (x y) static int getSum(int BIT[][] int x int y) { int sum = 0; for(; x > 0; x -= x&-x) { // This loop sum through all the 1D BIT // inside the array of 1D BIT = BIT[x] for(; y > 0; y -= y&-y) { sum += BIT[x][y]; } } return sum; } // A function to create an auxiliary matrix // from the given input matrix static void constructAux(int mat[][] int aux[][]) { // Initialise Auxiliary array to 0 for (int i = 0; i <= N; i++) for (int j = 0; j <= N; j++) aux[i][j] = 0; // Construct the Auxiliary Matrix for (int j = 1; j <= N; j++) for (int i = 1; i <= N; i++) aux[i][j] = mat[N - j][i - 1]; return; } // A function to construct a 2D BIT static void construct2DBIT(int mat[][] int BIT[][]) { // Create an auxiliary matrix int [][]aux = new int[N + 1][N + 1]; constructAux(mat aux); // Initialise the BIT to 0 for (int i = 1; i <= N; i++) for (int j = 1; j <= N; j++) BIT[i][j] = 0; for (int j = 1; j <= N; j++) { for (int i = 1; i <= N; i++) { // Creating a 2D-BIT using update function // everytime we/ encounter a value in the // input 2D-array int v1 = getSum(BIT i j); int v2 = getSum(BIT i j - 1); int v3 = getSum(BIT i - 1 j - 1); int v4 = getSum(BIT i - 1 j); // Assigning a value to a particular element // of 2D BIT updateBIT(BIT i j aux[i][j] - (v1 - v2 - v4 + v3)); } } return; } // A function to answer the queries static void answerQueries(Query q[] int m int BIT[][]) { for (int i = 0; i < m; i++) { int x1 = q[i].x1 + 1; int y1 = q[i].y1 + 1; int x2 = q[i].x2 + 1; int y2 = q[i].y2 + 1; int ans = getSum(BIT x2 y2) - getSum(BIT x2 y1 - 1) - getSum(BIT x1 - 1 y2) + getSum(BIT x1 - 1 y1 - 1); System.out.printf('Query(%d %d %d %d) = %dn' q[i].x1 q[i].y1 q[i].x2 q[i].y2 ans); } return; } // Driver Code public static void main(String[] args) { int mat[][] = { {1 2 3 4} {5 3 8 1} {4 6 7 5} {2 4 8 9} }; // Create a 2D Binary Indexed Tree int [][]BIT = new int[N + 1][N + 1]; construct2DBIT(mat BIT); /* Queries of the form - x1 y1 x2 y2 For example the query- {1 1 3 2} means the sub-matrix- y / 3 | 1 2 3 4 Sub-matrix 2 | 5 3 8 1 {1132} --. 3 8 1 1 | 4 6 7 5 6 7 5 0 | 2 4 8 9 | --|------ 0 1 2 3 ---. x | Hence sum of the sub-matrix = 3+8+1+6+7+5 = 30 */ Query q[] = {new Query(1 1 3 2) new Query(2 3 3 3) new Query(1 1 1 1)}; int m = q.length; answerQueries(q m BIT); } } // This code is contributed by 29AjayKumar
'''Python3 program to implement 2D Binary Indexed Tree 2D BIT is basically a BIT where each element is another BIT. Updating by adding v on (x y) means it's effect will be found throughout the rectangle [(x y) (max_x max_y)] and query for (x y) gives you the result of the rectangle [(0 0) (x y)] assuming the total rectangle is [(0 0) (max_x max_y)]. So when you query and update on this BITyou have to be careful about how many times you are subtracting a rectangle and adding it. Simple set union formula works here. So if you want to get the result of a specific rectangle [(x1 y1) (x2 y2)] the following steps are necessary: Query(x1y1x2y2) = getSum(x2 y2)-getSum(x2 y1-1) - getSum(x1-1 y2)+getSum(x1-1 y1-1) Here 'Query(x1y1x2y2)' means the sum of elements enclosed in the rectangle with bottom-left corner's co-ordinates (x1 y1) and top-right corner's co-ordinates - (x2 y2) Constraints -> x1<=x2 and y1<=y2 / y | | --------(x2y2) | | | | | | | | | | --------- | (x1y1) | |___________________________ (0 0) x--> In this program we have assumed a square matrix. The program can be easily extended to a rectangular one. ''' N = 4 # N-.max_x and max_y # A structure to hold the queries class Query: def __init__(self x1y1x2y2): self.x1 = x1; self.y1 = y1; self.x2 = x2; self.y2 = y2; # A function to update the 2D BIT def updateBIT(BITxyval): while x <= N: # This loop update all the 1D BIT inside the # array of 1D BIT = BIT[x] while y <= N: BIT[x][y] += val; y += (y & -y) x += (x & -x) return; # A function to get sum from (0 0) to (x y) def getSum(BITxy): sum = 0; while x > 0: # This loop sum through all the 1D BIT # inside the array of 1D BIT = BIT[x] while y > 0: sum += BIT[x][y]; y -= y&-y x -= x&-x return sum; # A function to create an auxiliary matrix # from the given input matrix def constructAux(mataux): # Initialise Auxiliary array to 0 for i in range(N + 1): for j in range(N + 1): aux[i][j] = 0 # Construct the Auxiliary Matrix for j in range(1 N + 1): for i in range(1 N + 1): aux[i][j] = mat[N - j][i - 1]; return # A function to construct a 2D BIT def construct2DBIT(matBIT): # Create an auxiliary matrix aux = [None for i in range(N + 1)] for i in range(N + 1) : aux[i]= [None for i in range(N + 1)] constructAux(mat aux) # Initialise the BIT to 0 for i in range(1 N + 1): for j in range(1 N + 1): BIT[i][j] = 0; for j in range(1 N + 1): for i in range(1 N + 1): # Creating a 2D-BIT using update function # everytime we/ encounter a value in the # input 2D-array v1 = getSum(BIT i j); v2 = getSum(BIT i j - 1); v3 = getSum(BIT i - 1 j - 1); v4 = getSum(BIT i - 1 j); # Assigning a value to a particular element # of 2D BIT updateBIT(BIT i j aux[i][j] - (v1 - v2 - v4 + v3)); return; # A function to answer the queries def answerQueries(qmBIT): for i in range(m): x1 = q[i].x1 + 1; y1 = q[i].y1 + 1; x2 = q[i].x2 + 1; y2 = q[i].y2 + 1; ans = getSum(BIT x2 y2) - getSum(BIT x2 y1 - 1) - getSum(BIT x1 - 1 y2) + getSum(BIT x1 - 1 y1 - 1); print('Query (' q[i].x1 ' ' q[i].y1 ' ' q[i].x2 ' ' q[i].y2 ') = ' ans sep = '') return; # Driver Code mat= [[1 2 3 4] [5 3 8 1] [4 6 7 5] [2 4 8 9]]; # Create a 2D Binary Indexed Tree BIT = [None for i in range(N + 1)] for i in range(N + 1): BIT[i]= [None for i in range(N + 1)] for j in range(N + 1): BIT[i][j]=0 construct2DBIT(mat BIT); ''' Queries of the form - x1 y1 x2 y2 For example the query- {1 1 3 2} means the sub-matrix- y / 3 | 1 2 3 4 Sub-matrix 2 | 5 3 8 1 {1132} --. 3 8 1 1 | 4 6 7 5 6 7 5 0 | 2 4 8 9 | --|------ 0 1 2 3 ---. x | Hence sum of the sub-matrix = 3+8+1+6+7+5 = 30 ''' q = [Query(1 1 3 2) Query(2 3 3 3) Query(1 1 1 1)]; m = len(q) answerQueries(q m BIT); # This code is contributed by phasing17
/* C# program to implement 2D Binary Indexed Tree 2D BIT is basically a BIT where each element is another BIT. Updating by.Adding v on (x y) means it's effect will be found throughout the rectangle [(x y) (max_x max_y)] and query for (x y) gives you the result of the rectangle [(0 0) (x y)] assuming the total rectangle is [(0 0) (max_x max_y)]. So when you query and update on this BITyou have to be careful about how many times you are subtracting a rectangle and.Adding it. Simple set union formula works here. So if you want to get the result of a specific rectangle [(x1 y1) (x2 y2)] the following steps are necessary: Query(x1y1x2y2) = getSum(x2 y2)-getSum(x2 y1-1) - getSum(x1-1 y2)+getSum(x1-1 y1-1) Here 'Query(x1y1x2y2)' means the sum of elements enclosed in the rectangle with bottom-left corner's co-ordinates (x1 y1) and top-right corner's co-ordinates - (x2 y2) Constraints -> x1<=x2 and y1<=y2 / y | | --------(x2y2) | | | | | | | | | | --------- | (x1y1) | |___________________________ (0 0) x--> In this program we have assumed a square matrix. The program can be easily extended to a rectangular one. */ using System; class GFG { static readonly int N = 4; // N-.max_x and max_y // A structure to hold the queries public class Query { public int x1 y1; // x and y co-ordinates of bottom left public int x2 y2; // x and y co-ordinates of top right public Query(int x1 int y1 int x2 int y2) { this.x1 = x1; this.y1 = y1; this.x2 = x2; this.y2 = y2; } }; // A function to update the 2D BIT static void updateBIT(int []BIT int x int y int val) { for (; x <= N; x += (x & -x)) { // This loop update all the 1D BIT inside the // array of 1D BIT = BIT[x] for (; y <= N; y += (y & -y)) BIT[xy] += val; } return; } // A function to get sum from (0 0) to (x y) static int getSum(int []BIT int x int y) { int sum = 0; for(; x > 0; x -= x&-x) { // This loop sum through all the 1D BIT // inside the array of 1D BIT = BIT[x] for(; y > 0; y -= y&-y) { sum += BIT[x y]; } } return sum; } // A function to create an auxiliary matrix // from the given input matrix static void constructAux(int []mat int []aux) { // Initialise Auxiliary array to 0 for (int i = 0; i <= N; i++) for (int j = 0; j <= N; j++) aux[i j] = 0; // Construct the Auxiliary Matrix for (int j = 1; j <= N; j++) for (int i = 1; i <= N; i++) aux[i j] = mat[N - j i - 1]; return; } // A function to construct a 2D BIT static void construct2DBIT(int []mat int []BIT) { // Create an auxiliary matrix int []aux = new int[N + 1 N + 1]; constructAux(mat aux); // Initialise the BIT to 0 for (int i = 1; i <= N; i++) for (int j = 1; j <= N; j++) BIT[i j] = 0; for (int j = 1; j <= N; j++) { for (int i = 1; i <= N; i++) { // Creating a 2D-BIT using update function // everytime we/ encounter a value in the // input 2D-array int v1 = getSum(BIT i j); int v2 = getSum(BIT i j - 1); int v3 = getSum(BIT i - 1 j - 1); int v4 = getSum(BIT i - 1 j); // Assigning a value to a particular element // of 2D BIT updateBIT(BIT i j aux[ij] - (v1 - v2 - v4 + v3)); } } return; } // A function to answer the queries static void answerQueries(Query []q int m int []BIT) { for (int i = 0; i < m; i++) { int x1 = q[i].x1 + 1; int y1 = q[i].y1 + 1; int x2 = q[i].x2 + 1; int y2 = q[i].y2 + 1; int ans = getSum(BIT x2 y2) - getSum(BIT x2 y1 - 1) - getSum(BIT x1 - 1 y2) + getSum(BIT x1 - 1 y1 - 1); Console.Write('Query({0} {1} {2} {3}) = {4}n' q[i].x1 q[i].y1 q[i].x2 q[i].y2 ans); } return; } // Driver Code public static void Main(String[] args) { int []mat = { {1 2 3 4} {5 3 8 1} {4 6 7 5} {2 4 8 9} }; // Create a 2D Binary Indexed Tree int []BIT = new int[N + 1N + 1]; construct2DBIT(mat BIT); /* Queries of the form - x1 y1 x2 y2 For example the query- {1 1 3 2} means the sub-matrix- y / 3 | 1 2 3 4 Sub-matrix 2 | 5 3 8 1 {1132} --. 3 8 1 1 | 4 6 7 5 6 7 5 0 | 2 4 8 9 | --|------ 0 1 2 3 ---. x | Hence sum of the sub-matrix = 3+8+1+6+7+5 = 30 */ Query []q = {new Query(1 1 3 2) new Query(2 3 3 3) new Query(1 1 1 1)}; int m = q.Length; answerQueries(q m BIT); } } // This code is contributed by Rajput-Ji
<script> /* Javascript program to implement 2D Binary Indexed Tree 2D BIT is basically a BIT where each element is another BIT. Updating by adding v on (x y) means it's effect will be found throughout the rectangle [(x y) (max_x max_y)] and query for (x y) gives you the result of the rectangle [(0 0) (x y)] assuming the total rectangle is [(0 0) (max_x max_y)]. So when you query and update on this BITyou have to be careful about how many times you are subtracting a rectangle and adding it. Simple set union formula works here. So if you want to get the result of a specific rectangle [(x1 y1) (x2 y2)] the following steps are necessary: Query(x1y1x2y2) = getSum(x2 y2)-getSum(x2 y1-1) - getSum(x1-1 y2)+getSum(x1-1 y1-1) Here 'Query(x1y1x2y2)' means the sum of elements enclosed in the rectangle with bottom-left corner's co-ordinates (x1 y1) and top-right corner's co-ordinates - (x2 y2) Constraints -> x1<=x2 and y1<=y2 / y | | --------(x2y2) | | | | | | | | | | --------- | (x1y1) | |___________________________ (0 0) x--> In this program we have assumed a square matrix. The program can be easily extended to a rectangular one. */ let N = 4; // N-.max_x and max_y // A structure to hold the queries class Query { constructor(x1y1x2y2) { this.x1 = x1; this.y1 = y1; this.x2 = x2; this.y2 = y2; } } // A function to update the 2D BIT function updateBIT(BITxyval) { for (; x <= N; x += (x & -x)) { // This loop update all the 1D BIT inside the // array of 1D BIT = BIT[x] for (; y <= N; y += (y & -y)) BIT[x][y] += val; } return; } // A function to get sum from (0 0) to (x y) function getSum(BITxy) { let sum = 0; for(; x > 0; x -= x&-x) { // This loop sum through all the 1D BIT // inside the array of 1D BIT = BIT[x] for(; y > 0; y -= y&-y) { sum += BIT[x][y]; } } return sum; } // A function to create an auxiliary matrix // from the given input matrix function constructAux(mataux) { // Initialise Auxiliary array to 0 for (let i = 0; i <= N; i++) for (let j = 0; j <= N; j++) aux[i][j] = 0; // Construct the Auxiliary Matrix for (let j = 1; j <= N; j++) for (let i = 1; i <= N; i++) aux[i][j] = mat[N - j][i - 1]; return; } // A function to construct a 2D BIT function construct2DBIT(matBIT) { // Create an auxiliary matrix let aux = new Array(N + 1); for(let i=0;i<(N+1);i++) { aux[i]=new Array(N+1); } constructAux(mat aux); // Initialise the BIT to 0 for (let i = 1; i <= N; i++) for (let j = 1; j <= N; j++) BIT[i][j] = 0; for (let j = 1; j <= N; j++) { for (let i = 1; i <= N; i++) { // Creating a 2D-BIT using update function // everytime we/ encounter a value in the // input 2D-array let v1 = getSum(BIT i j); let v2 = getSum(BIT i j - 1); let v3 = getSum(BIT i - 1 j - 1); let v4 = getSum(BIT i - 1 j); // Assigning a value to a particular element // of 2D BIT updateBIT(BIT i j aux[i][j] - (v1 - v2 - v4 + v3)); } } return; } // A function to answer the queries function answerQueries(qmBIT) { for (let i = 0; i < m; i++) { let x1 = q[i].x1 + 1; let y1 = q[i].y1 + 1; let x2 = q[i].x2 + 1; let y2 = q[i].y2 + 1; let ans = getSum(BIT x2 y2) - getSum(BIT x2 y1 - 1) - getSum(BIT x1 - 1 y2) + getSum(BIT x1 - 1 y1 - 1); document.write('Query ('+q[i].x1+' ' +q[i].y1+' ' +q[i].x2+' ' +q[i].y2+') = ' +ans+'
'); } return; } // Driver Code let mat= [[1 2 3 4] [5 3 8 1] [4 6 7 5] [2 4 8 9]]; // Create a 2D Binary Indexed Tree let BIT = new Array(N + 1); for(let i=0;i<(N+1);i++) { BIT[i]=new Array(N+1); for(let j=0;j<(N+1);j++) { BIT[i][j]=0; } } construct2DBIT(mat BIT); /* Queries of the form - x1 y1 x2 y2 For example the query- {1 1 3 2} means the sub-matrix- y / 3 | 1 2 3 4 Sub-matrix 2 | 5 3 8 1 {1132} --. 3 8 1 1 | 4 6 7 5 6 7 5 0 | 2 4 8 9 | --|------ 0 1 2 3 ---. x | Hence sum of the sub-matrix = 3+8+1+6+7+5 = 30 */ let q = [new Query(1 1 3 2) new Query(2 3 3 3) new Query(1 1 1 1)]; let m = q.length; answerQueries(q m BIT); // This code is contributed by rag2127 </script>
Uitvoer
Query(1 1 3 2) = 30 Query(2 3 3 3) = 7 Query(1 1 1 1) = 6
Tijdcomplexiteit:
als anders in bash-shell
- Zowel de functie updateBIT(xy val) als de functie getSum(xy) nemen O(log(N)*log(M)) tijd in beslag.
- Voor het bouwen van de 2D BIT is O(NM log(N)*log(M)) nodig.
- Omdat we bij elk van de vragen de functie getSum(xy) aanroepen, is het beantwoorden van alle Q-vragen nodig O(Q*log(N)*log(M)) tijd.
- Vandaar de totale tijdscomplexiteit van het programma O((NM+Q)*log(N)*log(M)) waar
N = maximale X-coördinaat van de hele matrix.
M = maximale Y-coördinaat van de hele matrix.
Q = Aantal zoekopdrachten.
Hulpruimte: O(NM) om de BIT en de hulparray op te slaan
