De Tijdcomplexiteit van Samenvoegsortering is O(n logboek n) in zowel de gemiddeld En ergste gevallen . De ruimtecomplexiteit van Sorteer samen is Op) . 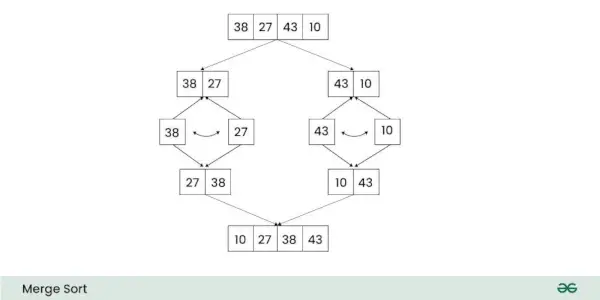
| Aspect | Complexiteit |
|---|---|
| Tijdcomplexiteit | O(n logboek n) |
| Ruimtecomplexiteit | Op) |
Tijdcomplexiteitsanalyse van samenvoegsortering:
Overweeg de volgende terminologieën:
T(k) = tijd die nodig is om k elementen te sorteren
M(k) = tijd die nodig is om k elementen samen te voegen
Er kan dus geschreven worden
T(N) = 2 * T(N/2) + M(N)
= 2 * T(N/2) + constante * N
Deze N/2-elementen zijn verder verdeeld in twee helften. Dus,
T(N) = 2 * [2 * T(N/4) + constante * N/2] + constante * N
= 4 * T(N/4) + 2 * N * constante
. . .
= 2k* T(N/2k) + k * N * constante
Het kan maximaal worden verdeeld totdat er één element over is. Dus dan N/2k= 1. k = logboek 2 N
T(N) = N * T(1) + N * logboek2N* constante
= N + N * logboek2N
Daarom is de tijdscomplexiteit O(N * logboek 2 N) .
Dus in het beste geval, het slechtste geval en het gemiddelde geval is de tijdscomplexiteit hetzelfde.
Ruimtecomplexiteitsanalyse van samenvoegsortering:
Sorteer samen heeft een complexiteit van de ruimte van Op) . Dit komt omdat het een extra array van grootte gebruikt N om de gesorteerde helften van de invoerarray samen te voegen. De hulparray wordt gebruikt om het samengevoegde resultaat op te slaan, en de invoerarray wordt overschreven met het gesorteerde resultaat.
