Er kunnen drie dimensies worden gemeten: lengte, breedte en hoogte, voor elk object dat u kunt zien of aanraken. Er zijn bepaalde afmetingen van ons huis waarin we leven. Het rechthoekige beeldscherm/monitor waar u naar kijkt heeft een breedte en breedte van de lengte. Van elke driedimensionale geometrische structuur worden oppervlakte en volume gemeten.
De ruimte die door het oppervlak van het object wordt bedekt, is de oppervlakte van een bepaald object. Terwijl de hoeveelheid beschikbare ruimte in een object volume is.
Inhoudsopgave
- Oppervlakte
- Totale oppervlakte
- Gebogen oppervlak/zijoppervlak
- Volume
- Voorbeelden van oppervlakten en volumes
- Veelgestelde vragen over oppervlakte- en volumeformules
Oppervlakte
Oppervlakte en volume kunnen voor elke driedimensionale (3D)geometrische vorm worden berekend. Het oppervlak van elk gebied is het gebied dat wordt ingenomen door het oppervlak van een object. Het volume is de hoeveelheid beschikbare ruimte in een object. We hebben verschillende soorten vormen, zoals een halve bol, bol, kubus, balk, cilinder, enz. Alle driedimensionale vormen hebben oppervlakte en volume. Maar tweedimensionale vormen zoals vierkanten, rechthoeken, driehoeken, cirkels, enz.
Hier in tweedimensionaal kunnen we alleen het gebied meten. Het gebied dat door het buitenoppervlak van een driedimensionaal object wordt ingenomen, wordt het oppervlak genoemd. Het wordt gemeten in vierkante eenheden.
Het gebied bestaat uit twee typen:
- Totale oppervlakte
- Gebogen oppervlak/zijoppervlak
Totale oppervlakte
De oppervlakte inclusief de basis(en) en het gebogen gedeelte komt overeen met de totale oppervlakte. Het is de hoeveelheid gebied die wordt omsloten door het oppervlak van het object. Als de vorm een gebogen basis en oppervlak heeft, zou de som van de twee gebieden de totale oppervlakte zijn. De totale oppervlakte kan worden gedefinieerd als de totale oppervlakte die door een object wordt bedekt, inclusief de basis en het gebogen deel. Als een object zowel een basis als een gebogen oppervlak heeft, is de totale oppervlakte gelijk aan de som van een basis en een gebogen oppervlak.
- De totale oppervlakte is de totale oppervlakte die door een object wordt ingenomen.
- Neem bijvoorbeeld een balk als voorbeeld. De balk heeft 6 vlakken, 12 randen en 8 hoekpunten.
Totale oppervlakte = basisoppervlak + gebogen oppervlak
postorder traversal van binaire boom
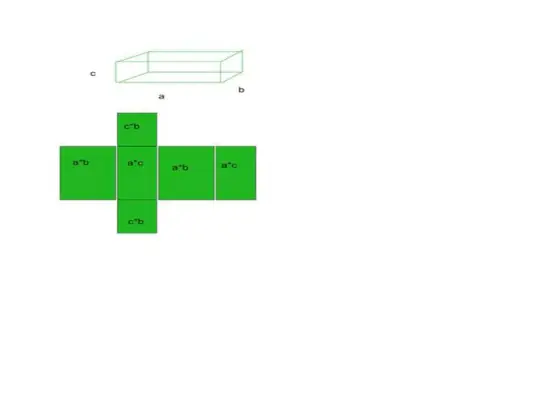
- De som van al die in totaal zes gebieden zal onze totale oppervlakte van de specifieke vorm zijn
Voorbeeld:
Hieronder is een balk weergegeven waarvan de afmeting is gegeven als lengte = 8 cm, breedte = 4 cm en hoogte = 6 cm, vind de TSA van een balk
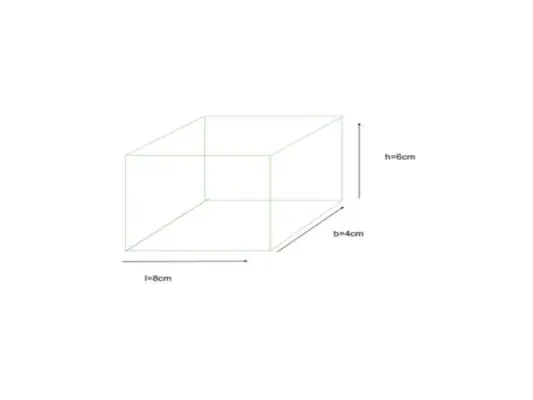
gegeven l = 8cm, b = 4cm, h = 6cm
TSA = 2((l * b) + (l * h) + (b * h))
= 2((8 * 4) + (8 * 6) + (4 * 6))
= 2((32) + (48) + (24))
= 2(104)
= 208
TSA van de balk is 208 cm.
Gebogen oppervlak/zijoppervlak
Het gebogen oppervlak, behalve het midden, komt overeen met de oppervlakte van alleen het gebogen gedeelte van de vorm(en). Voor vormen zoals een kegel wordt dit vaak het laterale oppervlak genoemd. Het laterale oppervlak kan worden gedefinieerd als het gebied dat alleen het gebogen oppervlak van een object of het laterale oppervlak van een object omvat door het basisgebied van een object uit te sluiten. Het laterale oppervlak wordt ook wel het gebogen oppervlak genoemd.
De meeste vormen of objecten verwijzen naar het gebogen oppervlak, de vorm of objectachtige cilinder verwijst ernaar als een lateraal oppervlak. Simpel gezegd: het gebied dat voor ons zichtbaar is, wordt een lateraal oppervlak genoemd. Beschouw bijvoorbeeld de cilinder zoals weergegeven in de onderstaande afbeelding.
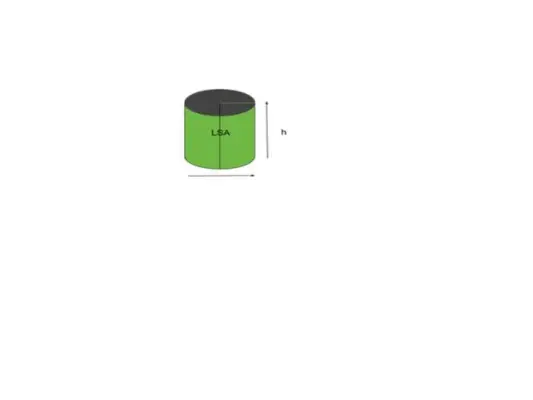
Volume
Volume is de hoeveelheid ruimte in een bepaald 3D-object. De totale hoeveelheid ruimte die een object of substantie inneemt, wordt volume genoemd. Het wordt gemeten in kubieke eenheden.
Formules van oppervlakte en volume
De gegeven tabel bevat het totale oppervlak, het gebogen oppervlak/zijoppervlak en het volume van verschillende vormen.
| Naam van vorm | Gebogen oppervlak | Totale oppervlakte | Volume |
|---|---|---|---|
| Kubusvormig | 2u(l + b) | 2(lb + bh + hl) | l * b * h |
| Kubus | 4a2 | 6a2 | A3 |
| Cilinder | 2π relatieve vochtigheid | 2π(r+h) | πr2H |
| Gebied | 4πr2 Java-keuzelijst | 4πr2 | 4/3πr3 |
| Kegel | πrl | πr(r + l) | 1/3πr2H |
| Halfrond | 2pr2 | 3πr2 | 2/3πr3 |
Lees verder:
- Oppervlakte van de piramide
- Oppervlakte van cilinder
- Oppervlakte van halfrond
- Oppervlakte van bol
- Oppervlakte van kubusvormig
Voorbeelden van oppervlakten en volumes
Voorbeeld 1: 2 kubussen elk met een inhoud van 512 cm 3 zijn van begin tot eind met elkaar verbonden. Vind de oppervlakte van de resulterende kubus?
Oplossing:
Gegeven,
Het volume (V) van elke kubus is = 512 cm3
we kunnen nu impliceren dat a3= 512 cm3
∴ Zijkant van de kubus, d.w.z. a = 8 cm
Nu zullen de breedte en lengte van de resulterende balk elk 8 cm zijn, terwijl de hoogte 16 cm zal zijn.
Dus de oppervlakte van de kubus (TSA) = 2(lb + bh + lh)
Door nu de waarden in te voeren, krijgen we:
= 2(8×16+8×8+16×8) cm 2
= (2×320) = 640 cm 2
Dus TSA van de balk = 640 cm 2
Voorbeeld 2: We hebben een cilindrische kaars met een diameter van 14 cm en een lengte van 2 cm. Het wordt gesmolten tot een kubusvormige kaars met de afmetingen 7 cm x 11 cm x 1 cm. Hoeveel kubusvormige kaarsen kunnen worden verkregen?
Oplossing:
Afmetingen van de cilindrische kaars:
Straal cilindervormige kaars = 14/2 cm = 7 cm
Hoogte/Dikte=2 cm
Volume van één cilindrische kaars = πr2h = π x 7 x 7 x (2) cm3= 308cm3.
Volume van kubusvormig kaars = 7 x 11 x 1 = 77 cm3
Dus aantal kubusvormige kaarsen = volume van kubusvormige kaars/volume van één cilindrische kaars = 308/77 = 4
Daarom kunnen we 4 kubusvormige kaarsen krijgen.
Voorbeeld 3: Een vrouw wil een bolvormige speelgoedbal van klei bouwen waarvan de straal gelijk is aan de straal van de armband die zij draagt. Omdat de armband rond van vorm is, wil ze ook dat de oppervlakte van de armband gelijk is aan het volume van de bol. Ontdek de straal van de armband die ze draagt?
Oplossing:
Laat r zowel de straal van de armband als de bol zijn,
Er is ons gegeven dat het volume van de bol gelijk is aan de oppervlakte van de armband:
Vandaar,
πr2= 4/3 πr3
⇒ r = 3/4
verschil inkorten en verwijderenDaarom is de straal van de armband 3/4 eenheden.
Voorbeeld 4: Er wordt aangenomen dat de schuine hoogte van een rechte, ronde kegel 25 cm is en de hoogte 24 cm. Vind het gebogen oppervlak van de kegel?
Oplossing:
De formule voor het gebogen oppervlak van de kegel is πrl. Waar r de straal van de kegel is en l de schuine hoogte van de kegel.
Hier is de kegel de rechter ronde kegel.
De straal van de kegel zou dus zijn:
r= sqrt{l^2 – h^2}
=>r = sqrt{25^2 – 24^2}
=> r = 7 cm.
Het berekenen van het gebogen oppervlak is nu:
Benodigde oppervlakte = (22/7) * 7 * 25 = 550 cm2
Het gebogen oppervlak van de kegel is dus 550 cm2 2 .
Voorbeeld 5: Zoek het zijoppervlak van een cilinder met een basisradius van 6 inch en een hoogte van 14 inch.
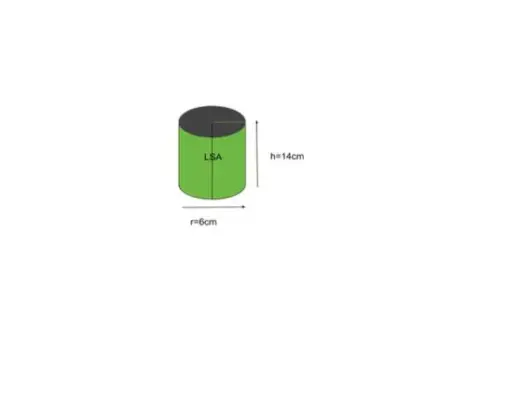
Oplossing:
Gegeven straal r = 6, hoogte h = 14
LSA = 2∏rh
= 2 * ∏ * 6 * 14
= 168∏
= 527.787
= 528.
De LSA van een bepaalde cilinder is 528 cm .
Oefenvraag over oppervlakten en volumes
Verscheidene Oefenvragen over oppervlakten en volume formules zijn:
Q1. Bereken de oppervlakte van een kubus met een zijdelengte van 5 centimeter.
Vraag 2. Bereken het volume van een bol met een straal van 3 meter.
Q3. Bepaal de totale oppervlakte van een cilinder met een straal van 4 centimeter en een hoogte van 8 centimeter.
Q4. Zoek het volume van een kegel met een straal van 6 inch en een hoogte van 10 inch.
Vraag 5. Bereken de oppervlakte van een rechthoekig prisma met een lengte van 7 meter, een breedte van 4 meter en een hoogte van 6 meter.
Veelgestelde vragen over oppervlakte- en volumeformules
Wat zijn de formules voor oppervlakte en volume?
In bovenstaand artikel zijn diverse oppervlakte- en volumeformules toegevoegd.
Wat is de formule voor oppervlaktevolume Klasse 10?
Formule voor oppervlakte- en volumeklasse 10 bevat:
| Naam van vorm | Gebogen oppervlak | Totale oppervlakte | Volume |
|---|---|---|---|
| Kubusvormig primaire sleutel en samengestelde sleutel in sql | 2 uur(l + b) | 2(lb + bh + hl) | l × b × h |
| Kubus | 4a2 | 6a2 | A3 |
| Cilinder | 2π relatieve vochtigheid | 2π(r+h) | πr2H |
| Gebied | 4πr2 | 4πr2 | 4/3πr3 |
| Kegel | πrl | πr(r + l) | 1/3πr2H |
| Halfrond | 2pr2 | 3πr2 | 2/3πr3 |
Wat is de formule van Cuboid in oppervlakte en volume?
- Oppervlakte van kubusvormig = 2 (lb + bh + hl)
- Volume van Cubiod = l × b × h
Wat is oppervlakte en volume?
Oppervlakte is de oppervlakte van alle oppervlakken van een vaste stof en het volume ervan is de ruimte die wordt ingenomen door de sloid.
