De standaardvorm van een parabool is y = ax2+ bx + c waarbij a, b en c reële getallen zijn en a niet gelijk is aan nul. Een parabool wordt gedefinieerd als de verzameling van alle punten in een vlak die op gelijke afstand liggen van een vaste lijn en een vast punt in het vlak.
In dit artikel zullen we in detail begrijpen wat een parabool is, de standaardvergelijking van een parabool, gerelateerde voorbeelden en andere.
Inhoudsopgave
- Wat is een parabool?
- Vergelijking van een parabool
- Delen van een parabool
- Voorbeelden van vergelijking van een parabool
Wat is een parabool?
Een parabool is een kegelsnede die wordt gedefinieerd als de verzameling van alle punten die op gelijke afstand liggen van een punt dat het brandpunt wordt genoemd en een lijn die de richtlijn wordt genoemd. De standaardvergelijkingen voor een parabool zijn afhankelijk van de oriëntatie (openingsrichting) en positie.
Vergelijking van een parabool
De vergelijking van een parabool kan in standaardvorm of algemene vorm worden geschreven en beide worden hieronder toegevoegd:
Algemene vergelijkingen van een parabool
De algemene vergelijking van een parabool is:
y = 4a(x – h) 2 + k
(of)
x = 4a(y – k) 2 + h
Waar (h, k) het hoekpunt van een parabool is.
Standaardvergelijkingen van een parabool
De standaardvergelijking van een parabool is:
y = bijl 2 + bx + c
(of)
x = is 2 + door + c
waarbij a nooit nul kan zijn.
Delen van een parabool
Enkele belangrijke termen en onderdelen van een parabool zijn:
- Focus: Focus is het vaste punt van een parabool.
- Richtlijn: De richtlijn van een parabool is de lijn loodrecht op de as van een parabool.
- Brandpuntsakkoord: Het akkoord dat door het brandpunt van een parabool gaat en de parabool op twee verschillende punten doorsnijdt, wordt het brandpuntakkoord genoemd.
- Brandpuntsafstand: De brandpuntsafstand is de afstand van een punt (x1, En1) op de parabool vanuit het brandpunt.
- Rechter zijde: Een latus rectum is een brandpuntskoord dat door het brandpunt van een parabool loopt en loodrecht op de as van de parabool staat. De lengte van het latus rectum is LL’ = 4a.
- Excentriciteit: De verhouding tussen de afstand van een punt tot het brandpunt en de afstand tot de richtlijn wordt excentriciteit (e) genoemd. Voor een parabool is de excentriciteit gelijk aan 1, d.w.z. e = 1.
Een parabool heeft vier standaardvergelijkingen gebaseerd op de oriëntatie van de parabool en zijn as. Elke parabool heeft een andere dwarsas en geconjugeerde as.
| Vergelijking van parabool | Parabool | Formules van parameters van een parabool |
|---|---|---|
| En 2 = 4ax | 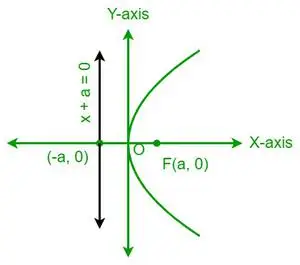 Horizontale parabool |
|
| En 2 = -4ax |  Horizontale parabool |
|
| X 2 = 4ay |  Verticale parabool |
|
| X 2 = -4ay |  Verticale parabool |
|
Hieronder volgen de waarnemingen die zijn gedaan op basis van de standaardvorm van vergelijkingen van een parabool:
- Een parabool is symmetrisch ten opzichte van zijn as. Bijvoorbeeld, y2= 4ax is symmetrisch ten opzichte van de x-as, terwijl x2= 4ay is symmetrisch ten opzichte van de y-as.
- Als een parabool symmetrisch is rond de x-as, dan opent de parabool naar rechts als de x-coëfficiënt positief is en naar links als de x-coëfficiënt negatief is.
- Als een parabool symmetrisch is rond de y-as, dan opent de parabool naar boven als de y-coëfficiënt positief is en naar beneden als de y-coëfficiënt negatief is.
Hieronder volgen de standaardvergelijkingen van een parabool wanneer de symmetrieas evenwijdig is aan de x-as of de y-as en het hoekpunt zich niet in de oorsprong bevindt.
| Vergelijking van parabool | Parabool | Formules van parameters van een parabool |
|---|---|---|
| (en – k)2= 4a(x – h) |  Horizontale parabool |
|
| (en – k)2= -4a(x – h) |  Horizontale parabool |
|
| (x – h)2= 4a(y – k) |  Verticale parabool |
|
| (x – h)2= -4a(y – k) |  Verticale parabool |
|
Vergelijking van paraboolafleiding
Laat P een punt op de parabool zijn waarvan de coördinaten (x, y) zijn. Volgens de definitie van een parabool is de afstand van punt P tot het brandpunt (F) gelijk aan de afstand van hetzelfde punt P tot de richtlijn van een parabool. Laten we nu een punt X op de richtlijn bekijken, waarvan de coördinaten (-a, y) zijn.
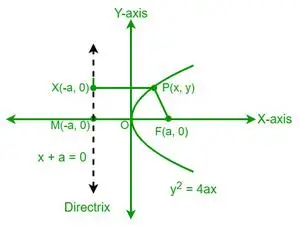
Van de definitie van de excentriciteit van een parabool hebben we
e = PF/PX = 1
⇒ PF = PX
De coördinaten van de focus zijn (a, 0). Door nu de coördinatenafstandsformule te gebruiken, kunnen we de afstand van punt P (x, y) tot het brandpunt F (a, 0) vinden.
PF = √[(x – a)2+ (en – 0)2]
⇒ PF = √[(x – a)2+ en2] ------ (1)
De vergelijking van de richtlijn is x + a = 0. Om de afstand van PX te vinden, gebruiken we de loodrechte afstandsformule.
PX = (x + a)/√[12+02]
⇒ PX = x +a —————— (2)
We weten al dat PF = PX. Stel vergelijkingen (1) en (2) dus gelijk.
√[(x – a)2+ en2] = (x + een)
Door aan beide kanten het kwadraat te maken, krijgen we:
⇒ [(x – a)2+ en2] = (x + een)2
⇒x2+ een2– 2ax + y2= x2+ een2+ 2ax
⇒ en2– 2ax = 2ax
⇒ en2= 2ax + 2ax ⇒ En 2 = 4ax
We hebben dus de vergelijking van een parabool afgeleid. Op dezelfde manier kunnen we de standaardvergelijkingen van de andere drie parabolen afleiden.
- En2= -4ax
- X2= 4ay
- X2= -4ay
En 2 = 4ax, en 2 = -4ax, x 2 = 4ay, en x 2 = -4ay zijn de standaardvergelijkingen van een parabool.
Artikelen gerelateerd aan Parabool:
- Vergelijking van cirkel
- Vergelijking van ellips
- Vergelijking van hyperbool
- Toepassingen van parabool in het echte leven
Voorbeelden van vergelijking van een parabool
Voorbeeld 1: Zoek de lengte van het latus rectum, het brandpunt en het hoekpunt, als de vergelijking van de parabool y is 2 = 12x.
Oplossing:
Gegeven,
Vergelijking van de parabool is y2= 12x
Door de gegeven vergelijking te vergelijken met de standaardvorm y2= 4ax
4a = 12
⇒ a = 12/4 = 3
We weten dat,
Rechterzijde van een parabool = 4a = 4 (3) = 12
Nu, focus van de parabool = (a, 0) = (3, 0)
Hoekpunt van de gegeven parabool = (0, 0)
Voorbeeld 2: Zoek de vergelijking van de parabool die symmetrisch is rond de X-as en door het punt (-4, 5) gaat.
Oplossing:
Gegeven,
Parabool is symmetrisch rond de X-as en heeft zijn hoekpunt in de oorsprong.
De vergelijking kan dus de vorm y hebben2= 4ax of y2= -4ax, waarbij het teken afhangt van het feit of de parabool naar links of naar rechts opent.
De parabool moet naar links openen omdat hij door (-4, 5) gaat, dat in het tweede kwadrant ligt.
De vergelijking wordt dus: y2= -4ax
Vervanging van (-4, 5) in de bovenstaande vergelijking,
⇒ (5)2= -4a(-4)
⇒ 25 = 16a
⇒ a = 25/16
Daarom is de vergelijking van de parabool: y2= -4(25/16)x (of) 4y2= -25x.
Voorbeeld 3: Zoek de coördinaten van het brandpunt, de as, de vergelijking van de richtlijn en de latus rectum van de parabool x 2 = 16j.
Oplossing:
Gegeven,
Vergelijking van de parabool is: x2= 16j
Door de gegeven vergelijking te vergelijken met de standaardvorm x2= 4ay,
4a = 16 ⇒ een = 4
De coëfficiënt van y is positief, dus de parabool opent naar boven.
Ook ligt de symmetrieas langs de positieve Y-as.
Vandaar,
Het brandpunt van de parabool is (a, 0) = (4, 0).
Vergelijking van de richtlijn is y = -a, d.w.z. y = -4 of y + 4 = 0.
Lengte van het latus rectum = 4a = 4(4) = 16.
Voorbeeld 4: Vind de lengte van het latus rectum, het brandpunt en het hoekpunt als de vergelijking van een parabool 2(x-2) is 2 + 16 = j.
Oplossing:
Gegeven,
Vergelijking van een parabool is 2(x-2)2+ 16 = en
Door de gegeven vergelijking te vergelijken met de algemene vergelijking van een parabool y = a(x – h)2+ k, we krijgen
een = 2
(h, k) = (2, 16)
We weten dat,
Lengte van latus rectum van een parabool = 4a
= 4(2) = 8
Nu, focus= (a, 0) = (2, 0)
Nu, hoekpunt = (2, 16)
Voorbeeld 5: Vergelijking van een parabool is x 2 – 12x + 4y – 24 = 0, zoek dan het hoekpunt, de focus en de richtlijn.
Oplossing:
Gegeven,
Vergelijking van de parabool is x2– 12x + 4j – 24 = 0
⇒x2– 12x + 36 – 36 + 4y – 24 = 0
⇒ (x – 6)2+ 4j – 60 = 0
⇒ (x – 6)2= -4(j + 15)
De verkregen vergelijking heeft de vorm van (x – h)2= -4a(y – k)
-4a = -4 ⇒ a = 1
Dus het hoekpunt = (h, k) = (6, – 15)
Focus = (h, k – a) = (6, -15-1) = (6, -16)
Vergelijking van de richtlijn is y = k + a
⇒ y = -15 + 1 ⇒ y = -14
⇒ j + 14 = 0
Veelgestelde vragen over vergelijking van parabool
Hoe vind je de standaardvergelijking van een parabool?
De standaardvorm van een parabool is y2= 4ax of x2= 4ay.
Wat is de normale vergelijking van parabool?
Vergelijking van normaal met de parabool y2= 4ax met een helling m wordt gegeven als: y = mx – 2 uur – uur 3
Hoe vind je het hoekpunt van een parabool?
Voor gegeven parabool: y = ax2+ bx + c het hoekpunt ervan kan worden gevonden met behulp van de formule x = − b/2a. Voer deze x-waarde terug in de vergelijking om de overeenkomstige y-coördinaat te vinden.
CSS-teruglooptekst
