Sin Cos-formules in trigonometrie: Trigonometrie is, zoals de naam al aangeeft, de studie van driehoeken. Het is een belangrijke tak van de wiskunde die de relatie tussen de lengtes van de zijden en de hoeken van de rechthoekige driehoek bestudeert en ook helpt bij het bepalen van de ontbrekende lengtes of hoeken van een driehoek. Er zijn zes trigonometrische verhoudingen of functies: sinus, cosinus, tangens, cosecans, secans en cotangens, waarbij cosecans, secans en cotangens de wederzijdse functies zijn van de andere drie functies, dat wil zeggen respectievelijk sinus, cosinus en tangens.
Een trigonometrische verhouding wordt gedefinieerd als de verhouding van de zijdelengten van een rechthoekige driehoek. Trigonometrie wordt op verschillende gebieden in ons dagelijks leven gebruikt. Het helpt bij het bepalen van de hoogte van heuvels of gebouwen. Het wordt ook gebruikt op gebieden als criminologie, constructie, natuurkunde, archeologie, scheepsmotortechniek, enz.
In dit artikel zullen we ze allemaal verkennen trigonometrieformules, voornamelijk sin- en cos-formules met hun voorbeelden, en een lijst met alle formules in trigonometrie.
Inhoudsopgave
- Formules in trigonometrie
- Enkele basisformules voor Sin Cos
- Sin Cos-formuletabel
- Voorbeelden van Sin Cos-formules
- Oefenproblemen met Sin Cos-formules in trigonometrie met voorbeelden
Formules in trigonometrie
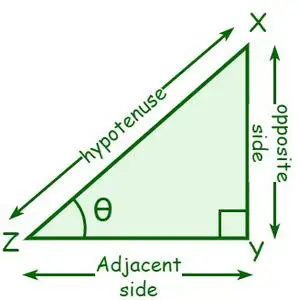
Laten we een rechthoekige driehoek XYZ bekijken, waarbij ∠Y = 90°. Laat de hoek bij hoekpunt Z θ zijn. De zijde grenzend aan θ wordt de aangrenzende zijde genoemd, en de zijde tegenover θ wordt de tegenoverliggende zijde genoemd. Een hypotenusa is een zijde tegenovergesteld aan de rechte hoek of de langste zijde van een rechte hoek.
- sin θ = tegenoverliggende zijde/hypotenusa
- cos θ = aangrenzende zijde/hypotenusa
- tan θ = tegenoverliggende zijde/aangrenzende zijde
- cosec θ = 1/sin θ = Hypotenusa/tegengestelde kant
- sec θ = 1/ cos θ = hypotenusa/aangrenzende zijde
- kinderbed θ = 1/ bruin θ = aangrenzende zijde/tegenoverliggende zijde
Sinus-formule
De sinus van een hoek in een rechthoekige driehoek is de verhouding tussen de lengte van de tegenoverliggende zijde en de lengte van de hypotenusa tot de gegeven hoek. Een sinusfunctie wordt weergegeven als sin.
sin θ = tegenoverliggende zijde/hypotenusa
Cosinus formule
De cosinus van een hoek in een rechthoekige driehoek is de verhouding tussen de lengte van de aangrenzende zijde en de lengte van de hypotenusa tot de gegeven hoek. Een cosinusfunctie wordt weergegeven als cos.
hoe je een map Linux kunt hernoemencos θ = aangrenzende zijde/hypotenusa
Enkele basisformules voor Sin Cos
Sinus- en cosinusfuncties in kwadranten
- De sinusfunctie is positief in het eerste en tweede kwadrant en negatief in het derde en vierde kwadrant.
- De cosinusfunctie is positief in het eerste en vierde kwadrant en negatief in het tweede en derde kwadrant.
Graden
Kwadrant
Teken van sinusfunctie
Teken van cosinusfunctie
0° tot 90°
1e kwadrant
+ (positief)
+ (positief)
90° tot 180°
2e kwadrant
+ (positief)
– (negatief)
180° tot 270°
3e kwadrant
– (negatief)
– (negatief)
270° tot 360°
4e kwadrant
– (negatief)
+ (positief)
De negatieve hoekidentiteit van de sinus- en cosinusfuncties
- De sinus van een negatieve hoek is altijd gelijk aan de negatieve sinus van de hoek.
zonde (– θ) = – zonde θ
- De cosinus van een negatieve hoek is altijd gelijk aan de cosinus van de hoek.
cos (– θ) = cos θ
Relatie tussen sinus- en cosinusfunctie
sin θ = cos (90° – θ)
Reciproque functies van de sinus- en cosinusfuncties
- Een Cosecant-functie is de reciproque functie van de sinusfunctie.
cosec θ = 1/sin θ
- Een secansfunctie is de reciproque functie van de cosinusfunctie.
sec θ = 1/cos θ
Pythagoras identiteit
zonder 2 θ + cos 2 θ = 1
Periodieke identiteiten van de sinus- en cosinusfuncties
zonde (θ + 2nπ) = zonde θ
cos (θ + 2nπ) = cos θ
Dubbele hoekformules voor de sinus- en cosinusfuncties
zonde 2θ = 2 zonde θ cos θ
cos 2θ = cos 2 θ – zonde 2 θ = 2 cos 2 θ – 1 = 1 – 2 zonde 2 i
Halve hoekidentiteiten voor de sinus- en cosinusfuncties
sin (θ/2) = ±√[(1 – cos θ)/2]
cos (θ/2) = ±√[(1 + cos θ)/2]
Drievoudige hoekidentiteiten voor de sinus- en cosinusfuncties
zonde 3θ = 3 zonde θ – 4 zonde 3 i
cos 3θ = 4cos 3 θ – 3 cos θ
Som- en verschilformules
- Sinus-functie
zonde (A + B) = zonde A cos B + cos A zonde B
zonde (A – B) = zonde A cos B – cos A zonde B
- Cosinus-functie
cos (A + B) = cos A cos B – zonde A zonde B
cos (A – B) = cos A cos B + sin A zonde B
Wet van sinussen of sinusregel
De wet van de sinusregel is een trigonometrische wet die een verband geeft tussen de lengtes van de zijden en de hoeken van een driehoek.

a/zonde A = b/zonde B = c/zonde C
Waar a, b en c de lengtes zijn van de drie zijden van de driehoek ABC, en A, B en C de hoeken zijn.
Wet van cosinus
De cosinusregel van de cosinusregel wordt gebruikt om de ontbrekende of onbekende hoeken of zijdelengtes van een driehoek te bepalen.

A 2 = geb 2 + c 2 – 2bc cos A
B 2 = c 2 + een 2 – 2ca cos B
C 2 = een 2 + b 2 – 2ab cos C
Waar a, b en c de lengtes zijn van de drie zijden van de driehoek ABC, en A, B en C de hoeken zijn.
Sin Cos-formuletabel
Hier is de tabel/lijst met Sin- en Cos-formules voor verschillende hoeken in graden en radialen:
Sin Cos-formulelijst
| Hoek (in graden) | Hoek (in radialen) | zonde ik | cos θ |
|---|---|---|---|
| 0° | 0 | 0 | 1 |
| 30° | p/6 | 1/2 | _3/2 |
| 45° | p/4 | 1/√2 | 1/√2 |
| 60° | p/3 | √3/2 | 1/2 |
| 90° | p/2 | 1 | 0 |
| 120° | 2p/3 | √3/2 | -1/2 |
| 150° | 5p/6 | 1/2 | -√3/2 |
| 180° sorteer een arraylist in Java | Pi | 0 | -1 |
Voorbeelden van Sin Cos-formules
Probleem 1: Als cos α = 24/25, zoek dan de waarde van sin α.
Oplossing:
Gegeven,
cos α = 24/25
Van de identiteiten van Pythagoras die we hebben;
want2θ + zonde2θ = 1
(24/25)2+ zonder2α = 1
zonder2α = 1 – (24/25)2
zonder2α = 1 – (576/625) = (625 – 576)/625
zonder2α = (625 – 576)/625 = 49/626
zonde α = √49/625 = ±7/25
Daarom sin α = ±7/25.
Probleem 2: Bewijs de formules sin 2A en cos 2A, als ∠A= 30°.
Oplossing:
Gegeven, ∠A= 30°
We weten dat,
1) zonde 2A = 2 zonde A cos A
sin 2(30°) = 2 sin 30° cos 30°
sin 60° = 2 × (1/2) × (√3/2) {Aangezien sin 30° = 1/2, cos 30° = √3/2 en sin 60° = √3/2}
√3/2 = √3/2
LHS = RHS
2) cos 2A = 2cos2EEN – 1
cos 2(30°) = 2cos2(30°) – 1
cos 60° = 2(√3/2)2– 1 = 3/2 – 1 {Aangezien cos 60° = 1/2 en cos 30° = √3/2}
1/2 = 1/2
LHS = RHS
Bewezen dus.
Probleem 3: Vind de waarde van cos x, als tan x = 3/4.
Oplossing:
Gegeven, bruin x = 3/4
We weten dat,
bruin x = tegenoverliggende zijde/aangrenzende zijde = 3/4
Om de hypotenusa te vinden, gebruiken we de stelling van Pythagoras:
hypotenusa2= tegenovergesteld2+ aangrenzend2
H2= 32+ 42
H2= 9 + 16 = 25
H = √25 = 5
Nu, cos x = aangrenzende zijde/hypotenusa
cos x = 4/5
De waarde van cos x is dus 4/5.
Probleem 4: Vind ∠C (in graden) en ∠A (in graden), als ∠B = 45°, BC = 15 inch en AC = 12 inch.

Oplossing:
Gegeven: ∠B = 45°, BC = a = 15 inch, en AC = b = 12 inch.
Van de wet van de sinussen hebben we dat gedaan
a/zonde A = b/zonde B = c/zonde C
⇒ a/zonde A = b/zonde B
⇒ 15/sin A = 12/sin 45°
⇒ 15/sin A = 12/(1/√2)
⇒ 15/sin A = 12√2 = 16,97
⇒ zonder A = 15/16,97 = 0,8839
⇒ ∠A = zonde-1(0,8839) = 62,11°
We weten dat de som van de binnenhoeken van een driehoek 180° is.
Dus ∠A + ∠B + ∠C = 180°
⇒ 62,11° + 45° + ∠C = 180°
⇒ ∠C = 180° – (62,11° + 45°) = 72,89°
Daarom is ∠A = 62,11° en ∠C = 72,89°.
Probleem 5: Bewijs de halve-hoekidentiteiten van de cosinusfunctie.
Oplossing:
De halve-hoekidentiteit van de cosinusfunctie is:
cos (θ/2) = ±√[(1 + cos θ)/2]
Vanuit dubbele hoekidentiteiten hebben we:
cos 2A = 2 cos2EEN – 1
Vervang nu A door θ/2 aan beide zijden
⇒ cos 2(θ/2) = 2 cos2(i/2) – 1
⇒ cos θ = 2 cos2(i/2) – 1
⇒ 2cos2(θ/2) = cosθ + 1
⇒ cos2(θ/2) = (cos θ + 1)/2
⇒ cos (θ/2) = ±√[(1 + cos θ)/2]
Bewezen dus.
Oefenproblemen met Sin Cos-formules in trigonometrie met voorbeelden
1. Gegeven sin θ = 3/5. Zoek cos θ.
2. Bewijs de identiteit sin(2A) = 2 sinA cosA voor A=45∘.
3. Als cos α = 5/13. Zoek zonde(2a).
4. Los θ op als sin θ = cos(90∘−θ).
5. Als tan β = 2. Vind sin β en cos β met behulp van de identiteit van Pythagoras.
Veelgestelde vragen over Sin Cos-formules in trigonometrie met voorbeelden
Wat zijn de fundamentele sinus- en cosinusformules in trigonometrie?
De basisformules voor sinus en cosinus zijn sin θ = tegenover/hypotenusa en cos θ = aangrenzend/hypotenusa, waarbij θ een hoek is in een rechthoekige driehoek.
Hoe vind je de sinus en cosinus van speciale hoeken?
Speciale hoeken zoals 0∘, 30∘, 45∘, 60∘ en 90∘ hebben specifieke sinus- en cosinuswaarden die kunnen worden onthouden met behulp van trigonometrische tabellen of eenheidscirkelconcepten.
Wat is de relatie tussen sinus- en cosinusfuncties?
De sinus- en cosinusfuncties zijn gerelateerd door de identiteit zonde θ = cos(90∘- θ) en de identiteit van Pythagoras zonder 2 θ+cos 2 θ = 1.
Hoe gebruik je de dubbele hoekformules voor sinus en cosinus?
De formules voor dubbele hoeken zijn zonde(2θ) = 2sinθcosθ En cos(2θ)=cos 2 θ – zonde 2 i. Deze worden gebruikt om trigonometrische functies van dubbele hoeken uit te drukken in termen van enkele hoeken.
Hoe vind je de waarden van sinus en cosinus voor hoeken in verschillende kwadranten?
De tekens van sinus- en cosinusfuncties zijn afhankelijk van het kwadrant waarin de hoek ligt:
- Eerste kwadrant: sin θ> 0 en cos θ> 0
- Tweede kwadrant: sin θ> 0 en cos θ <0
- Derde kwadrant: sinθ <0 en cosθ < 0
- Vierde kwadrant: sinθ 0
