Voorwaarde: Lineaire regressie
Lineaire regressie is een machine learning-algoritme gebaseerd op begeleid leren. Het voert een regressietaak uit. Regressie modelleert een doelvoorspellingswaarde op basis van onafhankelijke variabelen. Het wordt meestal gebruikt om de relatie tussen variabelen en prognoses te achterhalen. Verschillende regressiemodellen verschillen op basis van: het soort relatie tussen de afhankelijke en onafhankelijke variabelen waarmee ze rekening houden en het aantal onafhankelijke variabelen dat wordt gebruikt. In dit artikel wordt gedemonstreerd hoe u de verschillende Python-bibliotheken kunt gebruiken om lineaire regressie op een bepaalde gegevensset te implementeren. We zullen een binair lineair model demonstreren omdat dit gemakkelijker te visualiseren is. In deze demonstratie gebruikt het model Gradient Descent om te leren. Je kunt er hier meer over leren.
Stap 1: Importeren van alle benodigde bibliotheken
Python3
import> numpy as np> import> pandas as pd> import> seaborn as sns> import> matplotlib.pyplot as plt> from> sklearn>import> preprocessing, svm> from> sklearn.model_selection>import> train_test_split> from> sklearn.linear_model>import> LinearRegression> |
>
>
Stap 2: De dataset lezen:
Python3
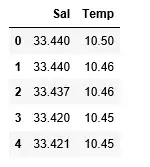
df>=> pd.read_csv(>'bottle.csv'>)> df_binary>=> df[[>'Salnty'>,>'T_degC'>]]> > # Taking only the selected two attributes from the dataset> df_binary.columns>=> [>'Sal'>,>'Temp'>]> #display the first 5 rows> df_binary.head()> |
computerwerk
>
>
Uitgang:
Stap 3: Onderzoek naar de gegevensspreiding
Python3
#plotting the Scatter plot to check relationship between Sal and Temp> sns.lmplot(x>=>'Sal'>, y>=>'Temp'>, data>=> df_binary, order>=> 2>, ci>=> None>)> plt.show()> |
>
>
Uitgang:

Stap 4: Gegevens opschonen
Python3
# Eliminating NaN or missing input numbers> df_binary.fillna(method>=>'ffill'>, inplace>=> True>)> |
>
>
Stap 5: Ons model trainen
Indiase actrice Rani Mukerji
Python3
X>=> np.array(df_binary[>'Sal'>]).reshape(>->1>,>1>)> y>=> np.array(df_binary[>'Temp'>]).reshape(>->1>,>1>)> > # Separating the data into independent and dependent variables> # Converting each dataframe into a numpy array> # since each dataframe contains only one column> df_binary.dropna(inplace>=> True>)> > # Dropping any rows with Nan values> X_train, X_test, y_train, y_test>=> train_test_split(X, y, test_size>=> 0.25>)> > # Splitting the data into training and testing data> regr>=> LinearRegression()> > regr.fit(X_train, y_train)> print>(regr.score(X_test, y_test))> |
rij en kolom
>
>
Uitgang:

Stap 6: Onze resultaten verkennen
Python3
y_pred>=> regr.predict(X_test)> plt.scatter(X_test, y_test, color>=>'b'>)> plt.plot(X_test, y_pred, color>=>'k'>)> > plt.show()> # Data scatter of predicted values> |
>
>
Uitgang:

De lage nauwkeurigheidsscore van ons model suggereert dat ons regressieve model niet erg goed aansluit bij de bestaande gegevens. Dit suggereert dat onze gegevens niet geschikt zijn voor lineaire regressie. Maar soms kan een dataset een lineaire regressor accepteren als we slechts een deel ervan beschouwen. Laten we die mogelijkheid eens onderzoeken.
Stap 7: Werken met een kleinere dataset
java-arraylijst
Python3
df_binary500>=> df_binary[:][:>500>]> > # Selecting the 1st 500 rows of the data> sns.lmplot(x>=>'Sal'>, y>=>'Temp'>, data>=> df_binary500,> >order>=> 2>, ci>=> None>)> |
>
>
Uitgang:

We kunnen al zien dat de eerste 500 rijen een lineair model volgen. Ga verder met dezelfde stappen als voorheen.
Python3
df_binary500.fillna(method>=>'fill'>, inplace>=> True>)> > X>=> np.array(df_binary500[>'Sal'>]).reshape(>->1>,>1>)> y>=> np.array(df_binary500[>'Temp'>]).reshape(>->1>,>1>)> > df_binary500.dropna(inplace>=> True>)> X_train, X_test, y_train, y_test>=> train_test_split(X, y, test_size>=> 0.25>)> > regr>=> LinearRegression()> regr.fit(X_train, y_train)> print>(regr.score(X_test, y_test))> |
>
>
Uitgang:

Python3
y_pred>=> regr.predict(X_test)> plt.scatter(X_test, y_test, color>=>'b'>)> plt.plot(X_test, y_pred, color>=>'k'>)> > plt.show()> |
>
>
python afdrukken tot 2 decimalen
Uitgang:

Stap 8: Evaluatiestatistieken voor regressie
Ten slotte controleren we de prestaties van het lineaire regressiemodel met behulp van evaluatiestatistieken. Voor regressie-algoritmen gebruiken we op grote schaal de metrieken mean_absolute_error en mean_squared_error om de prestaties van het model te controleren.
Python3
from> sklearn.metrics>import> mean_absolute_error,mean_squared_error> > mae>=> mean_absolute_error(y_true>=>y_test,y_pred>=>y_pred)> #squared True returns MSE value, False returns RMSE value.> mse>=> mean_squared_error(y_true>=>y_test,y_pred>=>y_pred)>#default=True> rmse>=> mean_squared_error(y_true>=>y_test,y_pred>=>y_pred,squared>=>False>)> > print>(>'MAE:'>,mae)> print>(>'MSE:'>,mse)> print>(>'RMSE:'>,rmse)> |
>
>
Uitgang:
MAE: 0.7927322046360309 MSE: 1.0251137190180517 RMSE: 1.0124789968281078>
