Gegeven een array arr[] wat een vertegenwoordigt Volledige binaire boom d.w.z. als index ik is de ouder index 2*ik + 1 is de linker kind En index 2*i+2 is het juiste kind. De taak is om de minimum aantal van ruilt nodig om het om te zetten in een Binaire zoekboom.
Voorbeelden:
Invoer: arr[] = [5 6 7 8 9 10 11]
Uitgang: 3
Uitleg:
Binaire boom van de gegeven array:

Wissel 1: Verwissel knooppunt 8 met knooppunt 5.
Wissel 2: Verwissel knooppunt 9 met knooppunt 10.
Wissel 3: Verwissel knooppunt 10 met knooppunt 7.Er zijn dus minimaal 3 swaps vereist om de onderstaande binaire zoekboom te verkrijgen:
beste glimlach ter wereld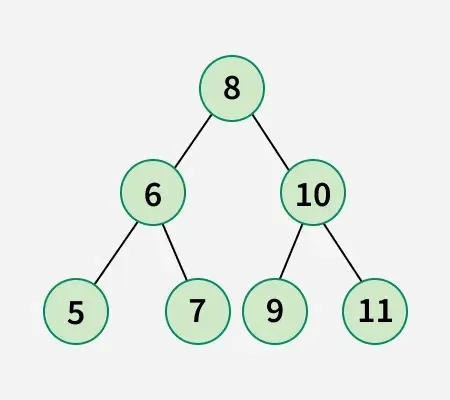
Invoer: arr[] = [1 2 3]
Uitgang: 1
Uitleg:
Binaire boom van de gegeven array: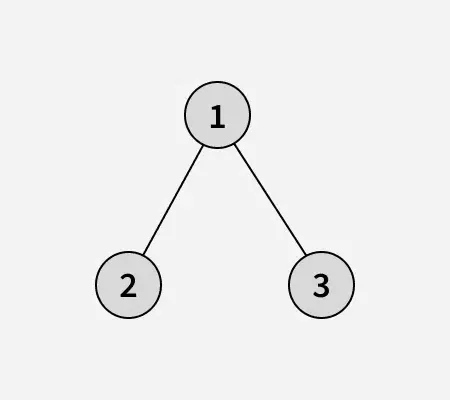
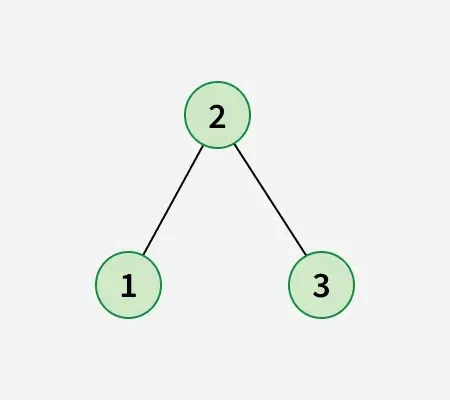
Na het verwisselen van knooppunt 1 met knooppunt 2 verkrijgt u de onderstaande binaire zoekboom:
Benadering:
C++Het idee is om het feit dat te gebruiken ongeordende doortocht van Binaire zoekboom is binnen toenemend volgorde van hun waarde.
Dus zoek de ongeordende doortocht van de binaire boom en sla het op in de array en probeer het soort de array. De minimaal aantal swaps dat nodig is om de array te sorteren zal het antwoord zijn.
// C++ program for Minimum swap required // to convert binary tree to binary search tree #include
// Java program for Minimum swap required // to convert binary tree to binary search tree import java.util.Arrays; class GfG { // Function to perform inorder traversal of the binary tree // and store it in an array static void inorder(int[] arr int[] inorderArr int index int[] counter) { int n = arr.length; // Base case: if index is out of bounds return if (index >= n) return; // Recursively visit left subtree inorder(arr inorderArr 2 * index + 1 counter); // Store current node value in the inorder array inorderArr[counter[0]] = arr[index]; counter[0]++; // Recursively visit right subtree inorder(arr inorderArr 2 * index + 2 counter); } // Function to calculate minimum swaps // to sort inorder traversal static int minSwaps(int[] arr) { int n = arr.length; int[] inorderArr = new int[n]; int[] counter = new int[1]; // Get the inorder traversal of the binary tree inorder(arr inorderArr 0 counter); // Create an array of pairs to store the value // and its original index int[][] t = new int[n][2]; int ans = 0; // Store the value and its original index for (int i = 0; i < n; i++) { t[i][0] = inorderArr[i]; t[i][1] = i; } // Sort the array based on values to get BST order Arrays.sort(t (a b) -> Integer.compare(a[0] b[0])); // Find minimum swaps by detecting cycles boolean[] visited = new boolean[n]; // Iterate through the array to find cycles for (int i = 0; i < n; i++) { // If the element is already visited or in // the correct place continue if (visited[i] || t[i][1] == i) continue; // Start a cycle and find the number of // nodes in the cycle int cycleSize = 0; int j = i; while (!visited[j]) { visited[j] = true; j = t[j][1]; cycleSize++; } // If there is a cycle we need (cycleSize - 1) // swaps to sort the cycle if (cycleSize > 1) { ans += (cycleSize - 1); } } // Return the total number of swaps return ans; } public static void main(String[] args) { int[] arr = {5 6 7 8 9 10 11}; System.out.println(minSwaps(arr)); } }
# Python program for Minimum swap required # to convert binary tree to binary search tree # Function to perform inorder traversal of the binary tree # and store it in an array def inorder(arr inorderArr index): # If index is out of bounds return n = len(arr) if index >= n: return # Recursively visit left subtree inorder(arr inorderArr 2 * index + 1) # Store current node value in inorderArr inorderArr.append(arr[index]) # Recursively visit right subtree inorder(arr inorderArr 2 * index + 2) # Function to calculate minimum swaps # to sort inorder traversal def minSwaps(arr): inorderArr = [] # Get the inorder traversal of the binary tree inorder(arr inorderArr 0) # Create a list of pairs to store value and original index t = [(inorderArr[i] i) for i in range(len(inorderArr))] ans = 0 # Sort the list of pairs based on values # to get BST order t.sort() # Initialize visited array visited = [False] * len(t) # Find minimum swaps by detecting cycles for i in range(len(t)): # If already visited or already in the # correct place skip if visited[i] or t[i][1] == i: continue # Start a cycle and find the number of # nodes in the cycle cycleSize = 0 j = i # Process all elements in the cycle while not visited[j]: visited[j] = True j = t[j][1] cycleSize += 1 # If there is a cycle of size `cycle_size` we # need `cycle_size - 1` swaps if cycleSize > 1: ans += (cycleSize - 1) # Return total number of swaps return ans if __name__ == '__main__': arr = [5 6 7 8 9 10 11] print(minSwaps(arr))
// C# program for Minimum swap required // to convert binary tree to binary search tree using System; using System.Linq; class GfG { // Function to perform inorder traversal of the binary tree // and store it in an array static void Inorder(int[] arr int[] inorderArr int index ref int counter) { int n = arr.Length; // Base case: if index is out of bounds return if (index >= n) return; // Recursively visit left subtree Inorder(arr inorderArr 2 * index + 1 ref counter); // Store current node value in inorderArr inorderArr[counter] = arr[index]; counter++; // Recursively visit right subtree Inorder(arr inorderArr 2 * index + 2 ref counter); } // Function to calculate minimum // swaps to sort inorder traversal static int MinSwaps(int[] arr) { int n = arr.Length; int[] inorderArr = new int[n]; int counter = 0; // Get the inorder traversal of the binary tree Inorder(arr inorderArr 0 ref counter); // Create an array of pairs to store value // and original index var t = new (int int)[n]; for (int i = 0; i < n; i++) { t[i] = (inorderArr[i] i); } // Sort the array based on values to get BST order Array.Sort(t (a b) => a.Item1.CompareTo(b.Item1)); // Initialize visited array bool[] visited = new bool[n]; int ans = 0; // Find minimum swaps by detecting cycles for (int i = 0; i < n; i++) { // If already visited or already in // the correct place skip if (visited[i] || t[i].Item2 == i) continue; // Start a cycle and find the number // of nodes in the cycle int cycleSize = 0; int j = i; // Process all elements in the cycle while (!visited[j]) { visited[j] = true; j = t[j].Item2; cycleSize++; } // If there is a cycle of size `cycle_size` we // need `cycle_size - 1` swaps if (cycleSize > 1) { ans += (cycleSize - 1); } } // Return total number of swaps return ans; } static void Main(string[] args) { int[] arr = { 5 6 7 8 9 10 11 }; Console.WriteLine(MinSwaps(arr)); } }
// Javascript program for Minimum swap required // to convert binary tree to binary search tree // Inorder traversal to get values in sorted order function inorder(arr inorderArr index) { // If index is out of bounds return if (index >= arr.length) return; // Recursively visit left subtree inorder(arr inorderArr 2 * index + 1); // Store current node value in array inorderArr.push(arr[index]); // Recursively visit right subtree inorder(arr inorderArr 2 * index + 2); } // Function to calculate minimum swaps to sort inorder // traversal function minSwaps(arr) { let inorderArr = []; // Get the inorder traversal of the binary tree inorder(arr inorderArr 0); // Create an array of pairs to store value and original // index let t = inorderArr.map((val i) => [val i]); let ans = 0; // Sort the pair array based on values to get BST order t.sort((a b) => a[0] - b[0]); // Find minimum swaps by detecting cycles let visited = Array(arr.length) .fill(false); for (let i = 0; i < t.length; i++) { // If the element is already in the correct // position continue if (visited[i] || t[i][1] === i) continue; // Otherwise perform swaps until the element is in // the right place let cycleSize = 0; let j = i; while (!visited[j]) { visited[j] = true; j = t[j][1]; cycleSize++; } // If there is a cycle we need (cycleSize - 1) // swaps to sort the cycle if (cycleSize > 1) { ans += (cycleSize - 1); } } // Return total number of swaps return ans; } let arr = [ 5 6 7 8 9 10 11 ]; console.log(minSwaps(arr));
Uitvoer
3
Tijdcomplexiteit: O(n*logn) waar N is het aantal elementen in de array.
Hulpruimte: O(n) omdat het extra ruimte gebruikt voor array
wiskunde pow java
Oefening: Kunnen we dit uitbreiden naar een normale binaire boom, dat wil zeggen een binaire boom die wordt weergegeven met behulp van linker- en rechteraanwijzers en die niet noodzakelijkerwijs compleet is?
Quiz maken



