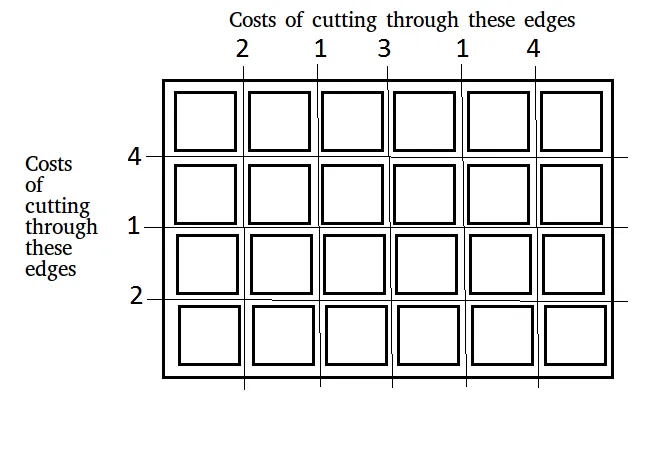
Gegeven een bord met afmetingen n × m dat in n x m vierkanten moet worden gesneden. De kosten voor het maken van een snede langs een horizontale of verticale rand worden in twee reeksen weergegeven:

• X[] : Kostenbesparing langs de verticale randen (in de lengte).
• En[] : Kostenbesparing langs de horizontale randen (in de breedte).

Vind de minimale totale kosten die nodig zijn om het bord optimaal in vierkanten te snijden.

Voorbeelden: 

Invoer: x[] = [2 1 3 1 4] y[] = [4 1 2] n = 4 m = 6
Uitgang: 42
Uitleg:

Aanvankelijk nee. van horizontale segmenten = 1 & nee. van verticale segmenten = 1.
De optimale manier om in vierkant te snijden is:
Kies 4 (uit x) -> verticale snede Kosten = 4 × horizontale segmenten = 4
 Nu horizontale segmenten = 1 verticale segmenten = 2.
Kies 4 (vanaf y) -> horizontale snede Kosten = 4 × verticale segmenten = 8
 Nu horizontale segmenten = 2 verticale segmenten = 2.
Kies 3 (uit x) -> verticale snede Kosten = 3 × horizontale segmenten = 6
 Nu horizontale segmenten = 2 verticale segmenten = 3.
Kies 2 (uit x) -> verticale snede Kosten = 2 × horizontale segmenten = 4
 Nu horizontale segmenten = 2 verticale segmenten = 4.
Kies 2 (vanaf y) -> horizontale snede Kosten = 2 × verticale segmenten = 8
 Nu horizontale segmenten = 3 verticale segmenten = 4.
Kies 1 (uit x) -> verticale snede Kosten = 1 × horizontale segmenten = 3
Nu horizontale segmenten = 3 verticale segmenten = 5.
Kies 1 (uit x) -> verticale snede Kosten = 1 × horizontale segmenten = 3
Nu horizontale segmenten = 3 verticale segmenten = 6.
Kies 1 (vanaf y) -> horizontale snede Kosten = 1 × verticale segmenten = 6
Nu horizontale segmenten = 4 verticale segmenten = 6.
Dus de totale kosten = 4 + 8 + 6 + 4 + 8 + 3 + 3 + 6 = 42.

Invoer: x[] = [1 1 1] y[] = [1 1 1] n = 4 m = 4
Uitgang: 15
Uitleg:
Aanvankelijk nee. van horizontale segmenten = 1 & nee. van verticale segmenten = 1.
De optimale manier om in vierkant te snijden is:
Kies 1 (vanaf y) -> horizontale snede Kosten = 1 × verticale segmenten = 1
Nu horizontale segmenten = 2 verticale segmenten = 1.
Kies 1 (vanaf y) -> horizontale snede Kosten = 1 × verticale segmenten = 1
Nu horizontale segmenten = 3 verticale segmenten = 1.
Kies 1 (vanaf y) -> horizontale snede Kosten = 1 × verticale segmenten = 1
Nu horizontale segmenten = 4 verticale segmenten = 1.
Kies 1 (uit x) -> verticale snede Kosten = 1 × horizontale segmenten = 4
Nu horizontale segmenten = 4 verticale segmenten = 2.
Kies 1 (uit x) -> verticale snede Kosten = 1 × horizontale segmenten = 4
Nu horizontale segmenten = 4 verticale segmenten = 3.
Kies 1 (uit x) -> verticale snede Kosten = 1 × horizontale segmenten = 4
Nu horizontale segmenten = 4 verticale segmenten = 4
Dus de totale kosten = 1 + 1 + 1 + 4 + 4 + 4 = 15.

Inhoudsopgave

• [Naïeve aanpak] Probeer alle permutaties - O((n+m)!×(n+m)) Tijd en O(n+m) Ruimte
• [Verwachte aanpak] Greedy-techniek gebruiken - O( n (log n)+m (log m)) Tijd en O(1) Ruimte

[Naïeve aanpak] Probeer alle permutaties - O((n+m)!×(n+m)) Tijd en O(n+m) Ruimte

Het idee is om alle mogelijke permutaties van de gegeven bezuinigingen te genereren en vervolgens de kosten voor elke permutatie te berekenen. Geef ten slotte de minimale kosten onder hen terug.

Opmerking: Deze aanpak is niet haalbaar voor grotere inputs, omdat het aantal permutaties factorieel groeit als (m+n-2)!.
Voor elke permutatie moeten we de kosten in O(m+n) tijd berekenen. De totale tijdscomplexiteit wordt dus O((m+n−2)!×(m+n)).

[Verwachte aanpak] Greedy-techniek gebruiken - O( n (log n)+m (log m)) Tijd en O(1) Ruimte

Het idee is om eerst de duurste bezuinigingen uit te voeren met behulp van een hebzuchtige aanpak . De observatie is dat het kiezen van de hoogste kostenbesparing bij elke stap de toekomstige kosten verlaagt doordat meerdere onderdelen tegelijk worden beïnvloed. We sorteren de verticale (x) en horizontale (y) kosten in aflopende volgorde en kiezen vervolgens iteratief de grotere om de kostenbesparingen te maximaliseren. De resterende sneden worden afzonderlijk verwerkt om ervoor te zorgen dat alle secties optimaal worden gesplitst.

Wat gebeurt er als we bezuinigen?

• Horizontale snede → je snijdt over de breedte zodat het aantal horizontale stroken toeneemt (hCount++). Maar de kosten worden vermenigvuldigd met vCount (het aantal verticale stroken) omdat de horizontale snede door alle verticale segmenten moet gaan.
• Verticale snede → je snijdt over de hoogte zodat het aantal verticale stroken toeneemt (vCount++). Maar de kosten worden vermenigvuldigd met hCount (het aantal horizontale stroken), omdat de verticale snede door alle horizontale segmenten moet gaan.

Stappen om het probleem op te lossen:

• Sorteer zowel x- als y-arrays in aflopende volgorde.
• Gebruik twee aanwijzers, één voor x en één voor y, beginnend bij de grootste waarde en richting kleinere waarden.
• Onderhoud hCount en vCount om bij te houden hoeveel segmenten elke verlaging beïnvloedt en update deze dienovereenkomstig.
• Herhaal dit terwijl zowel x als y onverwerkte bezuinigingen hebben, waarbij u altijd de hogere kosten kiest om de totale kosten te minimaliseren.
• Als x nog resterende bezuinigingen heeft, verwerk deze dan met de hCount-vermenigvuldiger; Verwerk op dezelfde manier de resterende y-sneden met vCount.
• Bereken de totale kosten bij elke stap met behulp van de formule: kosten verlagen * aantal getroffen onderdelen, waardoor de kosten minimaal zijn.

#include   #include #include   using namespace std; int minCost(int n int m   vector<int>& x vector<int>& y) {    // Sort the cutting costs in ascending order  sort(x.begin() x.end());  sort(y.begin() y.end());   int hCount = 1 vCount = 1;   int i = x.size() - 1 j = y.size() - 1;   int totalCost = 0;  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;   vCount++;  i--;  }   else {  totalCost += y[j] * vCount;   hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost; } int main() {    int n = 4 m = 6;  vector<int> x = {2 1 3 1 4};  vector<int> y = {4 1 2};  cout << minCost(n m x y) << endl;  return 0; } 

import java.util.Arrays; class GfG {    static int minCost(int n int m   int[] x int[] y) {    // Sort the cutting costs in ascending order  Arrays.sort(x);  Arrays.sort(y);   int hCount = 1 vCount = 1;   int i = x.length - 1 j = y.length - 1;   int totalCost = 0;  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;   vCount++;  i--;  }   else {  totalCost += y[j] * vCount;   hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost;  }  public static void main(String[] args) {    int n = 4m = 6;  int[] x = {2 1 3 1 4};  int[] y = {4 1 2};  System.out.println(minCost(n m x y));  } } 

def minCost(nm x y): # Sort the cutting costs in ascending order x.sort() y.sort() hCount vCount = 1 1 i j = len(x) - 1 len(y) - 1 totalCost = 0 while i >= 0 and j >= 0: # Choose the larger cost cut to  # minimize future costs if x[i] >= y[j]: totalCost += x[i] * hCount vCount += 1 i -= 1 else: totalCost += y[j] * vCount hCount += 1 j -= 1 # Process remaining vertical cuts while i >= 0: totalCost += x[i] * hCount vCount += 1 i -= 1 # Process remaining horizontal cuts while j >= 0: totalCost += y[j] * vCount hCount += 1 j -= 1 return totalCost if __name__ == '__main__': nm = 4 6 x = [2 1 3 1 4] y = [4 1 2] print(minCost(nmx y)) 

using System; class GfG {  public static int minCost(int n int m   int[] x int[] y) {    // Sort the cutting costs in ascending order  Array.Sort(x);  Array.Sort(y);  int hCount = 1 vCount = 1;  int i = x.Length - 1 j = y.Length - 1;  int totalCost = 0;  // Process the cuts in greedy manner  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  else {  totalCost += y[j] * vCount;  hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost;  }    public static void Main() {    int n=4m=6;  int[] x = {2 1 3 1 4};  int[] y = {4 1 2};  Console.WriteLine(minCost(nm x y));  } } 

function minCost( nm x y) {    // Sort the cutting costs in ascending order  x.sort((a b) => a - b);  y.sort((a b) => a - b);  let hCount = 1 vCount = 1;  let i = x.length - 1 j = y.length - 1;  let totalCost = 0;  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;  vCount++;  i--;  }   else {  totalCost += y[j] * vCount;  hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost; } // Driver Code let n = 4m = 6; let x = [2 1 3 1 4]; let y = [4 1 2]; console.log(minCost(nm x y)); 

42