Het Luhn-algoritme, ook wel bekend als het module 10 of richting 10 algoritme, is een eenvoudige controlesomformule die wordt gebruikt om een verscheidenheid aan identificatienummers te valideren, zoals creditcardnummers, IMEI-nummers en Canadese socialezekerheidsnummers. De LUHN-formule werd eind jaren zestig bedacht door een groep wiskundigen. Kort daarna adopteerden creditcardmaatschappijen het. Omdat het algoritme zich in het publieke domein bevindt, kan het door iedereen worden gebruikt. De meeste creditcards en veel overheidsidentificatienummers gebruiken het algoritme als een eenvoudige methode om geldige nummers te onderscheiden van verkeerd getypte of anderszins onjuiste nummers. Het is ontworpen om te beschermen tegen onbedoelde fouten, niet tegen kwaadaardige aanvallen.
Stappen die betrokken zijn bij het Luhn-algoritme
Laten we het algoritme begrijpen met een voorbeeld:
Neem het voorbeeld van een rekeningnummer 79927398713 .
Stap 1 – Begin vanaf het meest rechtse cijfer en verdubbel de waarde van elk tweede cijfer,
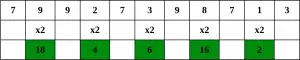
Stap 2 – Als de verdubbeling van een getal resulteert in een getal van twee cijfers, d.w.z. groter dan 9 (bijvoorbeeld 6 × 2 = 12), tel dan de cijfers van het product op (bijvoorbeeld 12: 1 + 2 = 3, 15: 1 + 5 = 6), om een getal van één cijfer te krijgen.

Stap 3 – Neem nu de som van alle cijfers.
Java-gebruikersinvoer

Stap 4 – Als het totaal modulo 10 gelijk is aan 0 (als het totaal op nul eindigt), dan is het getal geldig volgens de Luhn-formule; anders is het niet geldig.

Omdat de som 70 is, wat een veelvoud is van 10, is het rekeningnummer mogelijk geldig.
Het idee is simpel; we doorkruisen vanaf het einde. Voor elk tweede cijfer verdubbelen we het voordat we het toevoegen. We voegen twee cijfers toe van het getal dat wordt verkregen na verdubbeling.
Implementatie:
C++
// C++ program to implement Luhn algorithm> #include> using> namespace> std;> // Returns true if given card number is valid> bool> checkLuhn(>const> string& cardNo)> {> >int> nDigits = cardNo.length();> >int> nSum = 0, isSecond =>false>;> >for> (>int> i = nDigits - 1; i>= 0; ik--) {> >int> d = cardNo[i] ->'0'>;> >if> (isSecond ==>true>)> >d = d * 2;> >// We add two digits to handle> >// cases that make two digits after> >// doubling> >nSum += d / 10;> >nSum += d % 10;> >isSecond = !isSecond;> >}> >return> (nSum % 10 == 0);> }> // Driver code> int> main()> {> >string cardNo =>'79927398713'>;> >if> (checkLuhn(cardNo))> >printf>(>'This is a valid card'>);> >else> >printf>(>'This is not a valid card'>);> >return> 0;> }> |
>
>
Java
// Java program to implement> // Luhn algorithm> import> java.io.*;> class> GFG {> > // Returns true if given> // card number is valid> static> boolean> checkLuhn(String cardNo)> {> >int> nDigits = cardNo.length();> >int> nSum =>0>;> >boolean> isSecond =>false>;> >for> (>int> i = nDigits ->1>; i>=>0>; i--)> >{> >int> d = cardNo.charAt(i) ->'0'>;> >if> (isSecond ==>true>)> >d = d *>2>;> >// We add two digits to handle> >// cases that make two digits> >// after doubling> >nSum += d />10>;> >nSum += d %>10>;> >isSecond = !isSecond;> >}> >return> (nSum %>10> ==>0>);> }> >// Driver code> >static> public> void> main (String[] args)> >{> >String cardNo =>'79927398713'>;> >if> (checkLuhn(cardNo))> >System.out.println(>'This is a valid card'>);> >else> >System.out.println(>'This is not a valid card'>);> > >}> }> // This Code is contributed by vt_m.> |
voetnoten afwaardering
>
>
Python3
# Python3 program to implement> # Luhn algorithm> # Returns true if given card> # number is valid> def> checkLuhn(cardNo):> > >nDigits>=> len>(cardNo)> >nSum>=> 0> >isSecond>=> False> > >for> i>in> range>(nDigits>-> 1>,>->1>,>->1>):> >d>=> ord>(cardNo[i])>-> ord>(>'0'>)> > >if> (isSecond>=>=> True>):> >d>=> d>*> 2> > ># We add two digits to handle> ># cases that make two digits after> ># doubling> >nSum>+>=> d>/>/> 10> >nSum>+>=> d>%> 10> > >isSecond>=> not> isSecond> > >if> (nSum>%> 10> =>=> 0>):> >return> True> >else>:> >return> False> # Driver code> if> __name__>=>=>'__main__'>:> > >cardNo>=> '79927398713'> > >if> (checkLuhn(cardNo)):> >print>(>'This is a valid card'>)> >else>:> >print>(>'This is not a valid card'>)> # This code is contributed by rutvik_56> |
>
>
C#
hoe je een Beats-hoofdtelefoon koppelt
// C# program to implement> // Luhn algorithm> using> System;> class> GFG {> > // Returns true if given> // card number is valid> static> bool> checkLuhn(String cardNo)> {> >int> nDigits = cardNo.Length;> >int> nSum = 0;> >bool> isSecond =>false>;> >for> (>int> i = nDigits - 1; i>= 0; ik--)> >{> >int> d = cardNo[i] ->'0'>;> >if> (isSecond ==>true>)> >d = d * 2;> >// We add two digits to handle> >// cases that make two digits> >// after doubling> >nSum += d / 10;> >nSum += d % 10;> >isSecond = !isSecond;> >}> >return> (nSum % 10 == 0);> }> >// Driver code> >static> public> void> Main()> >{> >String cardNo =>'79927398713'>;> >if> (checkLuhn(cardNo))> >Console.WriteLine(>'This is a valid card'>);> >else> >Console.WriteLine(>'This is not a valid card'>);> > >}> }> // This Code is contributed by vt_m.> |
>
string.replaceall java
>
Javascript
> >// Javascript program to implement Luhn algorithm> > >// Returns true if given> >// card number is valid> >function> checkLuhn(cardNo)> >{> >let nDigits = cardNo.length;> >let nSum = 0;> >let isSecond =>false>;> >for> (let i = nDigits - 1; i>= 0; ik--)> >{> >let d = cardNo[i].charCodeAt() ->'0'>.charCodeAt();> >if> (isSecond ==>true>)> >d = d * 2;> >// We add two digits to handle> >// cases that make two digits> >// after doubling> >nSum += parseInt(d / 10, 10);> >nSum += d % 10;> >isSecond = !isSecond;> >}> >return> (nSum % 10 == 0);> >}> > >let cardNo =>'79927398713'>;> >if> (checkLuhn(cardNo))> >document.write(>'This is a valid card'>);> >else> >document.write(>'This is not a valid card'>);> > > |
>
>Uitvoer
This is a valid card>
Het Luhn-algoritme detecteert elke fout van één cijfer, evenals bijna alle transposities van aangrenzende cijfers.
