Gegeven twee strings ‘X’ en ‘Y’, zoek de lengte van de langste gemeenschappelijke substring.
Voorbeelden:
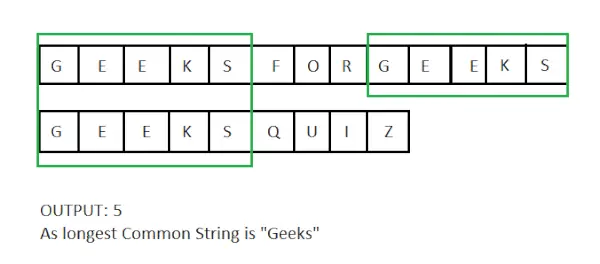
Invoer : X = techcodeview.com, y = GeeksQuiz
Uitvoer : 5
Uitleg:
De langste gemeenschappelijke subtekenreeks is Geeks en heeft een lengte van 5.
Invoer : X = abcdxyz, y = xyzabcd
Uitgang: 4
Uitleg:
De langste gemeenschappelijke subtekenreeks is abcd en heeft een lengte van 4.Invoer : X = zxabcdezy, y = yzabcdezx
Uitgang: 6
Uitleg:
De langste gemeenschappelijke subtekenreeks is abcdez en heeft een lengte van 6.
Benadering:
Laat m en n respectievelijk de lengten zijn van de eerste en tweede reeks.
A eenvoudige oplossing is om één voor één alle substrings van de eerste string te bekijken en voor elke substring te controleren of het een substring in de tweede string is. Houd de maximale lengte van de substring bij. Er zullen O(m^2) substrings zijn en we kunnen in O(n) tijd ontdekken of een string een substring is op een andere string (zie dit ). De totale tijdscomplexiteit van deze methode zou dus O(n * m zijn2)
Dynamisch programmeren kan worden gebruikt om de langste gemeenschappelijke substring in O(m*n) tijd te vinden. Het idee is om de lengte van het langste algemene achtervoegsel voor alle substrings van beide strings te vinden en deze lengtes in een tabel op te slaan.
Het langste algemene achtervoegsel heeft de volgende optimale onderbouweigenschap.
structuur in de datastructuurAls de laatste tekens overeenkomen, verminderen we beide lengtes met 1
- LCSuff(X, Y, m, n) = LCSuff(X, Y, m-1, n-1) + 1 als X[m-1] = Y[n-1]
Als de laatste tekens niet overeenkomen, is het resultaat 0, d.w.z.
- LCSuff(X, Y, m, n) = 0 als (X[m-1] != Y[n-1])
Nu beschouwen we achtervoegsels van verschillende substrings die eindigen op verschillende indexen.
De maximale lengte van het langste gemeenschappelijke achtervoegsel is de langste gemeenschappelijke subtekenreeks.
LCSubStr(X, Y, m, n) = Max(LCSuff(X, Y, i, j)) waarbij 1 <= i <= m en 1 <= j <= n
Hieronder volgt de iteratieve implementatie van de bovenstaande oplossing.
C++
/* Dynamic Programming solution to> >find length of the> >longest common substring */> #include> #include> using> namespace> std;> /* Returns length of longest> >common substring of X[0..m-1]> >and Y[0..n-1] */> int> LCSubStr(>char>* X,>char>* Y,>int> m,>int> n)> {> >// Create a table to store> >// lengths of longest> >// common suffixes of substrings.> >// Note that LCSuff[i][j] contains> >// length of longest common suffix> >// of X[0..i-1] and Y[0..j-1].> >int> LCSuff[m + 1][n + 1];> >int> result = 0;>// To store length of the> >// longest common substring> >/* Following steps build LCSuff[m+1][n+1] in> >bottom up fashion. */> >for> (>int> i = 0; i <= m; i++)> >{> >for> (>int> j = 0; j <= n; j++)> >{> >// The first row and first column> >// entries have no logical meaning,> >// they are used only for simplicity> >// of program> >if> (i == 0 || j == 0)> >LCSuff[i][j] = 0;> >else> if> (X[i - 1] == Y[j - 1]) {> >LCSuff[i][j] = LCSuff[i - 1][j - 1] + 1;> >result = max(result, LCSuff[i][j]);> >}> >else> >LCSuff[i][j] = 0;> >}> >}> >return> result;> }> // Driver code> int> main()> {> >char> X[] =>'OldSite:techcodeview.com.org'>;> >char> Y[] =>'NewSite:GeeksQuiz.com'>;> >int> m =>strlen>(X);> >int> n =>strlen>(Y);> >cout <<>'Length of Longest Common Substring is '> ><< LCSubStr(X, Y, m, n);> >return> 0;> }> |
>
>
Java
// Java implementation of> // finding length of longest> // Common substring using> // Dynamic Programming> import> java.io.*;> class> GFG {> >/*> >Returns length of longest common substring> >of X[0..m-1] and Y[0..n-1]> >*/> >static> int> LCSubStr(>char> X[],>char> Y[],>int> m,>int> n)> >{> >// Create a table to store> >// lengths of longest common> >// suffixes of substrings.> >// Note that LCSuff[i][j]> >// contains length of longest> >// common suffix of> >// X[0..i-1] and Y[0..j-1].> >// The first row and first> >// column entries have no> >// logical meaning, they are> >// used only for simplicity of program> >int> LCStuff[][] =>new> int>[m +>1>][n +>1>];> >// To store length of the longest> >// common substring> >int> result =>0>;> >// Following steps build> >// LCSuff[m+1][n+1] in bottom up fashion> >for> (>int> i =>0>; i <= m; i++) {> >for> (>int> j =>0>; j <= n; j++) {> >if> (i ==>0> || j ==>0>)> >LCStuff[i][j] =>0>;> >else> if> (X[i ->1>] == Y[j ->1>]) {> >LCStuff[i][j]> >= LCStuff[i ->1>][j ->1>] +>1>;> >result = Integer.max(result,> >LCStuff[i][j]);> >}> >else> >LCStuff[i][j] =>0>;> >}> >}> >return> result;> >}> >// Driver Code> >public> static> void> main(String[] args)> >{> >String X =>'OldSite:techcodeview.com.org'>;> >String Y =>'NewSite:GeeksQuiz.com'>;> >int> m = X.length();> >int> n = Y.length();> >System.out.println(> >'Length of Longest Common Substring is '> >+ LCSubStr(X.toCharArray(), Y.toCharArray(), m,> >n));> >}> }> // This code is contributed by Sumit Ghosh> |
>
>
Python3
# Python3 implementation of Finding> # Length of Longest Common Substring> # Returns length of longest common> # substring of X[0..m-1] and Y[0..n-1]> def> LCSubStr(X, Y, m, n):> ># Create a table to store lengths of> ># longest common suffixes of substrings.> ># Note that LCSuff[i][j] contains the> ># length of longest common suffix of> ># X[0...i-1] and Y[0...j-1]. The first> ># row and first column entries have no> ># logical meaning, they are used only> ># for simplicity of the program.> ># LCSuff is the table with zero> ># value initially in each cell> >LCSuff>=> [[>0> for> k>in> range>(n>+>1>)]>for> l>in> range>(m>+>1>)]> ># To store the length of> ># longest common substring> >result>=> 0> ># Following steps to build> ># LCSuff[m+1][n+1] in bottom up fashion> >for> i>in> range>(m>+> 1>):> >for> j>in> range>(n>+> 1>):> >if> (i>=>=> 0> or> j>=>=> 0>):> >LCSuff[i][j]>=> 0> >elif> (X[i>->1>]>=>=> Y[j>->1>]):> >LCSuff[i][j]>=> LCSuff[i>->1>][j>->1>]>+> 1> >result>=> max>(result, LCSuff[i][j])> >else>:> >LCSuff[i][j]>=> 0> >return> result> # Driver Code> X>=> 'OldSite:techcodeview.com.org'> Y>=> 'NewSite:GeeksQuiz.com'> m>=> len>(X)> n>=> len>(Y)> print>(>'Length of Longest Common Substring is'>,> >LCSubStr(X, Y, m, n))> # This code is contributed by Soumen Ghosh> |
nullpointerexception
>
>
C#
// C# implementation of finding length of longest> // Common substring using Dynamic Programming> using> System;> class> GFG {> >// Returns length of longest common> >// substring of X[0..m-1] and Y[0..n-1]> >static> int> LCSubStr(>string> X,>string> Y,>int> m,>int> n)> >{> >// Create a table to store lengths of> >// longest common suffixes of substrings.> >// Note that LCSuff[i][j] contains length> >// of longest common suffix of X[0..i-1]> >// and Y[0..j-1]. The first row and first> >// column entries have no logical meaning,> >// they are used only for simplicity of> >// program> >int>[, ] LCStuff =>new> int>[m + 1, n + 1];> >// To store length of the longest common> >// substring> >int> result = 0;> >// Following steps build LCSuff[m+1][n+1]> >// in bottom up fashion> >for> (>int> i = 0; i <= m; i++)> >{> >for> (>int> j = 0; j <= n; j++)> >{> >if> (i == 0 || j == 0)> >LCStuff[i, j] = 0;> >else> if> (X[i - 1] == Y[j - 1])> >{> >LCStuff[i, j]> >= LCStuff[i - 1, j - 1] + 1;> >result> >= Math.Max(result, LCStuff[i, j]);> >}> >else> >LCStuff[i, j] = 0;> >}> >}> >return> result;> >}> >// Driver Code> >public> static> void> Main()> >{> >String X =>'OldSite:techcodeview.com.org'>;> >String Y =>'NewSite:GeeksQuiz.com'>;> >int> m = X.Length;> >int> n = Y.Length;> >Console.Write(>'Length of Longest Common'> >+>' Substring is '> >+ LCSubStr(X, Y, m, n));> >}> }> // This code is contributed by Sam007.> |
>
>
Javascript
> // JavaScript implementation of> // finding length of longest> // Common substring using> // Dynamic Programming> >/*> >Returns length of longest common> >substring of X[0..m-1] and Y[0..n-1]> >*/> >function> LCSubStr( X, Y , m , n) {> >// Create a table to store> >// lengths of longest common> >// suffixes of substrings.> >// Note that LCSuff[i][j]> >// contains length of longest> >// common suffix of> >// X[0..i-1] and Y[0..j-1].> >// The first row and first> >// column entries have no> >// logical meaning, they are> >// used only for simplicity of program> > >var> LCStuff => >Array(m + 1).fill().map(()=>Array(n + 1).fill(0));> >// To store length of the longest> >// common substring> >var> result = 0;> >// Following steps build> >// LCSuff[m+1][n+1] in bottom up fashion> >for> (i = 0; i <= m; i++) {> >for> (j = 0; j <= n; j++) {> >if> (i == 0 || j == 0)> >LCStuff[i][j] = 0;> >else> if> (X[i - 1] == Y[j - 1]) {> >LCStuff[i][j] = LCStuff[i - 1][j - 1] + 1;> >result = Math.max(result, LCStuff[i][j]);> >}>else> >LCStuff[i][j] = 0;> >}> >}> >return> result;> >}> >// Driver Code> > >var> X =>'OldSite:techcodeview.com.org'>;> >var> Y =>'NewSite:GeeksQuiz.com'>;> >var> m = X.length;> >var> n = Y.length;> >document.write(>'Length of Longest Common Substring is '> +> >LCSubStr(X, Y, m, n));> // This code contributed by Rajput-Ji> > |
>
>
PHP
// Dynamic Programming solution to find // length of the longest common substring // Returns length of longest common // substring of X[0..m-1] and Y[0..n-1] function LCSubStr($X, $Y, $m, $n) { // Create a table to store lengths of // longest common suffixes of substrings. // Notethat LCSuff[i][j] contains length // of longest common suffix of X[0..i-1] // and Y[0..j-1]. The first row and // first column entries have no logical // meaning, they are used only for // simplicity of program $LCSuff = array_fill(0, $m + 1, array_fill(0, $n + 1, NULL)); $result = 0; // To store length of the // longest common substring // Following steps build LCSuff[m+1][n+1] // in bottom up fashion. for ($i = 0; $i <= $m; $i++) { for ($j = 0; $j <= $n; $j++) { if ($i == 0 || $j == 0) $LCSuff[$i][$j] = 0; else if ($X[$i - 1] == $Y[$j - 1]) { $LCSuff[$i][$j] = $LCSuff[$i - 1][$j - 1] + 1; $result = max($result, $LCSuff[$i][$j]); } else $LCSuff[$i][$j] = 0; } } return $result; } // Driver Code $X = 'OldSite:techcodeview.com.org'; $Y = 'NewSite:GeeksQuiz.com'; $m = strlen($X); $n = strlen($Y); echo 'Length of Longest Common Substring is ' . LCSubStr($X, $Y, $m, $n); // This code is contributed by ita_c ?>> |
>
>Uitvoer
Length of Longest Common Substring is 10>
Tijdcomplexiteit: O(m*n)
Hulpruimte: O(m*n), aangezien m*n extra ruimte is ingenomen.
Een andere aanpak: (Ruimte-geoptimaliseerde aanpak).
In de bovenstaande benadering gebruiken we alleen de laatste rij van de 2D-array, daarom kunnen we de ruimte optimaliseren door gebruik te maken van
een 2D-array met afmeting 2*(min(n,m)).
Hieronder vindt u de implementatie van de bovenstaande aanpak:
C++
#include> #include> using> namespace> std;> // Function to find the length of the longest LCS> int> LCSubStr(string s, string t,>int> n,>int> m)> {> >// Create DP table> >vectorint>> dp(n + 1, vector |
>
>
Java
// Java implementation of the above approach> import> java.io.*;> class> GFG> {> > >// Function to find the length of the> >// longest LCS> >static> int> LCSubStr(String s,String t,> >int> n,>int> m)> >{> > >// Create DP table> >int> dp[][]=>new> int>[>2>][m+>1>];> >int> res=>0>;> > >for>(>int> i=>1>;i<=n;i++)> >{> >for>(>int> j=>1>;j<=m;j++)> >{> >if>(s.charAt(i->1>)==t.charAt(j->1>))> >{> >dp[i%>2>][j]=dp[(i->1>)%>2>][j->1>]+>1>;> >if>(dp[i%>2>][j]>res)> >res=dp[i%>2>][j];> >}> >else> dp[i%>2>][j]=>0>;> >}> >}> >return> res;> >}> > >// Driver Code> >public> static> void> main (String[] args)> >{> >String X=>'OldSite:techcodeview.com.org'>;> >String Y=>'NewSite:GeeksQuiz.com'>;> > >int> m=X.length();> >int> n=Y.length();> > >// Function call> >System.out.println(LCSubStr(X,Y,m,n));> > >}> }> |
>
>
Python3
systeem software
# Python implementation of the above approach> # Function to find the length of the> # longest LCS> def> LCSubStr(s, t, n, m):> > ># Create DP table> >dp>=> [[>0> for> i>in> range>(m>+> 1>)]>for> j>in> range>(>2>)]> >res>=> 0> > >for> i>in> range>(>1>,n>+> 1>):> >for> j>in> range>(>1>,m>+> 1>):> >if>(s[i>-> 1>]>=>=> t[j>-> 1>]):> >dp[i>%> 2>][j]>=> dp[(i>-> 1>)>%> 2>][j>-> 1>]>+> 1> >if>(dp[i>%> 2>][j]>res):> >res>=> dp[i>%> 2>][j]> >else>:> >dp[i>%> 2>][j]>=> 0> >return> res> # Driver Code> X>=> 'OldSite:techcodeview.com.org'> Y>=> 'NewSite:GeeksQuiz.com'> m>=> len>(X)> n>=> len>(Y)> # Function call> print>(LCSubStr(X,Y,m,n))> # This code is contributed by avanitrachhadiya2155> |
>
>
C#
// C# implementation of the above approach> using> System;> public> class> GFG> {> >// Function to find the length of the> >// longest LCS> >static> int> LCSubStr(>string> s,>string> t,> >int> n,>int> m)> >{> >// Create DP table> >int>[,] dp =>new> int>[2, m + 1];> >int> res = 0;> >for>(>int> i = 1; i <= n; i++)> >{> >for>(>int> j = 1; j <= m; j++)> >{> >if>(s[i - 1] == t[j - 1])> >{> >dp[i % 2, j] = dp[(i - 1) % 2, j - 1] + 1;> >if>(dp[i % 2, j]>res)> >res = dp[i % 2, j];> >}> >else> dp[i % 2, j] = 0;> >}> >}> >return> res;> >}> >// Driver Code> >static> public> void> Main (){> >string> X =>'OldSite:techcodeview.com.org'>;> >string> Y =>'NewSite:GeeksQuiz.com'>;> >int> m = X.Length;> >int> n = Y.Length;> >// Function call> >Console.WriteLine(LCSubStr(X,Y,m,n));> >}> }> // This code is contributed by rag2127> |
>
>
Javascript
> // JavaScript implementation of the above approach> >// Function to find the length of the> >// longest LCS> >function> LCSubStr(s, t, n, m)> >{> > >// Create DP table> >var> dp = Array(2).fill().map(()=>Array(m+ 1).fill(0));> >var> res = 0;> > >for>(>var> i = 1; i <= n; i++)> >{> >for>(>var> j = 1; j <= m; j++)> >{> >if>(s.charAt(i - 1) == t.charAt(j - 1))> >{> >dp[i % 2][j] = dp[(i - 1) % 2][j - 1] + 1;> >if>(dp[i % 2][j]>res)> >res = dp[i % 2][j];> >}> >else> dp[i % 2][j] = 0;> >}> >}> >return> res;> >}> > >// Driver Code> >var> X =>'OldSite:techcodeview.com.org'>;> >var> Y =>'NewSite:GeeksQuiz.com'>;> > >var> m = X.length;> >var> n = Y.length;> > >// Function call> >document.write(LCSubStr(X, Y, m, n));> // This code is contributed by shivanisinghss2110> > |
>
>Uitvoer
10>
Tijdcomplexiteit: O(n*m)
Hulpruimte: O(min(m,n))
Een andere aanpak: (Recursie gebruiken)
Hier is de recursieve oplossing van de bovenstaande benadering.
C++
aw java
// C++ program using to find length of the> // longest common substring recursion> #include> using> namespace> std;> string X, Y;> // Returns length of function f> // or longest common substring> // of X[0..m-1] and Y[0..n-1]> int> lcs(>int> i,>int> j,>int> count)> {> >if> (i == 0 || j == 0)> >return> count;> >if> (X[i - 1] == Y[j - 1]) {> >count = lcs(i - 1, j - 1, count + 1);> >}> >count = max(count,> >max(lcs(i, j - 1, 0),> >lcs(i - 1, j, 0)));> >return> count;> }> // Driver code> int> main()> {> >int> n, m;> >X =>'abcdxyz'>;> >Y =>'xyzabcd'>;> >n = X.size();> >m = Y.size();> >cout << lcs(n, m, 0);> >return> 0;> }> |
>
>
Java
// Java program using to find length of the> // longest common substring recursion> import> java.io.*;> class> GFG {> >static> String X, Y;> >// Returns length of function> >// for longest common> >// substring of X[0..m-1] and Y[0..n-1]> >static> int> lcs(>int> i,>int> j,>int> count)> >{> >if> (i ==>0> || j ==>0>)> >{> >return> count;> >}> >if> (X.charAt(i ->1>)> >== Y.charAt(j ->1>))> >{> >count = lcs(i ->1>, j ->1>, count +>1>);> >}> >count = Math.max(count,> >Math.max(lcs(i, j ->1>,>0>),> >lcs(i ->1>, j,>0>)));> >return> count;> >}> > >// Driver code> >public> static> void> main(String[] args)> >{> >int> n, m;> >X =>'abcdxyz'>;> >Y =>'xyzabcd'>;> >n = X.length();> >m = Y.length();> >System.out.println(lcs(n, m,>0>));> >}> }> // This code is contributed by Rajput-JI> |
>
>
Python3
laat gebruikers mysql zien
# Python3 program using to find length of> # the longest common substring recursion> # Returns length of function for longest> # common substring of X[0..m-1] and Y[0..n-1]> def> lcs(i, j, count):> >if> (i>=>=> 0> or> j>=>=> 0>):> >return> count> >if> (X[i>-> 1>]>=>=> Y[j>-> 1>]):> >count>=> lcs(i>-> 1>, j>-> 1>, count>+> 1>)> >count>=> max>(count,>max>(lcs(i, j>-> 1>,>0>),> >lcs(i>-> 1>, j,>0>)))> >return> count> # Driver code> if> __name__>=>=> '__main__'>:> >X>=> 'abcdxyz'> >Y>=> 'xyzabcd'> >n>=> len>(X)> >m>=> len>(Y)> >print>(lcs(n, m,>0>))> # This code is contributed by Ryuga> |
>
>
C#
// C# program using to find length> // of the longest common substring> // recursion> using> System;> class> GFG {> >static> String X, Y;> >// Returns length of function for> >// longest common substring of> >// X[0..m-1] and Y[0..n-1]> >static> int> lcs(>int> i,>int> j,>int> count)> >{> >if> (i == 0 || j == 0) {> >return> count;> >}> >if> (X[i - 1] == Y[j - 1]) {> >count = lcs(i - 1, j - 1, count + 1);> >}> >count = Math.Max(count, Math.Max(lcs(i, j - 1, 0),> >lcs(i - 1, j, 0)));> >return> count;> >}> >// Driver code> >public> static> void> Main()> >{> >int> n, m;> >X =>'abcdxyz'>;> >Y =>'xyzabcd'>;> >n = X.Length;> >m = Y.Length;> >Console.Write(lcs(n, m, 0));> >}> }> // This code is contributed by Rajput-JI> |
>
>
Javascript
> >// Javascript program using to find length of the> >// longest common substring recursion> >let X, Y;> > >// Returns length of function f> >// or longest common substring> >// of X[0..m-1] and Y[0..n-1]> >function> lcs(i, j, count)> >{> > >if> (i == 0 || j == 0)> >return> count;> > >if> (X[i - 1] == Y[j - 1]) {> >count = lcs(i - 1, j - 1, count + 1);> >}> >count = Math.max(count,> >Math.max(lcs(i, j - 1, 0),> >lcs(i - 1, j, 0)));> >return> count;> >}> > >let n, m;> > >X =>'abcdxyz'>;> >Y =>'xyzabcd'>;> > >n = X.length;> >m = Y.length;> > >document.write(lcs(n, m, 0));> > >// This code is contributed by divyeshrabadiya07.> > |
>
>
PHP
// PHP program using to find length of the // longest common substring recursion // Returns length of function for // longest common substring of // X[0..m-1] and Y[0..n-1] function lcs($i, $j, $count, &$X, &$Y) { if ($i == 0 || $j == 0) return $count; if ($X[$i - 1] == $Y[$j - 1]) { $count = lcs($i - 1, $j - 1, $count + 1, $X, $Y); } $count = max($count, lcs($i, $j - 1, 0, $X, $Y), lcs($i - 1, $j, 0, $X, $Y)); return $count; } // Driver code $X = 'abcdxyz'; $Y = 'xyzabcd'; $n = strlen($X); $m = strlen($Y); echo lcs($n, $m, 0, $X, $Y); // This code is contributed // by rathbhupendra ?>> |
>
>Uitvoer
4>
Tijdcomplexiteit : O(2^max(m,n)) aangezien de functie twee recursieve aanroepen doet – lcs(i, j-1, 0) en lcs(i-1, j, 0) wanneer karakters op X[i-1] != Y[j-1]. Het geeft dus een tijdscomplexiteit in het slechtste geval als 2^N, waarbij N = max(m, n), m en n de lengte is van de X- en Y-reeks.
Hulpruimte: O(1): omdat de functieaanroep geen extra ruimte gebruikt (de functie gebruikt alleen een recursieve aanroepstapel die we over het algemeen niet in de hulpruimte beschouwen).
