Lineaire regressie en logistieke regressie zijn de twee beroemde machine learning-algoritmen die onder toezicht vallen. Omdat beide algoritmen een gecontroleerd karakter hebben, gebruiken deze algoritmen een gelabelde dataset om de voorspellingen te doen. Maar het belangrijkste verschil tussen beide is de manier waarop ze worden gebruikt. De lineaire regressie wordt gebruikt voor het oplossen van regressieproblemen, terwijl logistieke regressie wordt gebruikt voor het oplossen van classificatieproblemen. De beschrijving van beide algoritmen wordt hieronder gegeven, samen met de verschiltabel.
Lineaire regressie:
- Lineaire regressie is een van de meest eenvoudige machine learning-algoritmen die onder de Supervised Learning-techniek valt en wordt gebruikt voor het oplossen van regressieproblemen.
- Het wordt gebruikt voor het voorspellen van de continu afhankelijke variabele met behulp van onafhankelijke variabelen.
- Het doel van de lineaire regressie is het vinden van de best passende lijn die de output voor de continu afhankelijke variabele nauwkeurig kan voorspellen.
- Als er een enkele onafhankelijke variabele wordt gebruikt voor voorspellingen, wordt dit eenvoudige lineaire regressie genoemd en als er meer dan twee onafhankelijke variabelen zijn, wordt een dergelijke regressie meervoudige lineaire regressie genoemd.
- Door de best passende lijn te vinden, legt het algoritme de relatie vast tussen de afhankelijke variabele en de onafhankelijke variabele. En de relatie moet lineair van aard zijn.
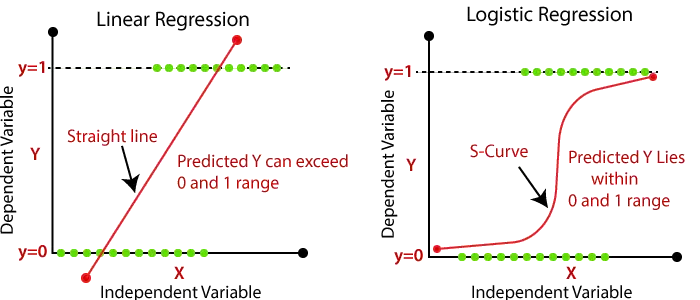
- De uitvoer voor lineaire regressie mag alleen de continue waarden zijn, zoals prijs, leeftijd, salaris, enz. De relatie tussen de afhankelijke variabele en de onafhankelijke variabele kan in onderstaande afbeelding worden weergegeven:

In bovenstaande afbeelding staat de afhankelijke variabele op de Y-as (salaris) en de onafhankelijke variabele op de x-as (ervaring). De regressielijn kan worden geschreven als:
y= a<sub>0</sub>+a<sub>1</sub>x+ ε
Waar een0en een1zijn de coëfficiënten en ε is de foutterm.
Logistieke regressie:
- Logistieke regressie is een van de meest populaire Machine Learning-algoritmen die onder Supervised Learning-technieken vallen.
- Het kan worden gebruikt voor classificatie- en regressieproblemen, maar wordt vooral gebruikt voor classificatieproblemen.
- Logistische regressie wordt gebruikt om de categorisch afhankelijke variabele te voorspellen met behulp van onafhankelijke variabelen.
- De uitvoer van het logistieke regressieprobleem kan alleen tussen 0 en 1 liggen.
- Logistieke regressie kan worden gebruikt wanneer de kansen tussen twee klassen vereist zijn. Zoals of het vandaag gaat regenen of niet, 0 of 1, waar of niet waar enz.
- Logistieke regressie is gebaseerd op het concept van maximale waarschijnlijkheidsschatting. Volgens deze schatting zouden de waargenomen gegevens het meest waarschijnlijk moeten zijn.
- Bij logistieke regressie geven we de gewogen som van de invoer door via een activeringsfunctie die waarden tussen 0 en 1 in kaart kan brengen. Een dergelijke activeringsfunctie staat bekend als sigmoïde functie en de verkregen curve wordt sigmoïde curve of S-curve genoemd. Beschouw de onderstaande afbeelding:

- De vergelijking voor logistische regressie is:

Verschil tussen lineaire regressie en logistieke regressie:
| Lineaire regressie | Logistieke regressie |
|---|---|
| Lineaire regressie wordt gebruikt om de continu afhankelijke variabele te voorspellen met behulp van een gegeven reeks onafhankelijke variabelen. | Logistische regressie wordt gebruikt om de categorisch afhankelijke variabele te voorspellen met behulp van een gegeven reeks onafhankelijke variabelen. |
| Lineaire regressie wordt gebruikt voor het oplossen van regressieproblemen. | Logistieke regressie wordt gebruikt voor het oplossen van classificatieproblemen. |
| Bij lineaire regressie voorspellen we de waarde van continue variabelen. | Bij logistieke regressie voorspellen we de waarden van categorische variabelen. |
| Bij lineaire regressie vinden we de best passende lijn, waarmee we de output gemakkelijk kunnen voorspellen. | Bij logistieke regressie vinden we de S-curve waarmee we de monsters kunnen classificeren. |
| Voor het schatten van de nauwkeurigheid wordt de kleinste kwadratenschattingsmethode gebruikt. | Voor het schatten van de nauwkeurigheid wordt de maximale waarschijnlijkheidsschattingsmethode gebruikt. |
| De uitvoer voor lineaire regressie moet een continue waarde zijn, zoals prijs, leeftijd, enz. | De uitvoer van logistieke regressie moet een categorische waarde zijn, zoals 0 of 1, Ja of Nee, enz. |
| Bij lineaire regressie is het vereist dat de relatie tussen de afhankelijke variabele en de onafhankelijke variabele lineair is. | Bij logistieke regressie is het niet vereist om de lineaire relatie tussen de afhankelijke en onafhankelijke variabele te hebben. |
| Bij lineaire regressie kan er sprake zijn van collineariteit tussen de onafhankelijke variabelen. | Bij logistische regressie mag er geen collineariteit zijn tussen de onafhankelijke variabele. |
