Lineair programmeren is een wiskundig concept dat wordt gebruikt om de optimale oplossing van de lineaire functie te vinden. Deze methode maakt gebruik van eenvoudige aannames voor het optimaliseren van de gegeven functie. Lineair Programmeren heeft een enorme toepassing in de echte wereld en wordt gebruikt om verschillende soorten problemen op te lossen.
Lineaire programmering wordt gebruikt in verschillende industrieën, zoals de scheepvaartindustrie, productie-industrie, transportindustrie, telecommunicatie en andere.
De term lineair programmeren bestaat uit twee woorden lineair en programmeren, het woord lineair vertelt de relatie tussen verschillende soorten variabelen van graad één die in een probleem worden gebruikt en het woord programmeren vertelt ons de stapsgewijze procedure om deze problemen op te lossen.
In dit artikel zullen we in detail leren over lineaire programmering, de voorbeelden, formules en andere concepten.
Inhoudsopgave
- Wat is lineaire programmering?
- Componenten van lineaire programmering
- Lineaire programmeervoorbeelden
- Lineaire programmeerproblemen
- Soorten lineaire programmeerproblemen
- Lineaire programmeerformule
- Hoe lineaire programmeerproblemen op te lossen?
- Lineaire programmeermethoden
- Lineaire programmering Simplex-methode
- Lineaire programmering grafische methode
- Lineaire programmeertoepassingen
- Belang van lineaire programmering
- Up-to-date toepassingen van lineaire programmering
- Lineaire programmering in operationeel onderzoek
- Simplex-methode
Wat is lineaire programmering?
Lineair programmeren of Lineaire optimalisatie is een techniek die ons helpt de optimale oplossing voor een bepaald probleem te vinden; een optimale oplossing is een oplossing die de best mogelijke uitkomst is van een bepaald specifiek probleem.
Simpel gezegd is het de methode om erachter te komen hoe je iets op de best mogelijke manier kunt doen. Met beperkte middelen moet u de middelen optimaal benutten en het best mogelijke resultaat behalen voor een bepaald doel, zoals de laagste kosten, de hoogste marge of de minste tijd.
De situatie die een zoektocht vereist naar de beste waarden van de variabelen die aan bepaalde beperkingen onderhevig zijn, is waar we lineaire programmeerproblemen gebruiken. Deze situaties kunnen niet worden aangepakt met de gebruikelijke calculus- en numerieke technieken.
Lineaire programmeringsdefinitie
Lineaire programmering is de techniek die wordt gebruikt voor het optimaliseren van een bepaald scenario. Het gebruik van lineaire programmering biedt ons de best mogelijke uitkomst in een bepaalde situatie. Het zet alle beschikbare middelen zo in dat ze het optimale resultaat opleveren.
Componenten van lineaire programmering
De basiscomponenten van een lineair programmeerprobleem (LP) zijn:
- Beslissingsvariabelen: Variabelen die u wilt bepalen om de optimale oplossing te bereiken.
- Doelfunctie: M athematische vergelijking die het doel vertegenwoordigt dat u wilt bereiken
- Beperkingen: Beperkingen of beperkingen waaraan uw beslissingsvariabelen moeten voldoen.
- Niet-negativiteitsbeperkingen: In bepaalde In praktijkscenario's kunnen beslissingsvariabelen niet negatief zijn
Aanvullende kenmerken van lineaire programmering
- Eindigheid: Het aantal beslissingsvariabelen en beperkingen in een LP-probleem is eindig.
- Lineariteit: De objectieve functie en alle beperkingen moeten lineaire functies zijn van de beslissingsvariabelen . Het betekent dat het aantal variabelen één moet zijn.
Lineaire programmeervoorbeelden
We kunnen de situaties begrijpen waarin lineaire programmering wordt toegepast met behulp van het hieronder besproken voorbeeld:
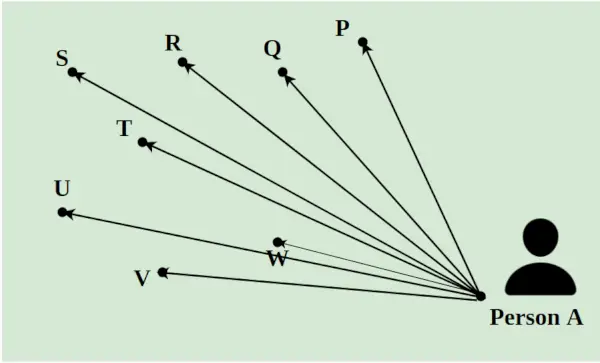
Stel dat een bezorger op een dag 8 pakketten moet bezorgen op verschillende locaties in een stad. Hij moet alle pakketten van A kiezen en ze afleveren bij de punten P, Q, R, S, T, U, V en W. De afstand ertussen wordt aangegeven met behulp van de lijnen zoals weergegeven in de onderstaande afbeelding. Het kortste pad dat de bezorger volgt, wordt berekend met behulp van het concept van lineaire programmering.
preity zinta
Lineaire programmeerproblemen
Lineaire programmeerproblemen (LPP) omvatten het optimaliseren van een lineaire functie om de optimale waardeoplossing voor de functie te vinden. De optimale waarde kan de maximale waarde of de minimale waarde zijn.
In LPP worden de lineaire functies aangeroepen objectieve functies. Een objectieve functie kan meerdere variabelen hebben, die aan voorwaarden onderworpen zijn en aan de voorwaarden moeten voldoen lineaire beperkingen .
Soorten lineaire programmeerproblemen
Er zijn veel verschillende lineaire programmeerproblemen (LPP), maar we zullen in dit artikel drie belangrijke lineaire programmeerproblemen behandelen.
Productieproblemen
Productieproblemen zijn een probleem dat te maken heeft met het aantal eenheden dat geproduceerd of verkocht moet worden om de winst te maximaliseren, wanneer elk product vaste mankracht, machine-uren en grondstoffen vereist.
Dieetproblemen
Het wordt gebruikt om het aantal verschillende soorten bestanddelen te berekenen dat in het dieet moet worden opgenomen om de minimale kosten te verkrijgen, afhankelijk van de beschikbaarheid van voedsel en de prijzen ervan.
Transportproblemen
Het wordt gebruikt om het transportschema te bepalen om de goedkoopste manier te vinden om een product te transporteren van fabrieken/fabrieken op verschillende locaties naar verschillende markten.
Lineaire programmeerformule
Een lineair programmeerprobleem bestaat uit:
- Beslissingsvariabelen
- Objectieve functie
- Beperkingen
- Niet-negatieve beperkingen
Beslissingsvariabelen zijn de variabelen x en y, die de uitkomst van het lineaire programmeerprobleem bepalen en de uiteindelijke oplossing vertegenwoordigen.
De objectieve functie , doorgaans weergegeven door Z, is de lineaire functie die moet worden geoptimaliseerd volgens de gegeven voorwaarde om de uiteindelijke oplossing te krijgen.
De beperkingen opgelegd aan beslissingsvariabelen die hun waarden beperken, worden beperkingen genoemd.
De algemene formule van een lineair programmeerprobleem is:
Objectieve functie : Z = bijl + door
Beperkingen: cx + dy ≥ e, px + qy ≤ r
Niet-negatieve beperkingen: x ≥ 0, y ≥ 0
In de bovenstaande voorwaarde zijn x en y de beslissingsvariabelen.
Hoe lineaire programmeerproblemen op te lossen?
Voordat we de lineaire programmeerproblemen oplossen, moeten we eerst de problemen formuleren volgens de standaardparameters. De stappen voor het oplossen van lineaire programmeerproblemen zijn:
Stap 1: Markeer de beslissingsvariabelen in het probleem.
Stap 2: Bouw de objectieve functie van het probleem en controleer of de functie geminimaliseerd of gemaximaliseerd moet worden.
Stap 3: Schrijf alle beperkingen van de lineaire problemen op.
Stap 4: Zorg voor niet-negatieve beperkingen van de beslissingsvariabelen.
Stap 5: Los nu het lineaire programmeerprobleem op met behulp van een willekeurige methode. Over het algemeen gebruiken we de simplex- of grafische methode.
Lineaire programmeermethoden
We gebruiken verschillende methoden voor het oplossen van lineaire programmeerproblemen. De twee meest gebruikte methoden zijn:
- Simplex-methode
- Grafische methode
Laten we deze twee methoden in detail leren kennen in dit artikel,
Lineaire programmering Simplex-methode
Een van de meest gebruikelijke methoden om het lineaire programmeerprobleem op te lossen is de simplexmethode. Bij deze methode herhalen we een specifieke voorwaarde ‘n’ een aantal keren totdat een optimale oplossing is bereikt.
De stappen die nodig zijn om lineaire programmeerproblemen op te lossen met behulp van de simplexmethode zijn:
Stap 1: Formuleer de lineaire programmeerproblemen op basis van de gegeven beperkingen.
Stap 2: Converteer alle gegeven ongelijkheden naar vergelijkingen of gelijkheden van de lineaire programmeerproblemen door de slack-variabele aan elke ongelijkheid toe te voegen waar dat ooit nodig is.
Stap 3: Construeer de initiële simplextabel. Door elke beperkingsvergelijking in een rij weer te geven en de doelfunctie in de onderste rij te schrijven. De aldus verkregen tabel wordt de Simplex-tabel genoemd.
Stap 4: Identificeer de grootste negatieve waarde in de onderste rij. De kolom van het element met de hoogste negatieve waarde wordt de draaitabel genoemd
Stap 5: Verdeel de vermeldingen van de meest rechtse kolom met de vermeldingen van de betreffende draaikolom, met uitzondering van de vermeldingen van de onderste rij. Nu wordt de rij met de minste invoer de draairij genoemd. Het scharnierelement wordt verkregen door het snijpunt van de scharnierrij en de scharnierkolom.
Stap 6: Maak met behulp van matrixbewerkingen en met behulp van het draaielement alle vermeldingen in de draaikolom nul.
Stap 7: Controleer of er niet-negatieve vermeldingen in de onderste rij staan. Als er geen negatieve vermeldingen in de onderste rij staan, beëindig dan het proces, start anders het proces opnieuw vanaf stap 4.
Stap 8: De aldus verkregen uiteindelijke simplextabel geeft de oplossing voor ons probleem.
Lineaire programmering grafische methode
Grafische methode is een andere methode dan de Simplex-methode die wordt gebruikt om lineaire programmeerproblemen op te lossen. Zoals de naam al doet vermoeden, gebruikt deze methode grafieken om de gegeven lineaire programmeerproblemen op te lossen. Dit is de beste methode om lineaire programmeerproblemen op te lossen en vereist minder inspanning dan de simplexmethode.
Terwijl we deze methode gebruiken, brengen we alle ongelijkheden in kaart die onderhevig zijn aan beperkingen in de gegeven lineaire programmeerproblemen. Zodra alle ongelijkheden van de gegeven LPP in de XY-grafiek zijn uitgezet, geeft het gemeenschappelijke gebied van alle ongelijkheden de optimale oplossing. Alle hoekpunten van het haalbare gebied worden berekend en de waarde van de objectieve functie op al die punten wordt berekend. Door deze waarden te vergelijken, krijgen we de optimale oplossing van de LPP.
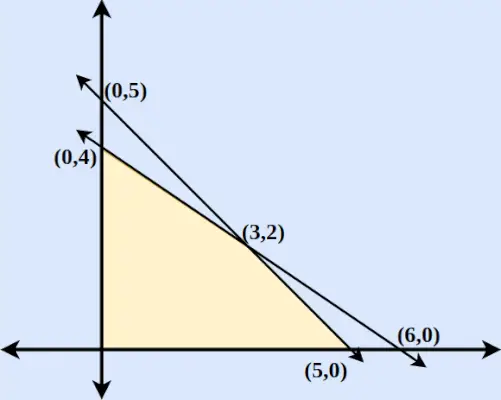
Voorbeeld: Vind de maximale en minimale waarde van z = 6x + 9y wanneer de beperkingsvoorwaarden zijn:
- 2x + 3j ≤ 12
- x en y ≥ 0
- x + y ≤ 5
Oplossing:
Stap 1 : Zet eerst de ongelijkheden om in normale vergelijkingen. De vergelijkingen zijn dus 2x+3y = 0, x = 0, y = 0 en x + y = 5.
Stap 2 : Zoek de punten waarop 2x + 3y en x + y = 5 de x-as en y-as snijden. Om het snijpunt van de x-as te vinden, plaatst u y = 0 in de betreffende vergelijking en zoekt u het punt. Op dezelfde manier plaatst u voor de snijpunten van de y-as x = 0 in de betreffende vergelijking.
Stap 3 : Teken de twee lijnen die de x-as en de y-as doorsnijden. We zien dat de twee assen elkaar snijden bij (3,2).
Stap 4 : Voor x ≥ 0 en y ≥ 0 vinden we dat beide ongelijkheden worden gevolgd. De regio omvat dus een gebied dat wordt omsloten door twee assen en waarbij beide lijnen de oorsprong omvatten. Het uitgezette gebied wordt hieronder in de figuur weergegeven.
Stap 5 : Zoek Z voor elk punt en maxima en minima.
Coördinaten Z = 6x + 9j (0,5) Z=45 (0,4) Z=36 (5,0) Z=30 (6,0) Z=36 (3.2) Z=36 We vinden dus dat Z = 6x + 9y maximaal is bij (0,5) en minimaal bij (5,0).
Lineaire programmeertoepassingen
Lineair Programmeren heeft toepassingen op verschillende gebieden. Het wordt gebruikt om de minimale kosten van een proces te vinden wanneer alle beperkingen van de problemen gegeven zijn. Het wordt gebruikt om de transportkosten van het voertuig enz. te optimaliseren. Er zijn verschillende toepassingen van lineaire programmering
Technische Industrieën
Engineering Industries gebruiken lineaire programmering om ontwerp- en productieproblemen op te lossen en om de maximale output uit een bepaalde omstandigheid te halen.
Verwerkende industrieën
Productie-industrieën gebruiken lineaire programmering om de winst van de bedrijven te maximaliseren en de productiekosten te verlagen.
Energie-industrieën
Energiebedrijven gebruiken lineaire programmering om hun productie-output te optimaliseren.
Transportindustrieën
Lineaire programmering wordt ook gebruikt in de transportsector om de weg te vinden om de transportkosten te minimaliseren.
Belang van lineaire programmering
Lineaire programmering is van groot belang in verschillende industrieën. Het maximaliseert de uitvoerwaarde en minimaliseert de invoerwaarden volgens verschillende beperkingen.
LP is zeer toepasbaar wanneer we meerdere voorwaarden hebben bij het oplossen van een probleem en we de output van het probleem moeten optimaliseren, dat wil zeggen dat we de minimale of de maximale waarde moeten vinden volgens een bepaalde voorwaarde.
Lees verder,
- Lineaire ongelijkheden
- Algebraïsche oplossing van lineaire ongelijkheden
Lineaire programmeerproblemen
Probleem 1: Een bedrijf produceert en verkoopt twee soorten producten en de productiekosten van elke eenheid a en b bedragen respectievelijk 200 en 150 roepies. Elke eenheid product levert een winst op van 20 roepies en elke eenheid product b levert een winst op van 15 roepies bij verkoop . Het bedrijf schat dat de maandelijkse vraag van A en B maximaal de geoogste eenheid bedraagt, terwijl het productiebudget voor de maand is vastgesteld op 50.000 roepies. Hoeveel eenheden moet het bedrijf produceren om maximale winst te behalen uit de maandelijkse verkoop van een en B?
Oplossing:
Stel x = aantal eenheden van type A
y = Aantal eenheden van type B
Maximaliseer Z = 40x + 50y
Onderworpen aan de beperkingen
3x + y ≤ 9
x + 2y ≤ 8
en x, y ≥ 0
Beschouw de vergelijking,
3x + y = 9
x = 3
j = 0
en x + 2y = 8
x = 8
j = 0
Nu kunnen we de maximale waarde van Z bepalen door de waarde van Z op de vier punten (hoekpunten) te evalueren, zoals hieronder weergegeven
Hoekpunten
Z = 40x + 50j
(0, 0)
Z = 40 × 0 + 50 × 0 = Rs. 0
(3, 0)
Z = 40 × 3 + 50 × 0 = Rs. 120
(0, 4)
Z = 40 × 0 + 50 × 4 = Rs. 200
(23)
Z = 40 × 2 + 50 × 3 = Rs. 230
Maximale winst, Z = Rs. 230
∴ Aantal eenheden van type A is 2 en het aantal eenheden van type B is 3.
Probleem 2: Maximaliseer Z = 3x + 4y.
Onderworpen aan beperkingen, x + y ≤ 450, 2x + y ≤ 600 en x, y ≤ 0.
Oplossing:
Wij hebben van het gegeven
Beperkingen (1)
X+Y= 450
Stel x = 0, ⇒ 0 + y = 450 ⇒ y = 450
Stel y = 0, ⇒ x + 0 = 450 ⇒ x = 450
Van, Beperkingen (2)
onveranderlijke lijst2x + y = 600
Stel x = 0, ⇒ 0 + y = 600 ⇒ y = 600
Stel y = 0, ⇒ 2x + 0 = 600 ⇒ x = 300
Nu hebben we de puntencoördinaat Z = 3x + 4y
| Hoekpunten | Z = 3x + 4j |
|---|---|
| (0, 0) | Z = 3 × 0 + 4 × 0 = 0 |
| (300, 0) | Z = 3 × 300+ 4 × 0 = 900 |
| (150, 300) | Z = 3 × 150 + 4 × 300 = 1650 |
| (0, 450) | Z = 3 × 0 + 4 × 450 = 1800 |
Daarom is het optimale oplossingsmaximum Z = 1800 bij coördinaat x = 0 en y = 450. De grafiek wordt hieronder gegeven.

Up-to-date toepassingen van lineaire programmering
Lineair programmeren, een krachtige wiskundige techniek, wordt gebruikt om optimalisatieproblemen in verschillende industrieën op te lossen. Hier zijn enkele moderne toepassingen:
- Optimalisatie van de toeleveringsketen : Lineaire programmering helpt bedrijven de kosten te minimaliseren en de efficiëntie in hun toeleveringsketens te maximaliseren. Het wordt gebruikt voor het bepalen van de meest kosteneffectieve transportroutes, magazijnactiviteiten en voorraadbeheerstrategieën.
- Energiebeheer : In de energiesector wordt lineaire programmering gebruikt om de mix van energieproductiemethoden te optimaliseren. Dit omvat het balanceren van traditionele energiebronnen met hernieuwbare energiebronnen om de kosten en de impact op het milieu te verminderen en tegelijkertijd aan de vraag te voldoen.
- Telecommunicatienetwerkontwerp : Lineaire programmeerhulpmiddelen bij het ontwerpen van efficiënte telecommunicatienetwerken. Het helpt bij het toewijzen van bandbreedte, het ontwerpen van netwerkindelingen en het optimaliseren van de gegevensstroom om snelle communicatie tegen lagere kosten te garanderen.
- Financiële planning : Bedrijven en financiële analisten gebruiken lineaire programmering voor portefeuilleoptimalisatie, risicobeheer en kapitaalbudgettering. Het helpt bij het nemen van investeringsbeslissingen die het rendement maximaliseren en tegelijkertijd het risico minimaliseren.
- Gezondheidszorg Logistiek : In de gezondheidszorg wordt lineaire programmering toegepast om de toewijzing van middelen, zoals ziekenhuisbedden, medisch personeel en apparatuur, te optimaliseren. Het is van cruciaal belang voor het verbeteren van de patiëntenzorg, het terugdringen van wachttijden en het effectief beheersen van de kosten.
- Optimalisatie van productieproces : Lineaire programmering wordt gebruikt om de optimale productieniveaus voor meerdere producten binnen een productiefaciliteit te bepalen, rekening houdend met beperkingen zoals arbeid, materialen en machinebeschikbaarheid.
- Landbouwplanning : Boeren en landbouwplanners gebruiken lineaire programmering om te beslissen over gewasselectie, landgebruik en toewijzing van hulpbronnen om de opbrengsten en winsten te maximaliseren en tegelijkertijd hulpbronnen te behouden.
- Planning van luchtvaartpersoneel : Luchtvaartmaatschappijen maken gebruik van lineaire programmering om bemanningen efficiënt in te plannen, ervoor te zorgen dat vluchten worden bemand in overeenstemming met de regelgeving en de operationele kosten tot een minimum worden beperkt.
Deze toepassingen demonstreren de veelzijdigheid en kracht van lineair programmeren bij het oplossen van complexe optimalisatieproblemen in verschillende sectoren, en tonen de relevantie ervan in de huidige datagestuurde wereld.
Lineaire programmering in operationeel onderzoek
- Kern gereedschap : Lineaire programmering is een fundamenteel hulpmiddel in operationeel onderzoek voor het optimaliseren van hulpbronnen.
- Besluitvorming : Helpt bij het nemen van de beste beslissingen met betrekking tot de toewijzing van middelen, het maximaliseren van de winst of het minimaliseren van de kosten.
- Brede toepassingen : Gebruikt op verschillende gebieden, zoals logistiek, productie, financiën en gezondheidszorg, voor het oplossen van complexe problemen.
- Modellering van problemen uit de echte wereld : Transformeert problemen uit de echte wereld in wiskundige modellen om de meest efficiënte oplossingen te vinden.
Simplex-methode
- Optimalisatie-algoritme : De Simplex-methode is een krachtig algoritme dat bij lineair programmeren wordt gebruikt om de optimale oplossing voor lineaire ongelijkheden te vinden.
- Stapsgewijze aanpak : Het beweegt iteratief naar de beste oplossing door langs de randen van het haalbare gebied te navigeren dat door beperkingen wordt gedefinieerd.
- Efficiëntie : Bekend om zijn efficiëntie bij het oplossen van grootschalige lineaire programmeerproblemen.
- Veelzijdigheid : Toepasbaar in verschillende domeinen, zoals dieetplanning, netwerkstromen, productieplanning en meer, wat de veelzijdigheid ervan aantoont.
Lineaire programmering – Veelgestelde vragen
Wat is lineaire programmering?
Lineaire programmering is een wiskundig concept dat wordt gebruikt om een bepaald lineair probleem te optimaliseren dat verschillende beperkingen kent. Met behulp van lineaire programmering kunnen we de optimale uitkomst van het gegeven probleem bereiken
Wat zijn lineaire programmeerproblemen?
Lineaire Programmeerproblemen (LPP) zijn de problemen die de optimale oplossing bieden voor de gegeven omstandigheden.
Wat is lineaire programmeerformule?
Algemene lineaire programmeerformules zijn,
- Doelfunctie: Z = bijl + door
- Beperkingen: px + qy ≤ r, sx + ty ≤ u
- Niet-negatieve beperkingen: x ≥ 0, y ≥ 0
Wat zijn de verschillende soorten lineaire programmering?
Verschillende soorten lineaire programmeermethoden zijn,
- Lineaire programmering volgens Simplex-methode
- Lineaire programmering volgens R-methode
- Lineaire programmering via grafische methode
Wat zijn de vereisten voor lineair programmeren?
Verschillende vereisten voor lineaire programmeerproblemen zijn:
- Lineariteit
- Objectieve functie
- Beperkingen
- Niet-negativiteit
Wat zijn de voordelen van lineair programmeren?
Verschillende voordelen van lineair programmeren zijn:
- Het biedt de optimale oplossing voor elk lineair probleem.
- Het is gemakkelijk te gebruiken en geeft altijd consistente resultaten
- Het helpt de winst te maximaliseren en de inputkosten te verlagen.