Gelijke termen zijn termen in algebraïsche uitdrukkingen die dezelfde variabelen hebben, verheven tot dezelfde machten. Like- en In tegenstelling-termen zijn de typen termen in de algebra, en we kunnen onderscheid maken tussen gelijke en ongelijke termen door simpelweg de variabelen en hun machten te controleren. We definiëren algebraïsche termen als de individuele termen die zijn verkregen uit de algebraïsche vergelijking.
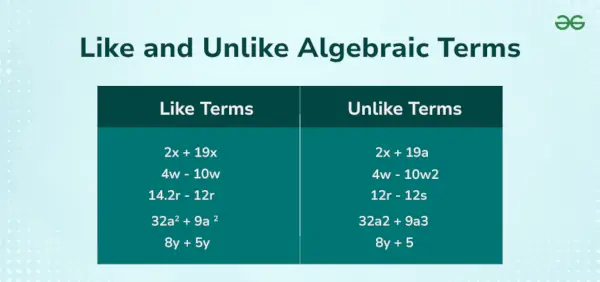
Bijvoorbeeld in de algebraïsche vergelijking 5x + 3j 2 = 12 we hebben drie termen die zijn: 5x, 3j², En 12 . Hier, 5x, En 3j 2 zijn variabele termen en 12 is de constante term. De onderstaande afbeelding toont de termen 'gelijk' en 'niet leuk'.
In dit artikel zullen we in detail leren over soortgelijke termen, anders-termen, hun voorbeelden, vereenvoudiging en andere.
Zoals termen
Gelijkaardige termen zijn de termen die dezelfde variabelen hebben en de kracht van elk van de variabelen is ook hetzelfde. We kunnen soortgelijke termen combineren om de algebraïsche uitdrukkingen te vereenvoudigen, en dit kan heel eenvoudig worden berekend. 3y + 5y is bijvoorbeeld een algebraïsche uitdrukking met soortgelijke termen 3y en 5y. Om deze algebraïsche uitdrukking te vereenvoudigen, voegen we soortgelijke termen toe. De vereenvoudiging van de gegeven uitdrukking is dus 8y.
Voorbeelden van soortgelijke termen
Gelijksoortige termen zijn de termen die dezelfde variabele hebben met een vergelijkbare kracht. Enkele voorbeelden van soortgelijke termen zijn:
- 40xy 2 en 56xy 2 : In het eerste voorbeeld xy2is de gemeenschappelijke coëfficiënt voor beide termen. Het zijn dus net termen.
- 30z 2 en 18z 2 : Met2is de gemeenschappelijke coëfficiënt voor beide termen. Het zijn dus net termen.
- 45abc en 29abc: abc is de gemeenschappelijke coëfficiënt voor beide termen. Het zijn dus net termen.
- 18r 3 en 38r 3 : R3is de gemeenschappelijke coëfficiënt voor beide termen. Het zijn dus net termen.
- 2xy en 8xy: xy is de gemeenschappelijke coëfficiënt voor beide termen. Het zijn dus net termen.
Optellen en aftrekken van soortgelijke termen
We kunnen gemakkelijk soortgelijke termen optellen en aftrekken en er zijn geen speciale regels voor nodig. Ze worden over het algemeen vereenvoudigd met behulp van de normale regels voor optellen en aftrekken. We kunnen dit concept begrijpen aan de hand van het volgende voorbeeld.
Voorbeeld: Vereenvoudig 11x 3 + 5x 3
java elseif
Oplossing:
Zoals we zien, zijn dit soortgelijke termen omdat ze vergelijkbare variabelen hebben en hun kracht ook constant is.
Deze termen kunnen wij eenvoudig direct toevoegen.
= 11x3+ 5x3
= 16x3
Dit is mogelijk omdat ze dezelfde variabelen hebben met een vergelijkbare kracht en dit kan worden begrepen als: we kunnen rechtstreeks roepies bij roepies optellen, d.w.z. 5 Rs + 7 Rs is 12 Rs. Maar we kunnen niet direct roepies toevoegen aan dollars en 5 Rs + 7 dollar kunnen niet direct worden vereenvoudigd.
java-tekenreeks naar geheel getal
Op dezelfde manier kunnen we soortgelijke termen ook rechtstreeks aftrekken. Voeg gewoon gelijke termen toe, dit kan worden begrepen aan de hand van het volgende voorbeeld.
Voorbeeld 1: Vereenvoudig 11x 3 – 5x 3
Oplossing:
Zoals we zien, zijn dit soortgelijke termen omdat ze vergelijkbare variabelen hebben en hun kracht ook constant is.
We kunnen deze termen gemakkelijk rechtstreeks aftrekken.
= 11x3– 5x3
= 6x3
Voorbeeld 2: Voeg 3 toe X + 2 En + 5 en 4 X − 3 En + 7.
Oplossing:
(3 X + 2 En + 5) + (4 X − 3 En + 7)
= (3 X + 4x) +(2j + (-3j))+ (5 + 7)
= 7 X − En + 12
In tegenstelling tot voorwaarden
In tegenstelling tot termen zijn termen met verschillende variabelen en elk van de variabelen kan al dan niet verschillende exponenten hebben. 9x + 6y is bijvoorbeeld een algebraïsche uitdrukking met afwijkende termen. Omdat het twee verschillende variabelen x en y heeft.
Als de variabelen verschillend zijn, controleren we de macht niet, omdat ze op enigerlei wijze verschillen van termen, maar als de variabelen hetzelfde zijn, controleren we op hun macht, omdat ze wel of niet op termen lijken.
Zoals 5x2en 6x2zijn als termen, maar 5x2en 6x3zijn anders dan termen.
Voorbeelden van tegenstellingsvoorwaarden
In tegenstelling tot termen zijn het de termen die niet dezelfde variabelen of vergelijkbare kracht hebben. Enkele voorbeelden van ongelijke termen zijn:
- 40xy 2 en 56xy: Hier is in één algebraïsche uitdrukking de variabele xy2en in de andere algebraïsche uitdrukking is de variabele xy. Beide variabelen zijn hetzelfde, maar hebben verschillende bevoegdheden. Ze zijn dus anders dan termen.
- 45abc en 29ab: Hier is in de ene algebraïsche uitdrukking de variabele abc en in de andere algebraïsche uitdrukking de variabele ab. Beide variabelen zijn verschillend. Ze vallen dus in de categorie van, in tegenstelling tot termen.
Optellen en aftrekken van ongelijke termen
Optellen en aftrekken wordt niet uitgevoerd tussen ongelijke termen, d.w.z. we kunnen geen ongelijke termen optellen of aftrekken. Dit kan aan de hand van het voorbeeld worden begrepen, aangezien we geen 5 liter melk kunnen toevoegen aan 6 kg rijst. Op dezelfde manier kunnen we, in tegenstelling tot termen, niet optellen of aftrekken.
3xy + 5x kan bijvoorbeeld niet verder worden opgelost en blijft op dezelfde manier staan.
Verschil tussen soortgelijke termen en in tegenstelling tot termen
De verschillen tussen soortgelijke termen en niet-gelijksoortige termen worden in de onderstaande tabel besproken.
| Functie hernoem de Linux-map | Zoals termen | In tegenstelling tot voorwaarden |
|---|---|---|
| Definitie | Gelijksoortige termen zijn de termen die dezelfde variabelen hebben en dezelfde exponentwaarden. | In tegenstelling tot termen zijn termen die verschillende variabelen hebben en exponenten. |
| Vereenvoudiging | We kunnen soortgelijke termen gemakkelijk vereenvoudigen. | In tegenstelling tot termen die niet vereenvoudigd kunnen worden. |
| Termen combineren | Gelijke termen kunnen direct worden gecombineerd om berekeningen te maken. | In tegenstelling tot termen kunnen ze niet rechtstreeks worden gecombineerd omdat ze verschillende grootheden vertegenwoordigen |
| Optellen of aftrekken | Optellen en aftrekken kan in dezelfde termen worden bereikt. | In tegenstelling tot termen kunnen we niet optellen of aftrekken. |
| Voorbeelden | Voorbeelden van soortgelijke termen zijn x2, 5x2, -11/3x2, enz. | Voorbeelden van tegenstelling-termen zijn x2en, 5x3, -11/3x, enz. |
Lees verder
- Algebraïsche uitdrukkingen
- Soorten algebraïsche uitdrukkingen
Voorbeelden van algebraïsche termen zoals en niet-gelijk
Voorbeeld 1: Identificeer gelijke en ongelijke termen uit: 3x, 5xy, 18x 2 en, 5x 3 , 29xy, 50x 3
java boolean naar string
Oplossing:
Like en In tegenstelling tot termen uit de gegeven termen zijn:
Vind ik leuk voorwaarden: (5xy, 29xy) en (5x3, 50x3)
In tegenstelling tot termen: 3x, 18x2En
Voorbeeld 2: Vereenvoudig 3xy + 5x 2 + 11ab – 4xy
Oplossing:
Gegeven uitdrukking: 3xy + 5x2+ 11ab – 4xy
Zoals de term in de gegeven uitdrukking, 3xy en -4xy
Over vereenvoudigen,
= 3xy – 4xy + 5x2+ 11ab
= -xy + 5x2+ 11ab
Rest: alle termen zijn verschillend van termen, dus ze kunnen niet verder worden opgelost.
Voorbeeld 3: Vereenvoudig 8x + 15x 2 + 11x – 4x 2
Oplossing:
Gegeven uitdrukking: 8x + 15x2+ 11x – 4x2
Zoals de term in de gegeven uitdrukking, (8x, 11x) en (15x2, -4x2)
Over vereenvoudigen,
= 8x + 11x + 15x2– 4x2
rhel versus centos= 19x – 11x2
Rest: alle termen zijn verschillend van termen, dus ze kunnen niet verder worden opgelost.
Vind ik leuk en in tegenstelling tot algebraïsche termen – Veelgestelde vragen
Wat zijn algebraïsche termen?
Algebraïsche termen zijn de individuele termen die zijn verkregen uit de algebraïsche vergelijking, dat wil zeggen termen gedeeld door de bewerkingssymbolen zoals + en -.
Wat zijn 'like'- en 'in tegenstelling'-termen?
Gelijksoortige en ongelijksoortige termen zijn de termen van de algebraïsche uitdrukking. In vergelijkbare termen hebben we vergelijkbare variabelen en is de macht van de exponent hetzelfde, terwijl in ongelijke termen de variabelen en hun macht anders zijn.
Wat is het verschil tussen algebraïsche termen zoals en niet?
Het fundamentele verschil tussen gelijke en ongelijke termen is dat we in de gelijke term dezelfde variabele met dezelfde machten hebben, terwijl we in ongelijke termen verschillende variabelen met verschillende machten hebben.
Hoe vind ik de algebraïsche termen 'Like' en 'In tegenstelling'?
Gelijksoortige termen zijn de termen die dezelfde variabelen hebben met dezelfde machten en de ongelijke termen zijn de termen met verschillende variabelen en verschillende machten. We kunnen ze gemakkelijk identificeren door simpelweg de variabelen te inspecteren.
Kunnen we optellen of aftrekken zoals algebraïsche termen?
We kunnen gemakkelijk soortgelijke termen optellen of aftrekken, zoals 5x en 11x, zijn soortgelijke termen en ze kunnen worden opgeteld als 16x.
Kunnen we optellen of aftrekken in tegenstelling tot algebraïsche termen?
We kunnen niet optellen of aftrekken in tegenstelling tot termen als 2x en 3y. Anderstalige termen kunnen dus niet bij elkaar worden opgeteld of afgetrokken.
