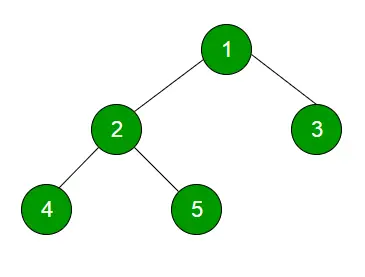
Traversatie van niveauorders techniek wordt gedefinieerd als een methode om een Boom zodanig te doorkruisen dat alle knooppunten op hetzelfde niveau volledig worden doorlopen voordat ze naar het volgende niveau gaan.

Voorbeeld:
Aanbevolen oefenniveau voor het doorlopen van orders Probeer het!Invoer:
Uitgang:
1
23
Vier vijf
Hoe werkt Level Order Traversal?
Het belangrijkste idee van level order traversal is om alle knooppunten van een lager niveau te doorlopen voordat je naar een van de knooppunten van een hoger niveau gaat. Dit kan op een van de volgende manieren:
- de naïeve (de hoogte van de boom vinden en elk niveau doorkruisen en de knooppunten van dat niveau afdrukken)
- efficiënt gebruik van een wachtrij.
Level Order Traversal (naïeve benadering):
Vinden hoogte van boom. Voer vervolgens voor elk niveau een recursieve functie uit door de huidige hoogte te behouden. Wanneer het niveau van een knooppunt overeenkomt, drukt u dat knooppunt af.
Hieronder vindt u de implementatie van de bovenstaande aanpak:
C++ // Recursive CPP program for level // order traversal of Binary Tree #include using namespace std; // A binary tree node has data, // pointer to left child // and a pointer to right child class node { public: int data; node *left, *right; }; // Function prototypes void printCurrentLevel(node* root, int level); int height(node* node); node* newNode(int data); // Function to print level order traversal a tree void printLevelOrder(node* root) { int h = height(root); int i; for (i = 1; i <= h; i++) printCurrentLevel(root, i); } // Print nodes at a current level void printCurrentLevel(node* root, int level) { if (root == NULL) return; if (level == 1) cout << root->gegevens<< ' '; else if (level>1) { printCurrentLevel(root->links, niveau - 1); printCurrentLevel(root->rechts, niveau - 1); } } // Bereken de 'hoogte' van een boom -- het aantal // knooppunten langs het langste pad vanaf het hoofdknooppunt // tot aan het verste bladknooppunt. int hoogte(knooppunt* knooppunt) { if (knooppunt == NULL) return 0; else {// Bereken de hoogte van elke subboom int lheight = height(node->left); int rheight = hoogte(knooppunt->rechts); // Gebruik de grotere if (lheight> rheight) { return (lheight + 1); } anders { return (hoogte + 1); } } } // Helperfunctie die // een nieuw knooppunt toewijst met de gegeven gegevens en // NULL linker- en rechteraanwijzers. knooppunt* newNode(int-gegevens) { knooppunt* Knooppunt = nieuw knooppunt(); Knooppunt->gegevens = gegevens; Knooppunt->links = NULL; Knooppunt->rechts = NULL; terugkeer (knooppunt); } // Stuurprogrammacode int main() { node* root = newNode(1); root->links = newNode(2); root->right = newNode(3); root->links->links = newNode(4); root->links->rechts = newNode(5); uit<< 'Level Order traversal of binary tree is
'; printLevelOrder(root); return 0; } // This code is contributed by rathbhupendra> C // Recursive C program for level // order traversal of Binary Tree #include #include // A binary tree node has data, // pointer to left child // and a pointer to right child struct node { int data; struct node *left, *right; }; // Function prototypes void printCurrentLevel(struct node* root, int level); int height(struct node* node); struct node* newNode(int data); // Function to print level order traversal a tree void printLevelOrder(struct node* root) { int h = height(root); int i; for (i = 1; i <= h; i++) printCurrentLevel(root, i); } // Print nodes at a current level void printCurrentLevel(struct node* root, int level) { if (root == NULL) return; if (level == 1) printf('%d ', root->gegevens); else if (niveau> 1) { printCurrentLevel(root->left, level - 1); printCurrentLevel(root->rechts, niveau - 1); } } // Bereken de 'hoogte' van een boom -- het aantal // knooppunten langs het langste pad vanaf het hoofdknooppunt // tot aan het verste bladknooppunt int height(struct node* node) { if (node == NULL) retourneert 0; else {// Bereken de hoogte van elke subboom int lheight = height(node->left); int rheight = hoogte(knooppunt->rechts); // Gebruik de grotere als (lheight> rheight) retourneert (lheight + 1); anders retour (rechts + 1); } } // Helperfunctie die een nieuw knooppunt toewijst met de // gegeven gegevens en NULL linker- en rechteraanwijzers. struct node* newNode(int data) { struct node* node = (struct node*)malloc(sizeof(struct node)); knooppunt->gegevens = gegevens; knooppunt->links = NULL; knooppunt->rechts = NULL; terugkeer (knooppunt); } // Stuurprogramma om bovenstaande functies te testen int main() { struct node* root = newNode(1); root->links = newNode(2); root->right = newNode(3); root->links->links = newNode(4); root->links->rechts = newNode(5); printf('Niveauvolgorde door de binaire boom is
'); printLevelOrder(root); retour 0; }> Java // Recursive Java program for level // order traversal of Binary Tree // Class containing left and right child of current // node and key value class Node { int data; Node left, right; public Node(int item) { data = item; left = right = null; } } class BinaryTree { // Root of the Binary Tree Node root; public BinaryTree() { root = null; } // Function to print level order traversal of tree void printLevelOrder() { int h = height(root); int i; for (i = 1; i <= h; i++) printCurrentLevel(root, i); } // Compute the 'height' of a tree -- the number of // nodes along the longest path from the root node // down to the farthest leaf node. int height(Node root) { if (root == null) return 0; else { // Compute height of each subtree int lheight = height(root.left); int rheight = height(root.right); // use the larger one if (lheight>hoogte) retour (lhoogte + 1); anders retour (rechts + 1); } } // Print knooppunten op het huidige niveau void printCurrentLevel(Node root, int level) { if (root == null) return; if (niveau == 1) System.out.print(root.data + ' '); else if (niveau> 1) { printCurrentLevel(root.left, niveau - 1); printCurrentLevel(root.right, niveau - 1); } } // Stuurprogramma om bovenstaande functies te testen public static void main(String args[]) { BinaryTree tree = new BinaryTree(); tree.root = nieuw knooppunt (1); tree.root.left = nieuw knooppunt(2); tree.root.right = nieuw knooppunt(3); tree.root.left.left = nieuw knooppunt(4); tree.root.left.right = nieuw knooppunt(5); System.out.println('Niveauvolgorde doorlopen van' + 'binaire boom is '); boom.printLevelOrder(); } }> Python # Recursive Python program for level # order traversal of Binary Tree # A node structure class Node: # A utility function to create a new node def __init__(self, key): self.data = key self.left = None self.right = None # Function to print level order traversal of tree def printLevelOrder(root): h = height(root) for i in range(1, h+1): printCurrentLevel(root, i) # Print nodes at a current level def printCurrentLevel(root, level): if root is None: return if level == 1: print(root.data, end=' ') elif level>1: printCurrentLevel(root.left, level-1) printCurrentLevel(root.right, level-1) # Bereken de hoogte van een boom: het aantal knooppunten # langs het langste pad vanaf het hoofdknooppunt naar # het verste blad node def height(node): if node is Geen: return 0 else: # Bereken de hoogte van elke subboom lheight = height(node.left) rheight = height(node.right) # Gebruik de grotere als lheight> rheight: return lheight+1 else: return rheight+1 # Stuurprogramma om bovenstaande functie te testen als __name__ == '__main__': root = Knooppunt(1) root.left = Knooppunt(2) root.right = Knooppunt(3) root. left.left = Knooppunt(4) root.left.right = Knooppunt(5) print('Niveauvolgorde van de binaire boom is -') printLevelOrder(root) # Deze code is bijgedragen door Nikhil Kumar Singh(nickzuck_007)> C# // Recursive c# program for level // order traversal of Binary Tree using System; // Class containing left and right // child of current node and key value public class Node { public int data; public Node left, right; public Node(int item) { data = item; left = right = null; } } class GFG { // Root of the Binary Tree public Node root; public void BinaryTree() { root = null; } // Function to print level order // traversal of tree public virtual void printLevelOrder() { int h = height(root); int i; for (i = 1; i <= h; i++) { printCurrentLevel(root, i); } } // Compute the 'height' of a tree -- // the number of nodes along the longest // path from the root node down to the // farthest leaf node. public virtual int height(Node root) { if (root == null) { return 0; } else { // Compute height of each subtree int lheight = height(root.left); int rheight = height(root.right); // use the larger one if (lheight>hoogte) { return (lhoogte + 1); } anders { return (hoogte + 1); } } } // Print knooppunten op het huidige niveau public virtual void printCurrentLevel(Node root, int level) { if (root == null) { return; } if (niveau == 1) { Console.Write(root.data + ' '); } else if (niveau> 1) { printCurrentLevel(root.left, niveau - 1); printCurrentLevel(root.right, niveau - 1); } } // Stuurprogrammacode public static void Main(string[] args) { GFG tree = new GFG(); tree.root = nieuw knooppunt (1); tree.root.left = nieuw knooppunt(2); tree.root.right = nieuw knooppunt(3); tree.root.left.left = nieuw knooppunt(4); tree.root.left.right = nieuw knooppunt(5); Console.WriteLine('Niveauvolgorde doorlopen ' + 'van binaire boom is '); boom.printLevelOrder(); } } // Deze code is bijgedragen door Shrikant13> Javascript // Recursive javascript program for level // order traversal of Binary Tree // Class containing left and right child of current // node and key value class Node { constructor(val) { this.data = val; this.left = null; this.right = null; } } // Root of the Binary Tree var root= null; // Function to print level order traversal of tree function printLevelOrder() { var h = height(root); var i; for (i = 1; i <= h; i++) printCurrentLevel(root, i); } // Compute the 'height' of a tree -- the number // of nodes along the longest path // from the root node down to the farthest leaf node. function height(root) { if (root == null) return 0; else { // Compute height of each subtree var lheight = height(root.left); var rheight = height(root.right); // Use the larger one if (lheight>hoogte) retour (lhoogte + 1); anders retour (rechts + 1); } } // Print knooppunten op het huidige niveau, functie printCurrentLevel(root , level) { if (root == null) return; if (niveau == 1) console.log(root.data + ' '); else if (niveau> 1) { printCurrentLevel(root.left, niveau - 1); printCurrentLevel(root.right, niveau - 1); } } // Stuurprogramma om bovenstaande functies te testen root = new Node(1); root.left = nieuw knooppunt(2); root.right = nieuw knooppunt(3); root.left.left = nieuw knooppunt(4); root.left.right = nieuw knooppunt(5); console.log('Niveauvolgorde van de binaire boom is '); printLevelOrder(); // Deze code is bijgedragen door umadevi9616> Uitvoer
Level Order traversal of binary tree is 1 2 3 4 5>
Tijdcomplexiteit: O(N), waarbij N het aantal knooppunten in de scheve boom is.
Hulpruimte: O(1) Als de recursiestapel in aanmerking wordt genomen, is de gebruikte ruimte O(N).
extensiebestand java
Niveau Order Traversal gebruiken Wachtrij
We moeten de knooppunten op een lager niveau bezoeken voordat we een knooppunt op een hoger niveau bezoeken. Dit idee lijkt veel op dat van een wachtrij. Duw de knooppunten van een lager niveau in de wachtrij. Wanneer een knooppunt wordt bezocht, haalt u dat knooppunt uit de wachtrij en duwt u het kind van dat knooppunt in de wachtrij.
Dit zorgt ervoor dat knooppunten van een lager niveau eerder worden bezocht dan knooppunten van een hoger niveau.
Hieronder vindt u de implementatie van de bovenstaande aanpak:
C++ // C++ program to print level order traversal #include using namespace std; // A Binary Tree Node struct Node { int data; struct Node *left, *right; }; // Iterative method to find height of Binary Tree void printLevelOrder(Node* root) { // Base Case if (root == NULL) return; // Create an empty queue for level order traversal queueQ; // Zet root in de wachtrij en initialiseer de hoogte q.push(root); while (q.empty() == false) {// Druk de voorkant van de wachtrij af en verwijder deze uit de wachtrij Knooppunt* knooppunt = q.front(); uit<< node->gegevens<< ' '; q.pop(); // Enqueue left child if (node->links != NULL) q.push(knooppunt->links); // Plaats het juiste kind in de wachtrij if (node->right != NULL) q.push(node->right); } } // Hulpprogrammafunctie om een nieuw boomknooppunt te maken Node* newNode(int data) { Node* temp = new Node; temp->gegevens = gegevens; temp->links = temp->rechts = NULL; retourtemperatuur; } // Stuurprogramma om bovenstaande functies te testen int main() {// Laten we een binaire boom maken zoals weergegeven in het bovenstaande diagram Node* root = newNode(1); root->links = newNode(2); root->right = newNode(3); root->links->links = newNode(4); root->links->rechts = newNode(5); uit<< 'Level Order traversal of binary tree is
'; printLevelOrder(root); return 0; }> C // Iterative Queue based C program // to do level order traversal // of Binary Tree #include #include #define MAX_Q_SIZE 500 // A binary tree node has data, // pointer to left child // and a pointer to right child struct node { int data; struct node* left; struct node* right; }; // Function prototypes struct node** createQueue(int*, int*); void enQueue(struct node**, int*, struct node*); struct node* deQueue(struct node**, int*); // Given a binary tree, print its nodes in level order // using array for implementing queue void printLevelOrder(struct node* root) { int rear, front; struct node** queue = createQueue(&front, &rear); struct node* temp_node = root; while (temp_node) { printf('%d ', temp_node->gegevens); // Enqueue left child if (temp_node->left) enQueue(queue, &rear, temp_node->left); // Enqueue right child if (temp_node->right) enQueue(queue, &rear, temp_node->right); // Haal het knooppunt uit de wachtrij en maak het temp_node temp_node = deQueue(queue, &front); } } // Hulpprogrammafuncties struct node** createQueue(int* front, int* rear) { struct node** wachtrij = (struct node**)malloc( sizeof(struct node*) * MAX_Q_SIZE); *voor = *achter = 0; terugkeer wachtrij; } void enQueue(struct node** wachtrij, int* achter, struct node* new_node) { wachtrij[*achter] = new_node; (*achter)++; } struct node* deQueue(struct node** wachtrij, int* front) { (*front)++; retourwachtrij[*front - 1]; } // Helperfunctie die een nieuw knooppunt toewijst met de // gegeven gegevens en NULL linker- en rechteraanwijzers. struct node* newNode(int data) { struct node* node = (struct node*)malloc(sizeof(struct node)); knooppunt->gegevens = gegevens; knooppunt->links = NULL; knooppunt->rechts = NULL; terugkeer (knooppunt); } // Stuurprogramma om bovenstaande functies te testen int main() { struct node* root = newNode(1); root->links = newNode(2); root->right = newNode(3); root->links->links = newNode(4); root->links->rechts = newNode(5); printf('Niveauvolgorde door de binaire boom is
'); printLevelOrder(root); retour 0; }> Java // Iterative Queue based Java program // to do level order traversal // of Binary Tree import java.util.LinkedList; import java.util.Queue; // Class to represent Tree node class Node { int data; Node left, right; public Node(int item) { data = item; left = null; right = null; } } // Class to print Level Order Traversal class BinaryTree { Node root; // Given a binary tree. Print // its nodes in level order // using array for implementing queue void printLevelOrder() { Queuewachtrij = nieuwe LinkedList(); wachtrij.toevoegen(root); while (!queue.isEmpty()) {// poll() verwijdert het huidige hoofd. Knooppunt tempNode = wachtrij.poll(); Systeem.out.print(tempNode.data + ''); // Zet het linker kind in de wachtrij if (tempNode.left != null) { wachtrij.add(tempNode.left); } // Rechts kind in wachtrij plaatsen if (tempNode.right != null) { wachtrij.add(tempNode.right); } } } public static void main(String args[]) {// Een binaire boom maken en // de knooppunten invoeren BinaryTree tree_level = new BinaryTree(); tree_level.root = nieuw knooppunt(1); tree_level.root.left = nieuw knooppunt(2); tree_level.root.right = nieuw knooppunt(3); tree_level.root.left.left = nieuw knooppunt(4); tree_level.root.left.right = nieuw knooppunt(5); System.out.println('Niveauvolgorde van de binaire boom is - '); tree_level.printLevelOrder(); } }> Python # Python program to print level # order traversal using Queue # A node structure class Node: # A utility function to create a new node def __init__(self, key): self.data = key self.left = None self.right = None # Iterative Method to print the # height of a binary tree def printLevelOrder(root): # Base Case if root is None: return # Create an empty queue # for level order traversal queue = [] # Enqueue Root and initialize height queue.append(root) while(len(queue)>0): # Druk de voorkant van de wachtrij af en # verwijder deze uit de wachtrij print(queue[0].data, end=' ') node = wachtrij.pop(0) # Zet het linker kind in de wachtrij als node.left niet Geen is: wachtrij.append(node.left) # Plaats het rechter kind in de wachtrij als node.right niet Geen is: wachtrij.append(node.right) # Stuurprogramma om bovenstaande functie te testen als __name__ == '__main__': root = Knooppunt(1 ) root.left = Knooppunt(2) root.right = Knooppunt(3) root.left.left = Knooppunt(4) root.left.right = Knooppunt(5) print('Niveauvolgorde van de binaire boom is - ') printLevelOrder(root) # Deze code is bijgedragen door Nikhil Kumar Singh(nickzuck_007)> C# // Iterative Queue based C# program // to do level order traversal // of Binary Tree using System; using System.Collections.Generic; // Class to represent Tree node public class Node { public int data; public Node left, right; public Node(int item) { data = item; left = null; right = null; } } // Class to print Level Order Traversal public class BinaryTree { Node root; // Given a binary tree. Print // its nodes in level order using // array for implementing queue void printLevelOrder() { Queuewachtrij = nieuwe wachtrij(); wachtrij.Enqueue(root); while (queue.Count != 0) { Knooppunt tempNode = wachtrij.Dequeue(); Console.Write(tempNode.data + ''); // Enqueue left child if (tempNode.left != null) { wachtrij.Enqueue(tempNode.left); } // Rechts kind in wachtrij plaatsen if (tempNode.right != null) { wachtrij.Enqueue(tempNode.right); } } } // Stuurprogrammacode public static void Main() {// Een binaire boom maken en // de knooppunten invoeren BinaryTree tree_level = new BinaryTree(); tree_level.root = nieuw knooppunt(1); tree_level.root.left = nieuw knooppunt(2); tree_level.root.right = nieuw knooppunt(3); tree_level.root.left.left = nieuw knooppunt(4); tree_level.root.left.right = nieuw knooppunt(5); Console.WriteLine('Niveauvolgorde doorlopen ' + 'van binaire boom is - '); tree_level.printLevelOrder(); } } // Deze code is bijgedragen door PrinciRaj1992> Javascript class Node { constructor(val) { this.data = val; this.left = null; this.right = null; } } // Class to represent a deque (double-ended queue) class Deque { constructor() { this.queue = []; } // Method to add an element to the end of the queue enqueue(item) { this.queue.push(item); } // Method to remove and return the first element of the queue dequeue() { return this.queue.shift(); } // Method to check if the queue is empty isEmpty() { return this.queue.length === 0; } } // Function to perform level order traversal of a binary tree function printLevelOrder(root) { // Create a deque to store nodes for traversal const queue = new Deque(); // Add the root node to the queue queue.enqueue(root); // Continue traversal until the queue is empty while (!queue.isEmpty()) { // Remove and get the first node from the queue const tempNode = queue.dequeue(); // Print the data of the current node console.log(tempNode.data + ' '); // Enqueue the left child if it exists if (tempNode.left !== null) { queue.enqueue(tempNode.left); } // Enqueue the right child if it exists if (tempNode.right !== null) { queue.enqueue(tempNode.right); } } } // Create a binary tree and enter the nodes const root = new Node(1); root.left = new Node(2); root.right = new Node(3); root.left.left = new Node(4); root.left.right = new Node(5); // Print the level order traversal of the binary tree console.log('Level order traversal of binary tree is - '); printLevelOrder(root);> Uitvoer
Level Order traversal of binary tree is 1 2 3 4 5>
Tijdcomplexiteit: O(N) waarbij N het aantal knooppunten in de binaire boom is.
Hulpruimte: O(N) waarbij N het aantal knooppunten in de binaire boom is.